양자정보 개요
양자 충실도 (Fidelity)[편집]
양자 충실도(fidelity)란 대각합 거리(trace distance)와 더불어, 양자 상태 두 개가 얼마나 비슷한지를 정량화하는 물리량이다. 양자 상태 $$\rho,\ \ \sigma$$가 있을 때 두 상태의 양자 충실도 값은 다음과 같이 정의된다.
\[F(\rho,\sigma)= \text{tr}\sqrt{\rho^{1\text{/}2}\sigma\rho^{1\text{/}2}}\]
위의 정의는 일견 복잡해 보이지만, 빈번히 사용되는 아래 두 가지 경우에 있어 매우 간단한 형태로 표현된다.[1] 우선, 두 상태 $$\rho,\ \sigma$$가 서로 교환관계에 있는 경우 각각의 상태는 $$\rho= \sum_{i}^{}{ p_{i}\left| i \right\rangle\left\langle i \right|}$$와 $$\sigma =\sum_{i}^{}{ q_{i}\left| i \right\rangle\left\langle i \right|}$$와 같은 형태로, 특정 기저 $$\left| i \right\rangle$$에 대하여 동시에 대각화가 가능하다. 이를 양자 충실도 정의에 대입하여 계산하면 $$F(\rho,\sigma)= \sum_{i}^{}{\sqrt{p_{i}q_{i}}}$$라는 간단한 표현식을 얻을 수 있다. 더 나아가 이 경우의 양자 충실도는 확률분포 {$$p_{i}$$}와 {$$q_{i}$$} 사이의 가까운 정도를 측정하는 고전 충실도와 동일함을 알 수 있다. 양자정보이론에서 자주 고려하는 또 다른 경우는, 하나의 상태는 순수 상태로 주어지고 다른 상태가 일반적인 밀도 행렬로 주어지는 상황이다. 순수 상태와 밀도 행렬을 각각 $$\left| \psi \right\rangle$$, $$\rho$$라 할 때, 두 상태 사이의 양자 충실도는 다음과 같이 계산된다. $$F\left( \left| \psi \right\rangle,\rho \right) =\sqrt{\left\langle \psi \right|\rho\left| \psi \right\rangle}$$. 이때 양자 충실도 값은 일반적인 상태의 순수 상태에 대한 기댓값의 제곱근 형태로 표현된다. 양자 충실도는 또한 유니타리(unitary) 변환에 대하여 불변하는 성질을 갖고 있으며, 이는 임의의 유니타리(unitary) 변환 $$U$$에 대하여 다음 수식 유도를 통해 확인할 수 있다. $$F(\rho,\sigma)= F\left( U\rho U^{\dagger},U\sigma U^{\dagger} \right)$$.[1] 경우에 따라 위에 주어진 정의에서 제곱근을 씌우지 않은 값을 양자 충실도로 사용하기도 한다.
초압축 코딩 (Superdense Coding)[편집]
초압축 코딩에서는 전송자 Alice가 수신자 Bob에게 고전 정보를 전달하는 상황을 가정한다. 더 구체적으로 초압축 코딩 방식을 활용하여 단 하나의 큐비트를 양자 채널을 통해 Bob에게 전송함으로써 두 개의 고전 비트 정보를 전송할 수 있다. 한 가지 중요한 가정은 Alice와 Bob이 얽힘 상태를 공유해야 한다는 점이다. 아래 이체 상태의 첫 번째와 두 번째 상태를 Alice와 Bob이 각각 나누어 가진 상황을 가정해 보자.
\[\left| \varphi^{+} \right\rangle= \ \frac{\left| 00 \right\rangle + \left| 11 \right\rangle}{\sqrt{2}}\]
Alice가 00, 01, 10, 11의 고전 정보를 전송할 때마다 자신의 큐비트에 $$I$$, $$Z$$, $$X$$, $$iY$$의 연산을 수행한다면 최종적으로 Bob이 전달받는 상태는 아래 표와 같이 주어진다. 양자 상태 $$\left| \varphi^{+} \right\rangle$$, $$\left| \varphi^{-} \right\rangle$$, $$\left| \psi^{+} \right\rangle$$, $$\left| \psi^{-} \right\rangle$$는 벨 상태(Bell state) 또는 벨 기저(Bell basis)라 불리는 상태이다. 벨 기저는 서로 정규직교(orthonormal)하므로 이를 구분하기 위한 양자 측정을 구현할 수 있다. 따라서 Bob이 각각의 상태를 구분할 수 있는 측정을 수행해 Alice가 전달하는 2bit의 고전 정보가 무엇인지 완벽하게 구분할 수 있다.
| Alice가 전송하고자 하는 고전 정보 |
Bob이 전달받는 상태 |
|---|---|
| 00 | \[\left| \varphi^{+} \right\rangle= \ \frac{\left| 00 \right\rangle + \left| 11 \right\rangle}{\sqrt{2}}\] |
| 01 | \[\left| \varphi^{-} \right\rangle= \ \frac{\left| 00 \right\rangle - \left| 11 \right\rangle}{\sqrt{2}}\] |
| 10 | \[\left| \psi^{+} \right\rangle= \ \frac{\left| 01 \right\rangle + \left| 10 \right\rangle}{\sqrt{2}}\] |
| 11 | \[\left| \psi^{-} \right\rangle= \ \frac{\left| 01 \right\rangle - \left| 10 \right\rangle}{\sqrt{2}}\] |
양자 프로세스 토모그래피 (Quantum Process Tomography)[편집]
측정으로 붕괴되기 전 양자계의 정보를 분석하기 위해서는 실질적으로 양자 상태를 확인하는 작업이 필요하다. 양자 상태를 확인하려는 목적으로 주로 활용되는 기술로 양자 상태 토모그래피(quantum state tomography; QST) 방법이 있다. 양자 상태 앙상블에 대한 측정의 기댓값을 구함으로써 임의의 양자 상태를 확인하는 방법이다. 이와 유사하게, 양자 프로세스 토모그래피(quantum process tomography; QPT)은 물리계에 작용하는 ‘프로세스’, 즉 물리계의 시간에 따른 동역학적 변화를 확인하는 방법으로 활용된다. 수학적으로 QPT는 양자 맵(map)을 확인하는 것을 말한다.
QPT는 QST의 필요 여부에 따라 크게 간접 QPT, 직접 QPT로 구분된다. 간접 QPT에서는 변화를 확인하고자 하는 물리계 외의 추가적인 양자 물리계의 변화에 대한 정보를 매핑한 후 QST를 활용하여 변화에 대한 정보를 복원한다. 간접 QPT에서는 복원 시에 결과 상태에 역매핑(inversion mapping)을 적용해주는 과정이 필수적이다.[2] 간접 QPT 방식의 예로, SQPT(standard QPT), AAPT(ancilla-assisted QPT)가 있다. 반면, 직접 QPT에서는 상태 토모그래피 방법을 적용할 필요 없이 실험상 측정값을 통해 동역학적 정보를 구한다. DCQD(direct characterization of quantum dynamics)는 양자 상태 토모그래피 기법 없이 최초로 제안된 직접 QPT 방식이다. 직접 QPT 방식을 기반하여 물리계의 비고전성질 확인[3], 양자 프로세스에서 평균 충실도 측정[4] 등에 활용하기 위한 연구가 진행된 바 있다. 2018년에는 연속적인 약한 측정을 통해 실험적으로 직접 QPT 방식을 구현한 연구가 보고되었다.[5]
엔트로피 (Entropy)[편집]
정보이론에서 엔트로피는 정보의 정량화 함수로 활용되며, 양자정보의 근간이 되는 개념 중 하나이다. 고전 확률분포 사이의 정보를 정량화할 때 주로 사용되는 것은 섀넌 엔트로피(Shannon entropy)이다. 섀넌 엔트로피는 어떤 무작위 측정 $$A$$가 존재할 때, 측정 후 얻을 수 있는 정보를 정량화 한다. 측정값 {$$a$$}에 대하여 측정 확률분포가 {$$p_{a}$$}로 주어지는 무작위 측정 $$A$$가 존재한다고 가정하자. 이 때 섀넌 엔트로피는 다음과 같이 정의된다. 여기에서, 정보를 비트 단위로 계산하기 때문에, 로그함수의 밑을 흔히 2로 한다.
\[H(A)= - \sum_{a}^{}{ p_{a}\log p_{a}}\]
위에서 엔트로피는 음의 로그 함수의 기댓값 형태로 정의된 것을 알 수 있다. 어떤 확률 $$p$$의 음의 로그 $$- \log p$$는 확률이 낮을수록, 다시 말해 정보의 예측 불가능성이 높을수록 큰 값을 갖는다. 또한 로그 형태 표현을 통해 정보량을 표현하면, 두 개 확률 $$p$$, $$q$$의 곱에 해당하는 정보량을 각각의 정보량의 합으로 표현할 수 있다. $$- \log{pq}= - \log p - \log q$$. 이런 관점에서 무작위하게 측정값이 주어지는 측정의 섀넌 엔트로피는 각각의 측정값에 해당하는 정보량 또는 무작위도의 평균값으로 이해할 수 있다. 기본적인 엔트로피 표현 형태로, 이항 엔트로피(binary entropy), 상대 엔트로피(relative entropy), 결합 엔트로피(joint entropy), 조건부 엔트로피(conditional entropy)가 있다. 이항 엔트로피는 측정값의 확률분포가 두 가지 확률 $$p$$, $$1 - p$$로 주어지는 경우에 대한 엔트로피로서 다음과 같이 정의된다.
\[H_{\text{bin}}(p)= - p\log p - (1 - p)\log(1 - p)\]
이항 엔트로피는 $$H(p)= H(1 - p)$$의 관계가 성립하는 $$p =1\text{/}2$$에 대한 대칭 함수이며, $$p= 1\text{/}2$$인 경우에 그 최댓값 1을 갖는다. 상대 엔트로피는 같은 변수 $$a$$에 대한 두 개 확률 분포 {$$p_{a}$$}와 {$$q_{a}$$}의 가까운 정도를 정량화하는 데 유용한 함수이다.[1] 두 확률분포에 대한 상대 엔트로피는 다음과 같이 정의된다.
\[H(p_{a}||q_{a}) =\sum_{a}^{}{p_{a}\log\frac{p_{a}}{q_{a}}}= - H(A) - \sum_{a}^{}{ p_{a}\log q_{a}}\]
결합 엔트로피와 조건부 엔트로피는 두 개의 무작위 측정값을 갖는 측정 $$A,\ B$$가 주어질 때의 엔트로피이다. 두 측정의 결합 확률분포를 $$p(a,\ b)$$로 주어질 때, 결합 엔트로피 $$H(A,B)$$와 조건부 엔트로피 $$H(A|B)$$는 다음과 같은 형태로 정의된다.
\[{H(A,B)= - \sum_{a,b}^{}{ p(a,b)\log{p(a,b)}}}\] \[{H(A|B)= H(A,B) - H(B)}\]
위 식 아래에 있는 조건부 엔트로피 $$H(A|B)$$는 $$B$$의 측정결과를 알고 있을 때 $$A$$의 측정결과가 얼마나 무작위한지를 평균적으로 정량화하는 값이다.
섀넌 엔트로피는 고전적인 확률분포가 주어질 때 측정값의 무작위도를 정량화 한다. 이러한 정량화 방식을 확률분포가 아니라 밀도 연산자에 대해 적용하여, 밀도 연산자에 대한 엔트로피를 생각할 수 있는데, 이를 처음 제안한 물리학자의 이름을 따 폰 노이만 엔트로피(Von Neumann entropy)라 부르며, 다음과 같이 정의한다.
\[S(\rho)= - \text{tr}\left( \rho\log\rho \right) =- \lambda_{a}\log\lambda_{a}\]
위 식 끝에 있는 표현식은 밀도 행렬의 고유값 $$\lambda_{a}$$의 함수로 표현한 식이다. 폰 노이만 엔트로피는 다음과 같은 기본 성질을 갖는다.
1) 엔트로피는 0 이상의 값을 가지며, 순수 상태인 경우에만 필요충분적으로 엔트로피가 0값을 갖는다.
2) $$d$$차원 힐베르트 공간에서 엔트로피는 최대 $$\log d$$ 값을 가진다. 상태가 최대 혼합 상태에 있는 경우에만 필요충분적으로 $$\log d$$ 값을 갖는다.
3) 합성 물리계(composite system) $$A$$와 $$B$$가 순수 상태에 있을 때, 다음이 성립한다. $$S(A)= S(B)$$.[1]
LOCC (Local Operations and Classical Communication)[편집]
양자정보이론의 중요한 문제 중 하나는 이른바 얽힘 증류(entanglement distillation)를 통해 주어진 상태의 양자 얽힘 정도를 높이는 것이다. 이를 위해서는 비국소 측정을 통해 높은 얽힘 상태를 만드는 방법과 국소 측정과 측정 결과에 대한 고전 통신만을 활용하여 얽힘을 증류하는 방법이 있다. 후자의 방법에서 국소 측정과 고전 통신을 활용하는 방식을 LOCC(local operations and classical communication)라 부른다. LOCC는 양자 연산의 핵심적인 기술인 오류 수정에도 중요한 역할을 하므로 아래 간단한 상태 구분 예를 통해 LOCC 개념을 소개한다.
Alice와 Bob이 얽힘 상태를 공유하고 있고 두 개의 벨 상태 $$\left| \varphi^{+} \right\rangle= \left( \left| 00 \right\rangle + \left| 11 \right\rangle \right)\text{/}\sqrt{2}$$, $$\left| \psi^{+} \right\rangle =\left( \left| 01 \right\rangle + \left| 10 \right\rangle \right)\text{/}\sqrt{2}$$ 중 어떤 상태에 있는지 구분해야 하는 상황을 가정하자. 이 때, Alice와 Bob이 서로 통신을 사용하지 않고 각자의 국소 측정 통계만 확인한다고 하면, 두 개의 상태 중 어떤 상태에 있는지 확인할 수 없다. 두 상태 모두에서 국소 측정을 수행한 결과는 0, 1이 1/2의 확률로 동일하게 나오기 때문이다. 이 때, Alice와 Bob이 자신의 국소 측정 결과를 고전 통신을 통해 교환한다면 어떤 상태에 있는지 구분 가능하다. 예를 들어 고전 통신 결과 Alice와 Bob이 서로 다른 측정값이 나온 것으로 확인되었다면, $$\left| \varphi^{+} \right\rangle$$ 상태에 존재할 수 없으므로, 둘이 공유하는 상태는 $$\left| \psi^{+} \right\rangle$$인 것으로 확인 가능하다. 이상의 예는 LOCC를 얽힘 상태를 구분하는 목적으로 사용한 하나의 예가 된다.
양자 이점, 양자 우위 (Quantum Advantage, Quantum Supremacy)[편집]

양자 우위(quantum supremacy; QS)는 양자 연산을 통하여 어떠한 고전 컴퓨터로도 실현 불가능한 연산 능력에 도달한 것을 의미한다. 양자 컴퓨터가 고전 컴퓨터를 능가하는 연산 수행 능력을 보여주는 것을 의미하는 양자 이점(quantum advantage; QA)과 구분이 필요한 경우 구분하여 지칭하도록 한다.
양자 우위를 보이는 것은 물리 이론에 근본적인 중요성을 갖는 것을 넘어서, 실용적 차원에서도 그 결과가 미칠 영향이 큰 연구 분야이다. 양자 우위가 실현될 경우 고전 컴퓨터가 다항 시간 내에 어떠한 물리 과정도 구현할 수 있다는 이른바 ‘확장된 Church-Turing 명제’를 반박하는 결과를 가져올 것이다.[6] 따라서 얽힘과 같은 현상을 직접적으로 이용하지 않고 ‘연산’ 차원에서 양자역학의 중요성을 증명하는 결과를 가져올 것이다. 한 가지 유의할 점은, 우위를 보이는 데에 특별히 실용적으로 유용한 문제를 고려할 필요는 없다는 데 있다. 이에 Preskill이 NISQ(noisy intermediate-scale quantum) 논문에서 제안한 바와 같이 단순히 양자 우위를 보이는 문제뿐 아니라, 실용적으로 쓸모 있는 문제에 대한 연구에 대한 관심도 병행되어야 할 것이다.[7]
양자 우위는 단순히 양자 컴퓨터의 높은 연산 능력을 보여야 하는 것이 아니라 고전 컴퓨터의 연산이 불가능한 영역에서 양자 연산이 가능함을 보여야 하므로 다른 연산 알고리듬 문제와 구별된다. 고전 연산이 불가능함을 엄밀히 증명하기 위해서는 복잡도 이론이 필요하나, 현재 단계의 복잡도 이론으로는 무조건적인 연산 불가능성을 증명할 수는 없으며, 몇 가지 가정하에 불가능성을 증명한다. 이 때, 가능한 한 약한 가정만으로도 이를 보일 수 있는 문제들이 양자 우위를 구현하기 위한 후보가 되고 있다. 예컨대 인수분해 문제, 양자 시뮬레이터 기술 등은 현재 기술 단계에서 고전 컴퓨터로 풀 수 없을 정도로 복잡한 문제라는 사실을 증명하는 것이 쉽지 않으므로 양자 우위 구현 후보가 되지 못한다.[6] 인수분해 문제의 경우 1990년에 와서야 현존하는 가장 나은 고전 알고리듬이 제안되었으며, 더 개선될 여지가 있다. 양자 시뮬레이터 또한 시뮬레이터에 영향을 미치는 온도, 커플링 상수 등의 다양한 변수로 인해 복잡도를 계산하기 어려우며, 고전 컴퓨터로 연산 불가능성을 증명하기 어려운 문제가 있다.
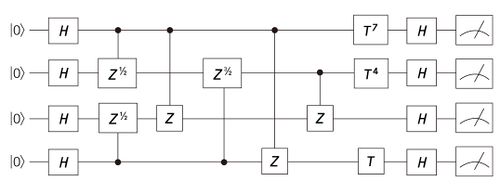
따라서 현대 양자 컴퓨터는 보손 샘플링(boson sampling) 또는 무작위 양자 회로(random quantum circuit) 등의 플랫폼을 주로 활용한다. 이 플랫폼들의 연산 목적을 이해하기 위해서는 샘플링이 무엇인지 우선 알아야 한다. 샘플링이란 결정론적으로 답을 구하는 것이 아니라, 주어진 확률분포에서 원하는 샘플을 얻는 것을 말한다. 보손 샘플링에서는 보손 입자인 단일 광자들을 선형 광학 네트워크 장치에 통과시켜 나오는 신호의 확률분포를 샘플링 한다. 보손 샘플링이 되는 확률분포는 고전적으로는 샘플링하기 어렵다는 것이 이른바 ‘다항 위계(polynomial hierachy)’ 가정을 포함한 복잡도 이론을 통해 알려져 있다.[6] 무작위 양자 회로는 표준적인 양자 회로와 양자 게이트를 활용하는 양자 우위 구현 모델이다. 무작위 양자 회로에서는 고정된 양자 입력 상태로부터 측정값들을 샘플링한다. 이때, 측정 전의 양자 게이트들이 서로 교환관계에 있는지 여부를 통해 무작위 양자 회로의 종류를 구분한다. 위의 두 그림은 각각 보손 샘플링과 교환 양자회로의 간단한 예를 보여준다.
2019년 구글에서 무작위 양자 회로 방식을 통해 이차원 평면에 53개의 초전도 큐비트를 배열하는 실험을 수행한 결과 양자 우위에 해당하는 결과를 최초로 얻음을 주장하였다.[8] 구글 연구진은 제안한 양자 회로를 통해 고전 컴퓨터로 10,000년이 걸리는 문제를 200초 만에 해결하였다고 주장하였다. IBM 연구소 연구진들은 구글에서 고전 컴퓨터 연산 시 충분한 메모리를 고려하지 않았으며, 메모리를 충분히 고려할 시 해당 연산을 수일 내 풀 수 있을 것이라고 이의를 제기한 바 있다.[9] 이는 구글의 결과가 QS에 해당하는 결과라는 데 반론을 제기한 것으로 해석할 수 있다. 구글의 결과가 QS 또는 QA 인지를 논외로 하더라도, 구글에서 50개 이상의 큐비트 연산을 통해 NISQ 기술 영역에 도입한 연구결과를 도출했다는 데는 이의의 여지가 없을 것으로 보인다.
참고 문헌[편집]
- ↑ 이동: 1.0 1.1 1.2 1.3 M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information (Cambridge University Press, 2002)
- ↑ M. Mohseni, A. T. Rezakhani, and D. A. Lidar, Quantum-process tomography: resource analysis of different strategies, Physical Review A 77, 032322 (2008). doi:10.1103/PhysRevA.77.032322.
- ↑ P. Horodecki et al., Direct detection of quantum entanglement, in Proceedings of The Physics of Communication, 621 (2003). doi:10.1142/9789812704634_0043.
- ↑ H. F. Hofmann, Complementary classical fidelities as an efficient criterion for the evaluation of experimentally realized quantum operations, Physical Review Letters 94, 160504 (2005). doi:10.1103/PhysRevLett.94.160504.
- ↑ Y. Kim et al., Direct quantum process tomography via measuring sequential weak values of incompatible observables, Nature Communications 9, 192 (2018). doi:10.1038/s41467-018-03305-w.
- ↑ 이동: 6.0 6.1 6.2 6.3 6.4 A. W. Harrow and A. Montanaro, Quantum computational supremacy, Nature 549, 203 (2017). doi:10.1038/nature23458.
- ↑ J. Preskill, Quantum computing in the NISQ era and beyond, Quantum 2, 79 (2018). doi:10.22331/q-2018-08-06-79.
- ↑ F. Arute et al., Quantum supremacy using a programmable superconducting processor, Nature 574, 505 (2019). doi:10.1038/s41586-019-1666-5.
- ↑ https://www.ibm.com/blogs/research/2019/10/on-quantum-supremacy