반도체 기반: 두 판 사이의 차이
(→개발 현황) |
|||
| (사용자 4명의 중간 판 60개는 보이지 않습니다) | |||
| 12번째 줄: | 12번째 줄: | ||
== 색중심의 종류== | == 색중심의 종류== | ||
결정에 존재하는 단일 불순물(impurity), 공동 (vacancy) 등과 같은 점 결함(point defect)은 고체 내 속박된 인공 원자로서, 스핀 및 광학 [[큐비트]]를 고체 시스템에서 생성하는 중요한 역할을 한다. 대표적인 점결함 예인 Nitrogen-Vacancy (NV) 색중심은 다이아몬드의 결정격자에서 탄소원자가 제거되어 생성된 공극에 질소원자가 결합하고 인접한 격자에서 하나의 탄소가 빠져 비어있는 상태인 점결함이다. NV 색중심은 중성(NV<sup>0</sup>)또는 음성(NV<sup>-</sup>)을 띌 수 있다. 음성을 띌 때 총 두 개의 홀전자(탄소와 공극에서 각각 하나씩)를 가지며 바닥상태(ground state)에서 스핀 삼중항(triplet) | 결정에 존재하는 단일 불순물(impurity), 공동 (vacancy) 등과 같은 점 결함(point defect)은 고체 내 속박된 인공 원자로서, 스핀 및 광학 [[큐비트]]를 고체 시스템에서 생성하는 중요한 역할을 한다. 대표적인 점결함 예인 Nitrogen-Vacancy (NV) 색중심은 다이아몬드의 결정격자에서 탄소원자가 제거되어 생성된 공극에 질소원자가 결합하고 인접한 격자에서 하나의 탄소가 빠져 비어있는 상태인 점결함이다. NV 색중심은 중성(NV<sup>0</sup>)또는 음성(NV<sup>-</sup>)을 띌 수 있다. 음성을 띌 때 총 두 개의 홀전자(탄소와 공극에서 각각 하나씩)를 가지며 바닥상태(ground state)에서 스핀 삼중항 상태(triplet state)(S=1)인 스핀 [[큐비트]]가 된다. 이러한 결정 내 색중심은 다이아몬드 내에서도 Silicon vacancy (SiV), Germanium vacancy (GeV) 등 다양한 형태로 존재할 수 있고, 다이아몬드 외에도 SiC, GaN, h-BN 등과 같은 다양한 결정에서 연구되고 있다. | ||
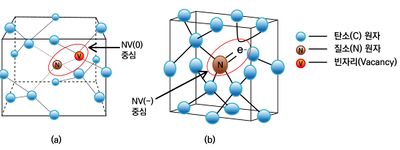
[[File: | [[File:기술백서 전체수정_68.jpg|none|thumb|400px| (a) 중성 상태의 다이아몬드 질소-공공 결함(NV<sup>0</sup> center) 와 (b) 음성 상태의 다이아몬드 질소-공동 센터(NV<sup>-</sup> center).<ref name=Haque>A. Haque and S. Sumaiya, An overview on the formation and processing of nitrogen-vacancy photonic centers in diamond by ion implantation, Journal of Manufacturing and Materials Processing <b>1</b>, 1 (2017).doi:https://doi.org/10.3390/jmmp1010006</ref> 참고문헌[1]의 그림을 재구성함. | ||
]] | ]] | ||
== NV 색중심의 에너지 준위와 스핀 구조 == | == NV 색중심의 에너지 준위와 스핀 구조 == | ||
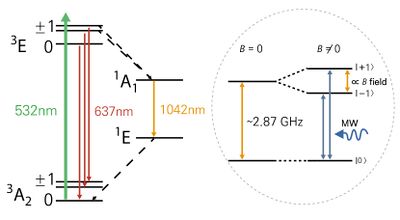
NV 색중심의 에너지 준위는 다이아몬드의 넓은 전도띠(conduction band)와 원자가띠(valence band) 간격 내 깊은 곳에 위치해있다. | NV 색중심의 에너지 준위는 다이아몬드의 넓은 전도띠(conduction band)와 원자가띠(valence band) 간격 내 깊은 곳에 위치해있다. 아래 그림은 NV 색중심의 삼중항 상태(triplet state)를 갖는 전자 스핀 (S=1)의 에너지 준위를 나타내고 있다. 외부 자기장이 없는 환경에서 m<sub>s</sub>=±1 인 상태와 m<sub>s</sub>=0 인 상태는 2.87 GHz 의 무자기장 쪼개짐(zero-field splitting)을 갖는다. NV 색중심의 전자 스핀은 삼중항 상태(<sup>3</sup>A<sub>2</sub>, <sup>3</sup>E)와 함께 단일항 상태(singlet state)(<sup>1</sup>A<sub>1</sub>, <sup>1</sup>E)에도 존재할 수 있고, 삼중항 상태에서 단일항 상태로의 전이(transition) 또한 가능하다. | ||
[[File: | [[File:기술백서 전체수정_69.jpg|none|thumb|right|400px| 다이아몬드 질소-공공 결함(NV 색중심)의 에너지 준위 다이어그램.<ref name=Lee>M. Lee, J. Yoon, and D. Lee,Magnetometers-Fundamentals and Applications of Magnetism(intechOpen, 2019)doi:https://dx.doi.org/10.5772/intechopen.75335.</ref> 참고문헌[2]의 그림을 재구성함. | ||
]] | ]] | ||
== NV 색중심의 전자 스핀 [[큐비트]] 구동원리 == | == NV 색중심의 전자 스핀 [[큐비트]] 구동원리 == | ||
NV 색중심 전자 스핀은 | NV 색중심 전자 스핀은 에너지 준위를 기반, 레이저 광펌핑, 마이크로파, 발광을 이용하여 스핀 [[큐비트]]의 초기화, 제어, 측정이 가능하다. 실질적으로는 바닥 삼중항 상태의 전자 스핀을 이준위 큐비트 시스템으로 사용하게 되는데 m<sub>s</sub>=0 스핀 상태를 큐비트의 |0> 으로 m<sub>s</sub>=±1 스핀 상태 중 하나를 큐비트의 |1> 로 사용가능하다. 축퇴(degeneracy)되어 있는 m<sub>s</sub>=±1 스핀상태는 외부자기장을 인가하는 경우 축퇴상태가 쪼깨지게 되어 각 스핀 상태를 선택적으로 접근할 수 있다. | ||
<b>초기화(initialization)</b> | <b>초기화(initialization)</b> | ||
바닥 삼중항 상태(<sup>3</sup>A<sub>2</sub>)의 전자는 가시광 파장 (532 nm)의 레이저를 가하는 경우 스핀이 보존되는 들뜬 삼중항 상태(<sup>3</sup>E)로 여기된다. 이때 <sup>3</sup>E의 m<sub>s</sub>=0 상태의 전자는 원래의 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0 상태로 떨어지며 가시광 빛(637 nm)을 방출한다. 반면 <sup>3</sup>E의 m<sub>s</sub>=±1로 여기된 전자는 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=±1상태로 직접 떨어지거나 30% 정도의 확률로 singlet state 인 <sup>1</sup>A를 거쳐 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0로 떨어지게 된다. 따라서, 전자를 여기시키는 과정을 반복하면 결국 모든 전자들이 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0에 있게되어, 전자 스핀 큐비트를 |0>으로 초기화 시킬 수 있다. | 바닥 삼중항 상태(<sup>3</sup>A<sub>2</sub>)의 전자는 가시광 파장 (532 nm)의 레이저를 가하는 경우 스핀이 보존되는 들뜬 삼중항 상태(<sup>3</sup>E)로 여기된다. 이때 <sup>3</sup>E의 m<sub>s</sub>=0 상태의 전자는 원래의 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0 상태로 떨어지며 가시광 빛(637 nm)을 방출한다. 반면 <sup>3</sup>E의 m<sub>s</sub>=±1로 여기된 전자는 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=±1상태로 직접 떨어지거나 30% 정도의 확률로 단일항 상태(singlet state)인 <sup>1</sup>A를 거쳐 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0로 떨어지게 된다. 따라서, 전자를 여기시키는 과정을 반복하면 결국 모든 전자들이 <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0에 있게되어, 전자 스핀 큐비트를 |0>으로 초기화 시킬 수 있다. | ||
<b>제어(manipulation)</b> | <b>제어(manipulation)</b> | ||
m<sub>s</sub>=0로 초기화된 스핀은 2.87 GHz 정도 크기의 마이크로파를 이용하여 m<sub>s</sub>=±1 여기시킬 수 있다. 이때, 쪼개짐 간격과 정확히 일치하는(resonant) 마이크로파 (rotation pulse)를 인가하게 되면 스핀 상태가 마이크파의 인가 펄스 폭에 대한 [[공통 기술#라비 진동 (Rabi Oscillation)|라비 진동 (Rabi | m<sub>s</sub>=0로 초기화된 스핀은 2.87 GHz 정도 크기의 마이크로파를 이용하여 m<sub>s</sub>=±1 여기시킬 수 있다. 이때, 쪼개짐 간격과 정확히 일치하는(resonant) 마이크로파 (rotation pulse)를 인가하게 되면 스핀 상태가 마이크파의 인가 펄스 폭에 대한 [[공통 기술#라비 진동 (Rabi Oscillation)|라비 진동 (Rabi oscillation)]]을 하게 되고 이를 통해 이준위 전자 스핀에 대한 결맞음 제어가 가능하다. | ||
<b>측정(readout)</b> | <b>측정(readout)</b> | ||
NV 색중심 전자 스핀 상태의 측정은 공초점 현미경 기반의 광측정자기공명 (optically detected magnetic resonance,(ODMR)) 실험을 통해 이뤄진다. 스핀 초기화 과정과 마찬가지로 가시광 레이저를 이용하여 전자를 여기시키게 되면, <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0 스핀 상태의 경우, triplet state (<sup>3</sup>E의 m<sub>s</sub>=0) 사이에서만 직접 여기와 직접 천이 과정을 거치게 되지만, m<sub>s</sub>=±1 스핀 상태의 경우, singlet | NV 색중심 전자 스핀 상태의 측정은 공초점 현미경 기반의 광측정자기공명 (optically detected magnetic resonance,(ODMR)) 실험을 통해 이뤄진다. 스핀 초기화 과정과 마찬가지로 가시광 레이저를 이용하여 전자를 여기시키게 되면, <sup>3</sup>A<sub>2</sub>의 m<sub>s</sub>=0 스핀 상태의 경우, 삼중항 상태(triplet state) (<sup>3</sup>E의 m<sub>s</sub>=0) 사이에서만 직접 여기와 직접 천이 과정을 거치게 되지만, m<sub>s</sub>=±1 스핀 상태의 경우, 단일항 상태(singlet state)로의 부분천이가 발생하여, 직접 천이 파장에 해당하는 637 nm 근처의 광신호 세기를 비교 시, 스핀 상태에 따라 발광 세기에 차이가 발생된다. 이를 통해 전자 스핀이 어떠한 상태에 있는지 정보를 얻게 된다. | ||
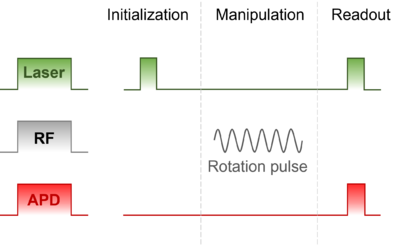
[[File:Qubit manipulation.png|none|thumb|400px| | [[File:Qubit manipulation.png|none|thumb|400px|다이아몬드 NV 색중심의 전자 스핀에 대한 초기화, 제어, 측정 과정 개념도]] | ||
== 다이아몬드의 스핀 큐비트를 이용한 [[양자 게이트]] 구현과 광자를 이용한 네트워크 형성 == | == 다이아몬드의 스핀 큐비트를 이용한 [[양자 게이트]] 구현과 광자를 이용한 네트워크 형성 == | ||
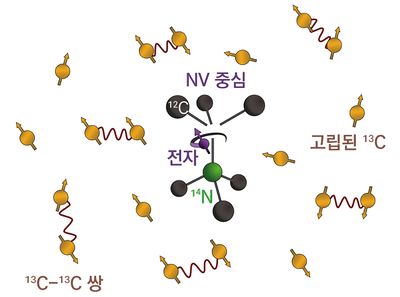
다이아몬드의 1.1%는 스핀 1/2 시스템인 <sup>13</sup>C로 이루어지고 나머지는 모두 스핀이 없는 <sup>12</sup>C로 이루어진다. 따라서 NV 색중심 근처에 <sup>13</sup>C 원자가 존재하게 되면, 전자 스핀과 핵 스핀 간 서로 상호작용을 하게된다. 우선 전자 스핀 주위에 존재하는 핵 스핀은 전자스핀에 영향을 주기 때문에 결어긋남(decoherence)을 일으키는 주원인으로 작용한다. 이러한 전자 스핀에 형향을 주는 주위환경과의 DC/AC 노이즈를 제거하기 위하여 RF 펄스를 이용한 [[공통 기술#스핀 메아리 ( | 다이아몬드의 1.1%는 스핀 1/2 시스템인 <sup>13</sup>C로 이루어지고 나머지는 모두 스핀이 없는 <sup>12</sup>C로 이루어진다. 따라서 NV 색중심 근처에 <sup>13</sup>C 원자가 존재하게 되면, 전자 스핀과 핵 스핀 간 서로 상호작용을 하게된다. 우선 전자 스핀 주위에 존재하는 핵 스핀은 전자스핀에 영향을 주기 때문에 결어긋남(decoherence)을 일으키는 주원인으로 작용한다. 이러한 전자 스핀에 형향을 주는 주위환경과의 DC/AC 노이즈를 제거하기 위하여 RF 펄스를 이용한 [[공통 기술#스핀 메아리 (spin echo)|스핀 메아리 (spin echo)]]와 [[양자 센서#동적 디커플링 (Dynamical Decoupling)|동적 디커플링 (dynamical decoupling)]] 방법 등을 사용할 수 있고, 다이아몬드 내 <sup>13</sup>C 원자 생성이 억제된 성장기술 등을 이용 전자 스핀의 결맞음 시간을 늘려주기도 한다.<ref name=Balasubramanian> G. Balasubramanian et al., Ultralong spin coherence time in isotopically engineered diamond, Nature materials <b>8</b>, 383 (2009).https://doi.org/10.1038/nmat2420.</ref> | ||
반면, 탄소의 핵 스핀도 하나의 [[큐비트]]로 사용할 수 있어, 핵스핀과 전자 스핀간의 상호작용을 잘 활용하게 되면 전자 스핀을 이용하여 인접 핵 스핀의 상태를 제어하는 것이 가능하여 [[양자 게이트(quantum gate)]] 구현이 가능해진다. 전자 스핀 하나와 핵 스핀 하나를 기반으로 한 controlled-NOT (CNOT)를 이용하게 되면 NV 색중심 주변의 탄소 핵 스핀을 컨트롤할 수 있고, 이를 이용하여, 전자 스핀 정보를 핵스핀에 긴 시간동안 저장하는 것 또한 가능하다.<ref name=Childress> L.Childress et al.,Coherent dynamics of coupled electron and nuclear spin qubits in diamond, Science <b>314</b>, 281(2006).</ref> | 반면, 탄소의 핵 스핀도 하나의 [[큐비트]]로 사용할 수 있어, 핵스핀과 전자 스핀간의 상호작용을 잘 활용하게 되면 전자 스핀을 이용하여 인접 핵 스핀의 상태를 제어하는 것이 가능하여 [[양자 게이트(quantum gate)]] 구현이 가능해진다. 전자 스핀 하나와 핵 스핀 하나를 기반으로 한 controlled-NOT (CNOT)를 이용하게 되면 NV 색중심 주변의 탄소 핵 스핀을 컨트롤할 수 있고, 이를 이용하여, 전자 스핀 정보를 핵스핀에 긴 시간동안 저장하는 것 또한 가능하다.<ref name=Childress> L.Childress et al.,Coherent dynamics of coupled electron and nuclear spin qubits in diamond, Science <b>314</b>, 281 (2006).doi:10.1126/science.1131871.</ref> | ||
다수 스핀 큐비트 간 원거리 양자 얽힘을 구현하는 방법으로는 NV 색중심의 에너지 준위간 천이에 의해 방출되는 광자를 이용하는 방법이다. 색중심의 스핀 정보는 방출 광자의 편광 등에 저장이 되는데, 서로 떨어져 있는 스핀 큐비트에서 방출 된 광자 간 양자 간섭 등을 수행하게 되면, 원거리 스핀 큐비트 간 [[양자 얽힘(quantum entanglement)]] 구현이 가능하여 [[양자 네트워크]] 로써 확장이 가능하다.<ref name=Bernien>H. Bernien et al., Heralded entanglement between solid-state qubits separated by three metres, Nature<b>497</b>, 86(2013).</ref> | 다수 스핀 큐비트 간 원거리 양자 얽힘을 구현하는 방법으로는 NV 색중심의 에너지 준위간 천이에 의해 방출되는 광자를 이용하는 방법이다. 색중심의 스핀 정보는 방출 광자의 편광 등에 저장이 되는데, 서로 떨어져 있는 스핀 큐비트에서 방출 된 광자 간 양자 간섭 등을 수행하게 되면, 원거리 스핀 큐비트 간 [[양자 얽힘(quantum entanglement)]] 구현이 가능하여 [[양자 네트워크]] 로써 확장이 가능하다.<ref name=Bernien>H. Bernien et al., Heralded entanglement between solid-state qubits separated by three metres, Nature <b>497</b>, 86 (2013).https://doi.org/10.1038/nature12016.</ref> | ||
== 개발 현황 == | == 개발 현황 == | ||
[[File: | [[File:기술백서 전체수정_91.jpg|none|thumb|400px|다이아몬드 내부의 탄소 13으로 둘러싸인 NV 색중심의 모습<ref name=Abobeih> M. H. Abobeih et al., One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment, Nature Communications <b>9</b>, 2552 (2018).https://doi.org/10.1038/s41467-018-04916-z.</ref> 참고문헌[6]의 그림을 재구성함.]] | ||
결정 내 색중심을 이용한 큐비트로는 다이아몬드 내에 NV 색중심을 이용한 큐비트가 대표적이다. 2018년 NV중심으로 [[양자역학 개요#결맞음 (Coherence)|결맞음 시간]](T<sub>1</sub>)이 1시간에 달하는 큐비트가 만들어졌다.<ref name=Abobeih>M. H. Abobeih et al., One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment, Nature Communications<b>9</b>, 2552 (2018).</ref> | 결정 내 색중심을 이용한 큐비트로는 다이아몬드 내에 NV 색중심을 이용한 큐비트가 대표적이다. 2018년 NV중심으로 [[양자역학 개요#결맞음 (Coherence)|결맞음 시간]](T<sub>1</sub>)이 1시간에 달하는 큐비트가 만들어졌다.<ref name=Abobeih>M. H. Abobeih et al., One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment, Nature Communications <b>9</b>, 2552 (2018).</ref> | ||
NV 색중심의 전자 스핀 하나와 주위 핵스핀 9개가 서로 연결되어 얽힘상태 구현이 가능한 10 큐비트 레지스터가 구현되어 확장성에 대한 가능성을 보여주기도 하였다. <ref name=Bradley>C. E Bradley et al., A ten-qubit solid-state spin register with quantum memory up to one minute, Physical Review X<b>9</b>, 031045(2019).</ref> | NV 색중심의 전자 스핀 하나와 주위 핵스핀 9개가 서로 연결되어 얽힘상태 구현이 가능한 10 큐비트 레지스터가 구현되어 확장성에 대한 가능성을 보여주기도 하였다. <ref name=Bradley>C. E Bradley et al., A ten-qubit solid-state spin register with quantum memory up to one minute, Physical Review X <b>9</b>, 031045 (2019).https://doi.org/10.1103/PhysRevX.9.031045.</ref> | ||
[[ 분류:NV 중심 | ]] | [[ 분류:NV 중심 | ]] | ||
| 59번째 줄: | 59번째 줄: | ||
== 반도체 양자점 생성 원리== | == 반도체 양자점 생성 원리== | ||
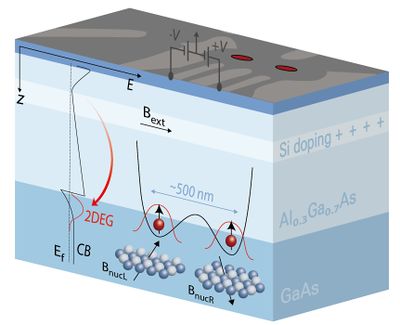
반도체 양자점은 인공 원자(artificial atom) 라고도 하며 반도체 내에서 양자점을 형성하는 게이트를 제작하여 개별 전자를 포획한뒤 게이트 전위 차 등을 이용하여 전기적으로 포획 전자의 양자 상태를 결맞음 제어할 수 있다. 양자점에 전자가 갇히면 포획 전자들의 교환(exchange) 상호작용, 전하 (charge), 스핀 (spin) 등을 [[큐비트]]로 이용할 수 있다.<ref name=mani2> | 반도체 양자점은 인공 원자(artificial atom) 라고도 하며 반도체 내에서 양자점을 형성하는 게이트를 제작하여 개별 전자를 포획한뒤 게이트 전위 차 등을 이용하여 전기적으로 포획 전자의 양자 상태를 결맞음 제어할 수 있다. 양자점에 전자가 갇히면 포획 전자들의 교환(exchange) 상호작용, 전하 (charge), 스핀 (spin) 등을 [[큐비트]]로 이용할 수 있다.<ref name=mani2>X. Zhang et al., Semiconductor quantum computation. National Science Review, <b>6</b>, 32-54 (2019).https://doi.org/10.1093/nsr/nwy153.</ref> 가장 많이 사용되는 소재는 GaAs/AlGaAs, Si/SiGe 와 같은 이종구조(heterostructure)이다. 특히, GaAs/AlGaAs 이종구조는 전자이동도가 높은 특성을 가지고 있어 제일 먼저 양자점 기반의 큐비트를 만드는데 사용되었다.<ref name=Zhang>X. Zhang et al., Qubits based on semiconductor quantum dots, Chinese Physics B, <b>27</b> 020305 (2018). doi:10.1088/1674-1056/27/2/020305/meta.</ref> 반도체 이종 구조의 접합 계면에서는 이차원 전자 가스(two-dimensional electron gas (2DEG))가 생성된다. 형성된 이차원 전자 가스층은 전자를 수직방향으로 구속하는 효과와 함께 전자를 공급하는 저장고(reservoir) 역할을 한다. 추가적으로 반도체 웨이퍼에 게이트(gate) 역할을 하는 금속 패턴을 형성 후, 음의 전위를 갖는 양자우물에 전자를 수평 방향으로 포획한다. 이로써, 3차원으로 포획된 반도체 양자점이 생성이 가능하다. 각 게이트의 전위를 조절하여 양자점 내 전자를 이동하거나 양자 상태를 제어한다. | ||
[[File: | [[File:기술백서 전체수정_70.jpg|none|thumb|400px|반도체 이종 구조의 계면에 형성된 이차원 전자층과 전극 패턴으로 형성된 이중 양자 우물 구조 모식도.<ref>https://https://www.quantuminfo.physik.rwth-aachen.de/cms/Quantuminfo/Forschung/Institut-fuer-Quantentechnologie/~dvux/Bluhm-GaAs/?lidx=1</ref> 참고문헌[10]의 그림을 재구성함.]] | ||
== 큐비트의 종류 == | == 큐비트의 종류 == | ||
| 67번째 줄: | 67번째 줄: | ||
<b>스핀 [[큐비트]] (spin Qubit)</b> | <b>스핀 [[큐비트]] (spin Qubit)</b> | ||
스핀 큐비트(Spin qubit)는 전자의 스핀을 [[큐비트]]로 이용한 것이다. 스핀 큐비트에 자기장을 가하면 스핀업과 다운이 축퇴(degenerate)되어 있지 않고 나누어진다. 따라서 spin-up | 스핀 큐비트(Spin qubit)는 전자의 스핀을 [[큐비트]]로 이용한 것이다. 스핀 큐비트에 자기장을 가하면 스핀업과 다운이 축퇴(degenerate)되어 있지 않고 나누어진다. 따라서 스핀 윗방향(spin-up)과 아랫방향(spin-down)을 이준위 시스템 큐비트로 사용한다. 스핀 큐비트를 조작할 때는 이준위 에너지 차이와 공명하는 마이크로파(microwave)를 사용하는데 이 방식을 전자 스핀 공명(electron spin resonance(ESR))이라고 한다. | ||
<b>전하 [[큐비트]] (charge Qubit)</b> | <b>전하 [[큐비트]] (charge Qubit)</b> | ||
전하 [[큐비트]]는 전자의 스핀이 아니라 전자가 양자점에 존재하는 여부를 바닥상태(ground state)와 들뜬상태(excited state)로 사용한다. 두개의 양자점( | 전하 [[큐비트]]는 전자의 스핀이 아니라 전자가 양자점에 존재하는 여부를 바닥상태(ground state)와 들뜬상태(excited state)로 사용한다. 두개의 양자점(double quantum dot(DQD))을 형성하여 사용되며 전자가 어느 양자점에 존재하는지를 확인하는 방식으로 구동한다. | ||
<b>하이브리드 [[큐비트]] (hybrid Qubit)</b> | <b>하이브리드 [[큐비트]] (hybrid Qubit)</b> | ||
스핀 큐비트의 장점인 긴 결맞음 시간(coherence time)과 전하 [[큐비트]]의 장점인 짧은 | 스핀 큐비트의 장점인 긴 결맞음 시간(coherence time)과 전하 [[큐비트]]의 장점인 짧은 제어 시간(manipulation time)을 이용하기 위해 두 스핀의 장점을 결합하여 만든 새로운 형태의 [[큐비트]]다. Si/SiGe 이종 구조(heterostructure) 내 형성된 두개의 양자점에서 세 개의 전자 스핀과 두개의 고유 상태(eigenstate)를 이용하여 구현되었다.<ref name=Kim> D. Kim et al., Quantum control and process tomography of a semiconductor quantum dot hybrid qubit, Nature <b>511</b>, 70(2014).https://doi.org/10.1038/nature13407.</ref> | ||
==반도체 양자점 구동 원리== | ==반도체 양자점 구동 원리== | ||
| 83번째 줄: | 83번째 줄: | ||
<b>초기화(initialization)</b> | <b>초기화(initialization)</b> | ||
이준위 스핀(spin) 상태의 초기화(initialization)는 단순한 방법으로는 양자점에 있는 스핀의 에너지가 바닥 상태(ground state)로 내려갈 때까지 오랜 시간 기다리는 방법으로 할 수 있다. 이 방법은 어떤 자기장에서든 할 수 있는 매우 간단한 초기화 방법이다. 이보다 빠른 초기화 방법으로는 |↑>를 아래에, |↓>를 위로 두고 사이에 페르미 에너지(Fermi energy)를 배치하는 것이다. 이때 |↑> 상태의 전자는 양자점에 머물러 있는 반면에 |↓> 상태의 전자는 저장고(reservoir)로 터널링되어 |↑> 방향으로 대체된다. 스핀 윗방향과 아랫방향의 터널링 시간(tunnel time)을 더한 것만큼의 시간을 기다리면 스핀은 높은 확률로 |↑>상태가 되어 초기화 시킬 수 있다.<ref name=initialization> R. Hanson et al., Electron spin qubits in quantum dots, in Proceedings of IEEE International Electron Devices Meeting 2004-IEDM Technical Digest,San Francisco, CA, USA(IEEE,San Francisco,2004) | 이준위 스핀(spin) 상태의 초기화(initialization)는 단순한 방법으로는 양자점에 있는 스핀의 에너지가 바닥 상태(ground state)로 내려갈 때까지 오랜 시간 기다리는 방법으로 할 수 있다. 이 방법은 어떤 자기장에서든 할 수 있는 매우 간단한 초기화 방법이다. 이보다 빠른 초기화 방법으로는 |↑>를 아래에, |↓>를 위로 두고 사이에 페르미 에너지(Fermi energy)를 배치하는 것이다. 이때 |↑> 상태의 전자는 양자점에 머물러 있는 반면에 |↓> 상태의 전자는 저장고(reservoir)로 터널링되어 |↑> 방향으로 대체된다. 스핀 윗방향과 아랫방향의 터널링 시간(tunnel time)을 더한 것만큼의 시간을 기다리면 스핀은 높은 확률로 |↑>상태가 되어 초기화 시킬 수 있다.<ref name=initialization> R. Hanson et al., Electron spin qubits in quantum dots, in Proceedings of IEEE International Electron Devices Meeting 2004-IEDM Technical Digest,San Francisco, CA, USA(IEEE,San Francisco,2004), 533. doi:10.1109/IEDM.2004.1419211</ref> 전하 큐비트의 경우, 왼쪽(L), 오른쪽(R) 게이트를 의 게이트 전위를 조절하여, 왼쪽 |L> 또는 오른쪽 |R> 양자점에만 전하가 존재하도록 초기화 하는 것이 가능하다. <ref name=Cao> G. Cao et al., Ultrafast universal quantum control of a quantum-dot charge qubit using Landau–Zener–Stu¨ckelberg interference, Nature Communications <b>4</b>, 1401 (2013).https://doi.org/10.1038/ncomms2412.</ref> | ||
<b>제어(manipulation)</b> | <b>제어(manipulation)</b> | ||
반도체 양자점은 왼쪽(L), 오른쪽(R) 게이트를 통해 이중 양자점을 형성하고 두 게이트 간 전위차이 ε∝V<sub>R</sub> - V<sub>L</sub>로 각 양자점의 전자의 상태를 제어할 수 있다. 또, 가운데 전위 장벽(T)의 전위 조절을 통해 양자점 간 터널링 정도를 제어하게 된다. 각 양자점 내 포획 전자의 전하량, 스핀 상태 등을 이용하여, 이준위 양자 상태를 형성하게 되는데, 게이트 간 전위차이 ε를 통해 각 양자 상태를 초기화하고 중첩 상태를 생성할 수 있다. 특히, ε=0 인 경우에는 터널링에 의해 연결되어 있는 두 양자 상태의 에너지가 같아져서 에너지 상태 간 반교차 (anticrossing)를 나타낸다. 이때 반교차 에너지 간격은 [[공통 기술#라비 진동 (Rabi Oscillation)|라비 진동 (Rabi Oscillation)]] 주파수와 비례한다. 양자 상태에 대한 결맞음 제어는 주로 이준위 상태와 공명하는 마이크로파 펄스를 통해 이뤄진다. | [[File:기술백서 전체수정_101edit.jpg|right|thumb|500px| (왼쪽) 금속전극들 사이에 형성된 전위장벽에 전자가 포획되고 반도체 내의 양자점이 생성된다. (오른쪽) 서로 연결되어 있는 양자상태의 에너지가 공명할 시 반교차 (anticrossing)에 따른 에너지 쪼개짐이 나타난다. <ref name=Cao> G. Cao et al., Ultrafast universal quantum control of a quantum-dot charge qubit using Landau–Zener–Stu¨ckelberg interference, Nature Communications <b>4</b>, 1401 (2013).</ref> 참고문헌[13]의 그림을 재구성함.]] | ||
제어 정확도는 결맞음 시간(coherence time)과 제어 시간(manipulation time)에 의해 결정된다. 결맞음 시간은 위상 어긋남 시간(dephasing time)이라고도 하며, 일반적으로 T<sub>2</sub>로 표기하고, 큐비트가 양자 성질을 얼마나 유지할 수 있는지를 나타낸다. 제어 시간은 회전각에 따라 π(T<sub>π</sub>)나 2π(T<sub>2π</sub>)로 표기하고, 단일 제어(single manipulation)에 대해 요구되는 시간을 나타낸다.<ref name=mani2>Zhang, X., Li, H. O., Cao, G., Xiao, M., Guo, G. C., & Guo, G. P. (2019). Semiconductor quantum computation. National Science Review, 6 | 반도체 양자점은 왼쪽(L), 오른쪽(R) 게이트를 통해 이중 양자점을 형성하고 두 게이트 간 전위차이 ε∝V<sub>R</sub> - V<sub>L</sub>로 각 양자점의 전자의 상태를 제어할 수 있다. 또, 가운데 전위 장벽(T)의 전위 조절을 통해 양자점 간 터널링 정도를 제어하게 된다. 각 양자점 내 포획 전자의 전하량, 스핀 상태 등을 이용하여, 이준위 양자 상태를 형성하게 되는데, 게이트 간 전위차이 ε를 통해 각 양자 상태를 초기화하고 중첩 상태를 생성할 수 있다. 특히, ε=0 인 경우에는 터널링에 의해 연결되어 있는 두 양자 상태의 에너지가 같아져서 에너지 상태 간 반교차(anticrossing)를 나타낸다. 이때 반교차 에너지 간격은 [[공통 기술#라비 진동 (Rabi Oscillation)|라비 진동 (Rabi Oscillation)]] 주파수와 비례한다. 양자 상태에 대한 결맞음 제어는 주로 이준위 상태와 공명하는 마이크로파 펄스를 통해 이뤄진다. | ||
제어 정확도는 결맞음 시간(coherence time)과 제어 시간(manipulation time)에 의해 결정된다. 결맞음 시간은 위상 어긋남 시간(dephasing time)이라고도 하며, 일반적으로 T<sub>2</sub>로 표기하고, 큐비트가 양자 성질을 얼마나 유지할 수 있는지를 나타낸다. 제어 시간은 회전각에 따라 π(T<sub>π</sub>)나 2π(T<sub>2π</sub>)로 표기하고, 단일 제어(single manipulation)에 대해 요구되는 시간을 나타낸다.<ref name=mani2>Zhang, X., Li, H. O., Cao, G., Xiao, M., Guo, G. C., & Guo, G. P. (2019). Semiconductor quantum computation. National Science Review, <b>6</b>, 32-54.https://doi.org/10.1093/nsr/nwy153.</ref> | |||
<b>측정(readout)</b> | <b>측정(readout)</b> | ||
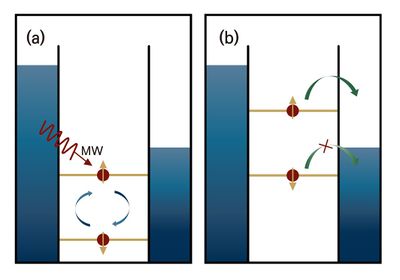
큐비트를 제어하는 중에는 스핀 윗방향과 아랫방향의 에너지 레벨은 드레인(drain)의 페르미 레벨 (Fermi level) 보다 밑에 위치한다. 측정(readout)을 하기 위해서는 스핀 윗방향과 아랫방향 상태 사이의 소스(source)와 드레인(drain)의 페르미 레벨을 조정한다. 그러면 스핀 윗방향의 전자는 양자점에 머물러있는 반면 스핀 아랫방향의 전자는 양자점을 통과하게 되는데 이를 이용하여 측정한다. 이 방법은 2004년에 Kouwenhoven과 Vandersypen의 연구팀이 고안해냈다.<ref name=Li> H. Li, B. Yao, T. Tu, and G. Guo, Quantum computation on gate-defined semiconductor quantum dots, Chinese Science Bulletin <b>57</b>, 1919 (2012).https://doi.org/10.1007/s11434-012-5091-5.</ref> | |||
[[File: | [[File:기술백서 전체수정_103edit.jpg|none|thumb|400px| 스핀에 따른 터널링(spin-selective tunneling)을 기반으로 하는 양자점 큐비트의 제어 및 측정 그림.<ref name=mani2> X. Zhang et al., Semiconductor quantum computation, National Science Review<b>6</b>, 32 (2019). doi:https://doi.org/10.1093/nsr/nwy153</ref> 참고문헌[8]의 그림을 재구성함.]] | ||
]] | |||
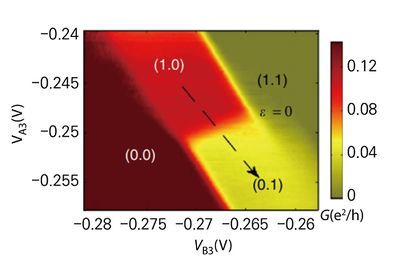
실험적으로 반도체 양자점의 전자 상태는 양자점 근처의 전하 센서, 양자 점 측정기(quantum point detector), 소스와 드레인 간 전류 등을 통해 확인하게 되며, | 실험적으로 반도체 양자점의 전자 상태는 양자점 근처의 전하 센서, 양자 점 측정기(quantum point detector), 소스와 드레인 간 전류 등을 통해 확인하게 되며, 아래 그림은 이러한 소자 내 검출 신호를 통해 확인 할 수 있는 게이트 간 전위 차에 따른 양자 상태에 대한 도표 예시이다. | ||
[[File: | [[File:기술백서 전체수정_99edit.jpg|none|thumb|400px| GaAs/AlGaAs 이중 양자점(double quantum dot)의 게이트 전위에 따른 왼쪽, 오른쪽 양자점 전하 큐비트 측정 신호 도표. <ref name=Cao>G. Cao et al., Ultrafast universal quantum control of a quantum-dot charge qubit using Landau–Zener–Stu¨ckelberg interference, Nature Communications <b>4</b>, 1401.https://doi.org/10.1038/ncomms2412. (2013).</ref> 참고문헌[13]의 그림을 재구성함.]] | ||
== 개발 현황 == | == 개발 현황 == | ||
[[File: | [[File:기술백서 전체수정_96edit.jpg|none|thumb|300px|큐비트의 읽기/쓰기 나노 구조<ref name=Jarryd J. Pla>Jarryd J. Pla et al.,High-fidelity readout and control of a nuclear spin qubit in silicon <b>496</b>, 334 (2013).https://doi.org/10.1038/nature12011.</ref> 참고문헌[15]의 그림을 재구성함.]] | ||
[[반도체 기반#양자점 (Quantum Dot; 퀀텀닷)| | [[반도체 기반#양자점 (Quantum Dot; 퀀텀닷)|양자점]] [[큐비트]]는 반도체 내부에 게이트 전압을 이용하거나 도핑을 통해 가상의 원자를 만드는 큐비트이다. 대표적으로는 2018년 보고된 GaAs/AlGaAs 이종 접합에 게이트 전압을 통해 전자의 이동을 제한하는 방식으로 만들어진 단일 전자 큐비트가 있다.<ref name=Camenzind>L. C. Camenzind et al., Hyperfine-phonon spin relaxation in a single-electron GaAs quantum dot, Nature communications <b>9</b>, 1 (2018).https://doi.org/10.1038/s41467-018-05879-x.</ref> 이 큐비트는 [[반도체 기반#양자점 (Quantum Dot; 퀀텀닷)|양자점]] 내부 전자의 스핀을 이용하였으며 약 57초의 [[결맞음]] 시간을 보였다. 또한 도핑을 이용한 큐비트로는 실리콘 내에 인(P)원자를 도핑해 인의 핵 스핀을 이용하는 큐비트가 있다. 핵 스핀을 이용하는 경우 저온에서 2시간 이상 붕괴(decay)가 거의 보이지 않았으며 상온에서도 [[결맞음]] 시간이 2시간이 넘어갔다고 보고되었다. <ref name=Saeedi>K. Saeedi et al., Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science <b>342</b>, 830 (2013). doi:10.1126/science.1239584 </ref> | ||
2021년 11월 23일 (화) 18:01 기준 최신판
<양자 기술백서 |
결정 내 색중심 (color center)[편집]
색중심의 종류[편집]
결정에 존재하는 단일 불순물(impurity), 공동 (vacancy) 등과 같은 점 결함(point defect)은 고체 내 속박된 인공 원자로서, 스핀 및 광학 큐비트를 고체 시스템에서 생성하는 중요한 역할을 한다. 대표적인 점결함 예인 Nitrogen-Vacancy (NV) 색중심은 다이아몬드의 결정격자에서 탄소원자가 제거되어 생성된 공극에 질소원자가 결합하고 인접한 격자에서 하나의 탄소가 빠져 비어있는 상태인 점결함이다. NV 색중심은 중성(NV0)또는 음성(NV-)을 띌 수 있다. 음성을 띌 때 총 두 개의 홀전자(탄소와 공극에서 각각 하나씩)를 가지며 바닥상태(ground state)에서 스핀 삼중항 상태(triplet state)(S=1)인 스핀 큐비트가 된다. 이러한 결정 내 색중심은 다이아몬드 내에서도 Silicon vacancy (SiV), Germanium vacancy (GeV) 등 다양한 형태로 존재할 수 있고, 다이아몬드 외에도 SiC, GaN, h-BN 등과 같은 다양한 결정에서 연구되고 있다.
NV 색중심의 에너지 준위와 스핀 구조[편집]
NV 색중심의 에너지 준위는 다이아몬드의 넓은 전도띠(conduction band)와 원자가띠(valence band) 간격 내 깊은 곳에 위치해있다. 아래 그림은 NV 색중심의 삼중항 상태(triplet state)를 갖는 전자 스핀 (S=1)의 에너지 준위를 나타내고 있다. 외부 자기장이 없는 환경에서 ms=±1 인 상태와 ms=0 인 상태는 2.87 GHz 의 무자기장 쪼개짐(zero-field splitting)을 갖는다. NV 색중심의 전자 스핀은 삼중항 상태(3A2, 3E)와 함께 단일항 상태(singlet state)(1A1, 1E)에도 존재할 수 있고, 삼중항 상태에서 단일항 상태로의 전이(transition) 또한 가능하다.
NV 색중심의 전자 스핀 큐비트 구동원리[편집]
NV 색중심 전자 스핀은 에너지 준위를 기반, 레이저 광펌핑, 마이크로파, 발광을 이용하여 스핀 큐비트의 초기화, 제어, 측정이 가능하다. 실질적으로는 바닥 삼중항 상태의 전자 스핀을 이준위 큐비트 시스템으로 사용하게 되는데 ms=0 스핀 상태를 큐비트의 |0> 으로 ms=±1 스핀 상태 중 하나를 큐비트의 |1> 로 사용가능하다. 축퇴(degeneracy)되어 있는 ms=±1 스핀상태는 외부자기장을 인가하는 경우 축퇴상태가 쪼깨지게 되어 각 스핀 상태를 선택적으로 접근할 수 있다.
초기화(initialization)
바닥 삼중항 상태(3A2)의 전자는 가시광 파장 (532 nm)의 레이저를 가하는 경우 스핀이 보존되는 들뜬 삼중항 상태(3E)로 여기된다. 이때 3E의 ms=0 상태의 전자는 원래의 3A2의 ms=0 상태로 떨어지며 가시광 빛(637 nm)을 방출한다. 반면 3E의 ms=±1로 여기된 전자는 3A2의 ms=±1상태로 직접 떨어지거나 30% 정도의 확률로 단일항 상태(singlet state)인 1A를 거쳐 3A2의 ms=0로 떨어지게 된다. 따라서, 전자를 여기시키는 과정을 반복하면 결국 모든 전자들이 3A2의 ms=0에 있게되어, 전자 스핀 큐비트를 |0>으로 초기화 시킬 수 있다.
제어(manipulation)
ms=0로 초기화된 스핀은 2.87 GHz 정도 크기의 마이크로파를 이용하여 ms=±1 여기시킬 수 있다. 이때, 쪼개짐 간격과 정확히 일치하는(resonant) 마이크로파 (rotation pulse)를 인가하게 되면 스핀 상태가 마이크파의 인가 펄스 폭에 대한 라비 진동 (Rabi oscillation)을 하게 되고 이를 통해 이준위 전자 스핀에 대한 결맞음 제어가 가능하다.
측정(readout)
NV 색중심 전자 스핀 상태의 측정은 공초점 현미경 기반의 광측정자기공명 (optically detected magnetic resonance,(ODMR)) 실험을 통해 이뤄진다. 스핀 초기화 과정과 마찬가지로 가시광 레이저를 이용하여 전자를 여기시키게 되면, 3A2의 ms=0 스핀 상태의 경우, 삼중항 상태(triplet state) (3E의 ms=0) 사이에서만 직접 여기와 직접 천이 과정을 거치게 되지만, ms=±1 스핀 상태의 경우, 단일항 상태(singlet state)로의 부분천이가 발생하여, 직접 천이 파장에 해당하는 637 nm 근처의 광신호 세기를 비교 시, 스핀 상태에 따라 발광 세기에 차이가 발생된다. 이를 통해 전자 스핀이 어떠한 상태에 있는지 정보를 얻게 된다.
다이아몬드의 스핀 큐비트를 이용한 양자 게이트 구현과 광자를 이용한 네트워크 형성[편집]
다이아몬드의 1.1%는 스핀 1/2 시스템인 13C로 이루어지고 나머지는 모두 스핀이 없는 12C로 이루어진다. 따라서 NV 색중심 근처에 13C 원자가 존재하게 되면, 전자 스핀과 핵 스핀 간 서로 상호작용을 하게된다. 우선 전자 스핀 주위에 존재하는 핵 스핀은 전자스핀에 영향을 주기 때문에 결어긋남(decoherence)을 일으키는 주원인으로 작용한다. 이러한 전자 스핀에 형향을 주는 주위환경과의 DC/AC 노이즈를 제거하기 위하여 RF 펄스를 이용한 스핀 메아리 (spin echo)와 동적 디커플링 (dynamical decoupling) 방법 등을 사용할 수 있고, 다이아몬드 내 13C 원자 생성이 억제된 성장기술 등을 이용 전자 스핀의 결맞음 시간을 늘려주기도 한다.[3]
반면, 탄소의 핵 스핀도 하나의 큐비트로 사용할 수 있어, 핵스핀과 전자 스핀간의 상호작용을 잘 활용하게 되면 전자 스핀을 이용하여 인접 핵 스핀의 상태를 제어하는 것이 가능하여 양자 게이트(quantum gate) 구현이 가능해진다. 전자 스핀 하나와 핵 스핀 하나를 기반으로 한 controlled-NOT (CNOT)를 이용하게 되면 NV 색중심 주변의 탄소 핵 스핀을 컨트롤할 수 있고, 이를 이용하여, 전자 스핀 정보를 핵스핀에 긴 시간동안 저장하는 것 또한 가능하다.[4]
다수 스핀 큐비트 간 원거리 양자 얽힘을 구현하는 방법으로는 NV 색중심의 에너지 준위간 천이에 의해 방출되는 광자를 이용하는 방법이다. 색중심의 스핀 정보는 방출 광자의 편광 등에 저장이 되는데, 서로 떨어져 있는 스핀 큐비트에서 방출 된 광자 간 양자 간섭 등을 수행하게 되면, 원거리 스핀 큐비트 간 양자 얽힘(quantum entanglement) 구현이 가능하여 양자 네트워크 로써 확장이 가능하다.[5]
개발 현황[편집]
결정 내 색중심을 이용한 큐비트로는 다이아몬드 내에 NV 색중심을 이용한 큐비트가 대표적이다. 2018년 NV중심으로 결맞음 시간(T1)이 1시간에 달하는 큐비트가 만들어졌다.[6]
NV 색중심의 전자 스핀 하나와 주위 핵스핀 9개가 서로 연결되어 얽힘상태 구현이 가능한 10 큐비트 레지스터가 구현되어 확장성에 대한 가능성을 보여주기도 하였다. [7]
게이트 양자점 (gate quantum dot)[편집]
반도체 양자점 생성 원리[편집]
반도체 양자점은 인공 원자(artificial atom) 라고도 하며 반도체 내에서 양자점을 형성하는 게이트를 제작하여 개별 전자를 포획한뒤 게이트 전위 차 등을 이용하여 전기적으로 포획 전자의 양자 상태를 결맞음 제어할 수 있다. 양자점에 전자가 갇히면 포획 전자들의 교환(exchange) 상호작용, 전하 (charge), 스핀 (spin) 등을 큐비트로 이용할 수 있다.[8] 가장 많이 사용되는 소재는 GaAs/AlGaAs, Si/SiGe 와 같은 이종구조(heterostructure)이다. 특히, GaAs/AlGaAs 이종구조는 전자이동도가 높은 특성을 가지고 있어 제일 먼저 양자점 기반의 큐비트를 만드는데 사용되었다.[9] 반도체 이종 구조의 접합 계면에서는 이차원 전자 가스(two-dimensional electron gas (2DEG))가 생성된다. 형성된 이차원 전자 가스층은 전자를 수직방향으로 구속하는 효과와 함께 전자를 공급하는 저장고(reservoir) 역할을 한다. 추가적으로 반도체 웨이퍼에 게이트(gate) 역할을 하는 금속 패턴을 형성 후, 음의 전위를 갖는 양자우물에 전자를 수평 방향으로 포획한다. 이로써, 3차원으로 포획된 반도체 양자점이 생성이 가능하다. 각 게이트의 전위를 조절하여 양자점 내 전자를 이동하거나 양자 상태를 제어한다.
큐비트의 종류[편집]
스핀 큐비트 (spin Qubit)
스핀 큐비트(Spin qubit)는 전자의 스핀을 큐비트로 이용한 것이다. 스핀 큐비트에 자기장을 가하면 스핀업과 다운이 축퇴(degenerate)되어 있지 않고 나누어진다. 따라서 스핀 윗방향(spin-up)과 아랫방향(spin-down)을 이준위 시스템 큐비트로 사용한다. 스핀 큐비트를 조작할 때는 이준위 에너지 차이와 공명하는 마이크로파(microwave)를 사용하는데 이 방식을 전자 스핀 공명(electron spin resonance(ESR))이라고 한다.
전하 큐비트 (charge Qubit)
전하 큐비트는 전자의 스핀이 아니라 전자가 양자점에 존재하는 여부를 바닥상태(ground state)와 들뜬상태(excited state)로 사용한다. 두개의 양자점(double quantum dot(DQD))을 형성하여 사용되며 전자가 어느 양자점에 존재하는지를 확인하는 방식으로 구동한다.
하이브리드 큐비트 (hybrid Qubit)
스핀 큐비트의 장점인 긴 결맞음 시간(coherence time)과 전하 큐비트의 장점인 짧은 제어 시간(manipulation time)을 이용하기 위해 두 스핀의 장점을 결합하여 만든 새로운 형태의 큐비트다. Si/SiGe 이종 구조(heterostructure) 내 형성된 두개의 양자점에서 세 개의 전자 스핀과 두개의 고유 상태(eigenstate)를 이용하여 구현되었다.[11]
반도체 양자점 구동 원리[편집]
초기화(initialization)
이준위 스핀(spin) 상태의 초기화(initialization)는 단순한 방법으로는 양자점에 있는 스핀의 에너지가 바닥 상태(ground state)로 내려갈 때까지 오랜 시간 기다리는 방법으로 할 수 있다. 이 방법은 어떤 자기장에서든 할 수 있는 매우 간단한 초기화 방법이다. 이보다 빠른 초기화 방법으로는 |↑>를 아래에, |↓>를 위로 두고 사이에 페르미 에너지(Fermi energy)를 배치하는 것이다. 이때 |↑> 상태의 전자는 양자점에 머물러 있는 반면에 |↓> 상태의 전자는 저장고(reservoir)로 터널링되어 |↑> 방향으로 대체된다. 스핀 윗방향과 아랫방향의 터널링 시간(tunnel time)을 더한 것만큼의 시간을 기다리면 스핀은 높은 확률로 |↑>상태가 되어 초기화 시킬 수 있다.[12] 전하 큐비트의 경우, 왼쪽(L), 오른쪽(R) 게이트를 의 게이트 전위를 조절하여, 왼쪽 |L> 또는 오른쪽 |R> 양자점에만 전하가 존재하도록 초기화 하는 것이 가능하다. [13]
제어(manipulation)
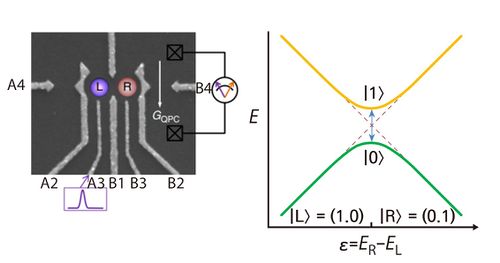
반도체 양자점은 왼쪽(L), 오른쪽(R) 게이트를 통해 이중 양자점을 형성하고 두 게이트 간 전위차이 ε∝VR - VL로 각 양자점의 전자의 상태를 제어할 수 있다. 또, 가운데 전위 장벽(T)의 전위 조절을 통해 양자점 간 터널링 정도를 제어하게 된다. 각 양자점 내 포획 전자의 전하량, 스핀 상태 등을 이용하여, 이준위 양자 상태를 형성하게 되는데, 게이트 간 전위차이 ε를 통해 각 양자 상태를 초기화하고 중첩 상태를 생성할 수 있다. 특히, ε=0 인 경우에는 터널링에 의해 연결되어 있는 두 양자 상태의 에너지가 같아져서 에너지 상태 간 반교차(anticrossing)를 나타낸다. 이때 반교차 에너지 간격은 라비 진동 (Rabi Oscillation) 주파수와 비례한다. 양자 상태에 대한 결맞음 제어는 주로 이준위 상태와 공명하는 마이크로파 펄스를 통해 이뤄진다. 제어 정확도는 결맞음 시간(coherence time)과 제어 시간(manipulation time)에 의해 결정된다. 결맞음 시간은 위상 어긋남 시간(dephasing time)이라고도 하며, 일반적으로 T2로 표기하고, 큐비트가 양자 성질을 얼마나 유지할 수 있는지를 나타낸다. 제어 시간은 회전각에 따라 π(Tπ)나 2π(T2π)로 표기하고, 단일 제어(single manipulation)에 대해 요구되는 시간을 나타낸다.[8]
측정(readout)
큐비트를 제어하는 중에는 스핀 윗방향과 아랫방향의 에너지 레벨은 드레인(drain)의 페르미 레벨 (Fermi level) 보다 밑에 위치한다. 측정(readout)을 하기 위해서는 스핀 윗방향과 아랫방향 상태 사이의 소스(source)와 드레인(drain)의 페르미 레벨을 조정한다. 그러면 스핀 윗방향의 전자는 양자점에 머물러있는 반면 스핀 아랫방향의 전자는 양자점을 통과하게 되는데 이를 이용하여 측정한다. 이 방법은 2004년에 Kouwenhoven과 Vandersypen의 연구팀이 고안해냈다.[14]
실험적으로 반도체 양자점의 전자 상태는 양자점 근처의 전하 센서, 양자 점 측정기(quantum point detector), 소스와 드레인 간 전류 등을 통해 확인하게 되며, 아래 그림은 이러한 소자 내 검출 신호를 통해 확인 할 수 있는 게이트 간 전위 차에 따른 양자 상태에 대한 도표 예시이다.
개발 현황[편집]
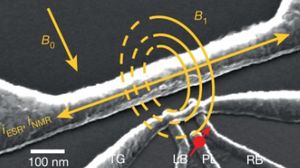
<ref> 태그가 잘못되었습니다;
잘못된 이름입니다, 예: 너무 많습니다 참고문헌[15]의 그림을 재구성함.양자점 큐비트는 반도체 내부에 게이트 전압을 이용하거나 도핑을 통해 가상의 원자를 만드는 큐비트이다. 대표적으로는 2018년 보고된 GaAs/AlGaAs 이종 접합에 게이트 전압을 통해 전자의 이동을 제한하는 방식으로 만들어진 단일 전자 큐비트가 있다.[15] 이 큐비트는 양자점 내부 전자의 스핀을 이용하였으며 약 57초의 결맞음 시간을 보였다. 또한 도핑을 이용한 큐비트로는 실리콘 내에 인(P)원자를 도핑해 인의 핵 스핀을 이용하는 큐비트가 있다. 핵 스핀을 이용하는 경우 저온에서 2시간 이상 붕괴(decay)가 거의 보이지 않았으며 상온에서도 결맞음 시간이 2시간이 넘어갔다고 보고되었다. [16]
참고 문헌[편집]
- ↑ A. Haque and S. Sumaiya, An overview on the formation and processing of nitrogen-vacancy photonic centers in diamond by ion implantation, Journal of Manufacturing and Materials Processing 1, 1 (2017).doi:https://doi.org/10.3390/jmmp1010006
- ↑ M. Lee, J. Yoon, and D. Lee,Magnetometers-Fundamentals and Applications of Magnetism(intechOpen, 2019)doi:https://dx.doi.org/10.5772/intechopen.75335.
- ↑ G. Balasubramanian et al., Ultralong spin coherence time in isotopically engineered diamond, Nature materials 8, 383 (2009).https://doi.org/10.1038/nmat2420.
- ↑ L.Childress et al.,Coherent dynamics of coupled electron and nuclear spin qubits in diamond, Science 314, 281 (2006).doi:10.1126/science.1131871.
- ↑ H. Bernien et al., Heralded entanglement between solid-state qubits separated by three metres, Nature 497, 86 (2013).https://doi.org/10.1038/nature12016.
- ↑ 이동: 6.0 6.1 M. H. Abobeih et al., One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment, Nature Communications 9, 2552 (2018).https://doi.org/10.1038/s41467-018-04916-z. 인용 오류: 잘못된
<ref>태그; "Abobeih"이 다른 콘텐츠로 여러 번 정의되었습니다 - ↑ C. E Bradley et al., A ten-qubit solid-state spin register with quantum memory up to one minute, Physical Review X 9, 031045 (2019).https://doi.org/10.1103/PhysRevX.9.031045.
- ↑ 이동: 8.0 8.1 8.2 X. Zhang et al., Semiconductor quantum computation. National Science Review, 6, 32-54 (2019).https://doi.org/10.1093/nsr/nwy153. 인용 오류: 잘못된
<ref>태그; "mani2"이 다른 콘텐츠로 여러 번 정의되었습니다 인용 오류: 잘못된<ref>태그; "mani2"이 다른 콘텐츠로 여러 번 정의되었습니다 - ↑ X. Zhang et al., Qubits based on semiconductor quantum dots, Chinese Physics B, 27 020305 (2018). doi:10.1088/1674-1056/27/2/020305/meta.
- ↑ https://https://www.quantuminfo.physik.rwth-aachen.de/cms/Quantuminfo/Forschung/Institut-fuer-Quantentechnologie/~dvux/Bluhm-GaAs/?lidx=1
- ↑ D. Kim et al., Quantum control and process tomography of a semiconductor quantum dot hybrid qubit, Nature 511, 70(2014).https://doi.org/10.1038/nature13407.
- ↑ R. Hanson et al., Electron spin qubits in quantum dots, in Proceedings of IEEE International Electron Devices Meeting 2004-IEDM Technical Digest,San Francisco, CA, USA(IEEE,San Francisco,2004), 533. doi:10.1109/IEDM.2004.1419211
- ↑ 이동: 13.0 13.1 13.2 G. Cao et al., Ultrafast universal quantum control of a quantum-dot charge qubit using Landau–Zener–Stu¨ckelberg interference, Nature Communications 4, 1401 (2013).https://doi.org/10.1038/ncomms2412. 인용 오류: 잘못된
<ref>태그; "Cao"이 다른 콘텐츠로 여러 번 정의되었습니다 인용 오류: 잘못된<ref>태그; "Cao"이 다른 콘텐츠로 여러 번 정의되었습니다 - ↑ H. Li, B. Yao, T. Tu, and G. Guo, Quantum computation on gate-defined semiconductor quantum dots, Chinese Science Bulletin 57, 1919 (2012).https://doi.org/10.1007/s11434-012-5091-5.
- ↑ L. C. Camenzind et al., Hyperfine-phonon spin relaxation in a single-electron GaAs quantum dot, Nature communications 9, 1 (2018).https://doi.org/10.1038/s41467-018-05879-x.
- ↑ K. Saeedi et al., Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830 (2013). doi:10.1126/science.1239584