광자 기반: 두 판 사이의 차이
(→참고 문헌) |
편집 요약 없음 |
||
| (사용자 5명의 중간 판 77개는 보이지 않습니다) | |||
| 10번째 줄: | 10번째 줄: | ||
= 개요 = | = 개요 = | ||
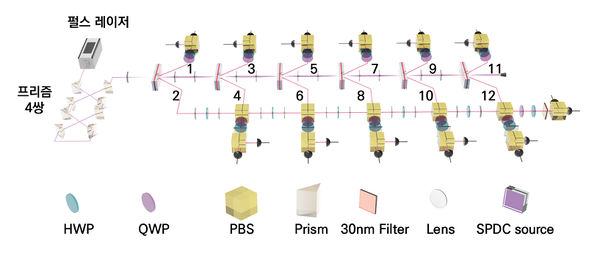
[[File: | [[File:기술백서 전체수정 6차 65 편집.jpg|none|thumb|600px|그림 1. 12 큐비트 얽힘 상태 생성의 모식도.<ref name= "Zhong2018"> H. S. Zhong, Y. Li, W. Li,L. C. Peng,Z. E. Su, Y. Hu, L. Zhang, 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion, Physical Review Letters '''121''', 250505 (2018). doi:10.1103/PhysRevLett.121.250505.</ref> 펄스 레이저가 총 6개의 비선형 결정을 통과하며 자발 매개변수하향변화 SPDC(Spontaneous Parametric Down Conversion)에 의해 얽힘 상태인 12개의 광자로 나누어진다. | ||
]] | ]] | ||
양자컴퓨팅에서 광자는 [[큐비트]]의 주요 구현 방식 중 하나로 연구되고 있으며, 뚜렷한 장점, 즉 특별히 상호작용하는 물질과 접촉하지 않는 이상 환경과 상호작용을 잘 하지 않아 [[결맞음]]이 오래 유지된다는 특성이 있다. 또한 이러한 결맞음 특성과 함께 빛의 속도로 빠르게 이동한다는 특성상 멀리 보내기도 수월하다는 장점을 가지고 있다. 이러한 점 때문에 광자는 양자컴퓨팅뿐 아니라 [[양자통신]]에서 활발하게 연구되고 있는 주제이기도 하다. 또한 광자 큐비트는 기존의 벌크, 광섬유 기반의 광학 기구를 이용하여 양자 상태를 제어하기에 다른 플랫폼에 비해 시스템 구축이 용이하다는 장점도 가지고 있다. | 양자컴퓨팅에서 광자는 [[큐비트]]의 주요 구현 방식 중 하나로 연구되고 있으며, 뚜렷한 장점, 즉 특별히 상호작용하는 물질과 접촉하지 않는 이상 환경과 상호작용을 잘 하지 않아 [[결맞음]]이 오래 유지된다는 특성이 있다. 또한 이러한 결맞음 특성과 함께 빛의 속도로 빠르게 이동한다는 특성상 멀리 보내기도 수월하다는 장점을 가지고 있다. 이러한 점 때문에 광자는 양자컴퓨팅뿐 아니라 [[양자통신]]에서 활발하게 연구되고 있는 주제이기도 하다. 또한 광자 큐비트는 기존의 벌크, 광섬유 기반의 광학 기구를 이용하여 양자 상태를 제어하기에 다른 플랫폼에 비해 시스템 구축이 용이하다는 장점도 가지고 있다. | ||
반면에 이러한 특성은 광자 기반 양자컴퓨터의 약점으로 꼽히기도 한다. 광자 간 상호작용은 물론이고 다른 물질을 이용하여 광자의 주파수를 변환하는 비선형 변환의 경우 상호작용 정도가 매우 약하기 때문에 결정론적인 [[게이트]]를 만들기 어렵고 확률적인 게이트를 사용할 수밖에 없는 경우가 많다. 또한 이러한 약한 상호작용의 특성과 맞물려 대량의 광자를 [[얽힘 상태]]로 만드는 것이 어렵다는 점도 하나의 특징으로 꼽히고 있다. 현재까지 얽힘 상태로 가장 많은 수의 광자를 생성한 것으로 12 광자 얽힘 상태가 알려져 있다 ( | 반면에 이러한 특성은 광자 기반 양자컴퓨터의 약점으로 꼽히기도 한다. 광자 간 상호작용은 물론이고 다른 물질을 이용하여 광자의 주파수를 변환하는 비선형 변환의 경우 상호작용 정도가 매우 약하기 때문에 결정론적인 [[게이트]]를 만들기 어렵고 확률적인 게이트를 사용할 수밖에 없는 경우가 많다. 또한 이러한 약한 상호작용의 특성과 맞물려 대량의 광자를 [[얽힘 상태]]로 만드는 것이 어렵다는 점도 하나의 특징으로 꼽히고 있다. 현재까지 얽힘 상태로 가장 많은 수의 광자를 생성한 것으로 12 광자 얽힘 상태가 알려져 있다 (그림 1 참고).<ref name= "Zhong2018"/> | ||
= 양자 광학 = | = 양자 광학 = | ||
| 21번째 줄: | 21번째 줄: | ||
== 큐비트== | == 큐비트== | ||
광자란 일반적인 의미로, 빛으로서 최소 단위 에너지를 갖는 알갱이이다. 광자 기반 양자컴퓨팅에 사용되는 큐비트로는, 광자의 다양한 자유도를 이용한 여러가지 종류가 있다. 우선 선편광 중 한 축의 편광과 그에 수직한 다른 편광을 사용하는 방법이 있다. 선편광된 광자는 편광판이나 | 광자란 일반적인 의미로, 빛으로서 최소 단위 에너지를 갖는 알갱이이다. 광자 기반 양자컴퓨팅에 사용되는 큐비트로는, 광자의 다양한 자유도를 이용한 여러가지 종류가 있다. 우선 선편광 중 한 축의 편광과 그에 수직한 다른 편광을 사용하는 방법이 있다. 선편광된 광자는 편광판이나 편광 빔분할기를 이용해 쉽게 만들 수 있고, 반파장판을 이용해 편광의 각도를 회전시킬 수 있으며, 다시 편광판과 측정기의 조합을 이용해 특정 편광을 측정할 수 있는 등, 큐비트 조작이 용이하기 때문에 광자 기반 양자컴퓨팅 및 기타 광자 관련 실험에 널리 쓰인다. 편광 방향은 일반적으로 광평면에 수평한 수평 방향 편광 $$\left| H \right\rangle$$ 와 그에 수직한 수직방향 편광 $$\left| V \right\rangle$$ 를 많이 사용한다. 이 경우 광자 큐비트 상태 $$\left| \psi \right\rangle$$ 는, | ||
\[\left| \psi \right\rangle= \alpha\left| H \right\rangle + \beta\left| V \right\rangle\] | \[\left| \psi \right\rangle= \alpha\left| H \right\rangle + \beta\left| V \right\rangle\] | ||
로 표현할 수 있다 (여기서 $$\alpha, \beta$$ 는 $$|\alpha|^{2} + |\beta|^{2}= 1$$ 인 복소수). 그 밖에 서로 다른 두 주파수를 큐비트의 두 상태로 정하고 이 두 주파수와 반응하는 원자나 결정을 사용하여 큐비트 조작을 하는 방법, 두 개의 공진기나 경로를 만들어놓고 광자가 둘 중 어느 쪽에 있는지를 큐비트의 상태로 이용하는 방법, 궤도 각운동량을 큐비트로써 이용하는 방법 등이 있다. | 로 표현할 수 있다 (여기서 $$\alpha, \beta$$ 는 $$|\alpha|^{2} + |\beta|^{2}= 1$$ 인 복소수). 그 밖에 서로 다른 두 주파수를 큐비트의 두 상태로 정하고 이 두 주파수와 반응하는 원자나 결정을 사용하여 큐비트 조작을 하는 방법, 두 개의 공진기나 경로를 만들어놓고 광자가 둘 중 어느 쪽에 있는지를 큐비트의 상태로 이용하는 방법, 궤도 각운동량을 큐비트로써 이용하는 방법 등이 있다. | ||
== 결맞음 상태 (Coherent State)== | == 결맞음 상태 (Coherent State)== | ||
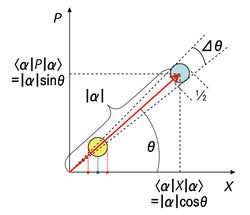
[[File: | [[File:기술백서 전체수정_66._편집.jpg|right|thumb|250px|그림 2. 위상공간에서의 결맞음 상태 $$\left| \alpha \right\rangle$$를 나타낸 그림. X와 P는 쿼드러처이며, $$|\alpha|$$는 진폭, $$\theta$$는 위상이다.<ref>https://en.wikipedia.org/wiki/Coherent_states</ref> | ||
]] | ]] | ||
결맞음 상태란, 소멸 연산자[[(annihilation operator)]] $$\widehat{a}$$ 의 고유 상태, 즉 | |||
\[\widehat{a}\left| \alpha \right\rangle= \alpha\left| \alpha \right\rangle\] | \[\widehat{a}\left| \alpha \right\rangle= \alpha\left| \alpha \right\rangle\] | ||
의 $$\left| \alpha \right\rangle$$ 으로 정의된다. 이 때 $$\alpha= |\alpha|e^{\text{iθ}}$$ 로 나타냈을 때 $$|\alpha|$$는 진폭, $$\theta$$는 위상이라고 부른다. 이는 고전역학에서의 조화 진동자에 있는 입자의 상태를 | 의 $$\left| \alpha \right\rangle$$ 으로 정의된다. 이 때 $$\alpha= |\alpha|e^{\text{iθ}}$$ 로 나타냈을 때 $$|\alpha|$$는 진폭, $$\theta$$는 위상이라고 부른다. 이는 고전역학에서의 조화 진동자에 있는 입자의 상태를 [[양자역학]]적으로 해석할 때 사용하기 위해 고안된 상태로, 위상공간에서는 그림 2와 같이 나타낼 수 있다. X와 P는 위상공간의 축을 만드는 쿼드러처이며, 진폭과 위상은 각각 불확정성을 갖고 있다.<ref name =Olivares> S. Olivares, Quantum optics in the phase space, The European Physical Journal Special Topics '''203''' (2012). doi:10.1140/epjst/e2012-01532-4.</ref> 결맞음 상태의 중요한 특징 중 하나는, 이 상태가 최소 불확정성 상태, 즉 $$\Delta X= \Delta P =1/2$$ 라는 점이다. 여기서 $$\text{ΔX}$$, $$\text{ΔP}$$ 또는 임의의 쿼드러처로의 불확정성을 줄이는 대신 다른 쿼드러처의 불확정성을 높인 조임 상태를 만들 수도 있다. | ||
== 조임 상태 (Squeezed State) == | == 조임 상태 (Squeezed State) == | ||
결맞음 상태에서 하나의 쿼드러처로 불확정성을 줄인 상태를 조임상태라고 한다. 이 때 $$\Delta X\Delta P > 1/4$$ 가 되며, 양자광학에서는 일반적으로 두 광자의 조임 정도가 이 둘의 [[양자 얽힘]] 정도와 관련이 있기 때문에 중요하게 다루어진다.<ref name=Marek>P. Marek, M. Paternostro, & M. S. Kim, Characterization of the entanglement of two squeezed states, Physical Review A '''74''', 032311 (2006)</ref> | |||
= 광학 기구 = | = 광학 기구 = | ||
== | == 빔분할기 (Beam Splitter)== | ||
빔분할기는 고전광학적으로는 빔을 일정 비율의 출력으로 나눠서 서로 다른 경로로 보내주는 장치이다. 그러나 양자광학적으로는, 단일광자에 대해 출력을 나누는 것은 불가능하기 때문에 확률적으로 경로가 선택되게 된다. 입력 모드 $${\widehat{a}}_{0}$$, $${\widehat{a}}_{1}$$ 과 출력 모드 $${\widehat{a}}_{2}$$, $${\widehat{a}}_{3}$$ 에 대해 다음과 같이 변환 관계로 나타낼 수 있으며, 이에 따라 확률진폭이 나눠지게 된다. | |||
\[\begin{pmatrix} | \[\begin{pmatrix} | ||
| 63번째 줄: | 61번째 줄: | ||
\end{pmatrix}\] | \end{pmatrix}\] | ||
50:50 빔분할기의 경우 반사빔과 투과빔이 $$e^{\pm i\frac{\pi}{2}}=\pm i= cos(\frac{\pi}{2})\pm isin(\frac{\pi}{2})$$의 위상차가 발생한다. 투과빔이 $${+\frac{\pi}{2}}$$의 위상차를 가진다고 가정했을 때, 입력모드와 출력모드의 관계는 다음과 같다. | |||
== | \[{\widehat{a}}_{2}= \frac{1}{\sqrt{2}}\left({\widehat{a}}_{0} + i{\widehat{a}}_{1} \right), {\widehat{a}}_{3} =\frac{1}{\sqrt{2}}\left( i{\widehat{a}}_{0} + {\widehat{a}}_{1} \right)\] | ||
== 위상 변조기 (Phase Shifter) == | |||
광자의 진행을 늦춤으로서 위상을 변화시키는 장치이다. 빛의 속도를 느리게 하는 물질을 이용하거나, 단순히 액츄에이터 등을 사용해서 경로의 길이를 변화시킴으로써 위상 변화를 만들어줄 수 있다. 양자컴퓨팅에서는, [[큐비트]]를 이루는 두 모드 간의 위상 변화는 곧 [[큐비트]]의 국소 위상을 변화시키는 것이기 때문에, 광자 큐비트의 제어에서 필수 부품이라고 할 수 있다. | |||
[[File: | == 비선형 매질 (Nonlinear Medium) == | ||
[[File:기술백서 전체수정_67_편집.jpg|none|thumb|400px|그림 3. 자발매개하향변환의 모식도. pump를 통해 비선형 매질로 입사한 광자는 signal과 idler라고 불리는 두 출력으로 각각 하나의 광자씩 나뉘어 나오게 되며 입력 광자와 출력의 두 광자가 에너지 보존 법칙과 운동량 보존 법칙을 만족하는 조건 하에서 출력 광자가 나오게 된다.<ref>https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion</ref> | |||
]] | ]] | ||
일반적으로 빈 공간상에서 광자끼리는 유의미한 크기의 상호작용을 하지 않는다. | 일반적으로 빈 공간상에서 광자끼리는 유의미한 크기의 상호작용을 하지 않는다. 빔분할기를 이용하여 광자 간 상호작용을 만들어 줄 수 있는데, 비선형 매질을 이용하면 좀 더 다양한 형태의 광자 간 상호작용을 만들어 줄 수 있다. 특히 광자의 파장을 변화시키거나 합치고 나누는 등 광자의 주파수, 즉 에너지를 변환하는 것이 가능하다. 대표적으로 광자 하나를 BBO(Beta Barium Borate)결정과 같은 비선형 매질에 통과시켰을 때, 자발매개하향변환 SPDC(Spontaneous Parametric Down Conversion)으로 알려진 이차 비선형 효과에 의해 높은 주파수의 단일광자가 낮은 주파수이 이광자로 변환되게 되는데 이때 에너지와 운동량 보존 법칙에 따라 생성되는 이광자간 상관관계가 발생된다 (그림 3). 이를 활용하면 편광 또는 주파수 얽힘 광자쌍 생성이 가능하여 양자 광학 실험에서의 중요한 [[양자얽힘]] 광원을 제공하고 있고 항상 동시에 쌍으로 생성된다는 특성을 이용하여, 한쪽 경로의 광자를 측정함으로써 다른쪽에 단일광자가 존재함을 알게되는 예고된 단일광자 광원(heralded single photon)으로써의 활용 또한 가능하다. 비선형 매질로 가장 많이 이용되는 것은 비선형 매질이지만, 원자 기체나 [[양자점]]처럼 광자와 상호작용할 수 있는 다양한 물질들에 대해서도 많은 연구가 이루어지고 있다. | ||
= 개발 현황 = | |||
광자의 2차원 자유도를 활용하는 광자 큐비트의 경우 [[큐비트]]의 인코딩이 용이하기 때문에 광자 큐비트 생성에 대한 연구는 결국 [[얽힘|얽힘상태]] 광자쌍 생성과 같은 양자 광원 연구로 귀결된다.<ref name=Kim>김용수, 조영욱, 광자 큐빗을 이용한 양자연산 기술, Electrical & Electronic Materials '''33''', 16 (2020).</ref> 광원은 보통 손실될 수 있으며, 그러면 원하는 광자가 나타나지 않는다. 광자가 완벽하지 못하면 양자 계산 결과값을 잃을 수 있다. 따라서 완벽한 광자를 만드는 것은 아주 중요한 일이다. | |||
[[File:기술백서 전체수정_92_편집.jpg|left|thumb|300px|그림 4. 준위상 정합(quasi phase matching) AlGaAs 모식도. 파란색과 분홍색 빔은 각각 775nm와 1550nm 파장을 가진 펌프이고 서로 상관관계가 있는 광자를 생성한다.]] | |||
자발 매개하향변환은 수십 년 동안 광자 생성을 위한 방법으로 활용되어왔다. 매개하향변환을 통한 광자쌍 생성 효율은 위상 정합의 정도에 따라 결정된다. 여기에 쓰이는 2차 비선형 물질로는 BBO(Beta Barium Borate), KDP(Potassium Dideuterium Phosphate), AlGaAs 등이 있다. 이 물질들은 위상 정합이 맞지 않는 경우 광자쌍이 생성되지 않거나 생성 효율이 떨어지고 그런 경우 사용이 어렵다. 그러나 주기적 분극(periodic poling)을 통해 위상 정합을 맞춰줄 수 있다.<ref name=Ko>고영호 외 5명, 양자 정보 기술을 위한 양자 광원 연구 동향, 전자통신동향분석 '''34''', 99 (2019). doi:10.22648/ETRI.2019.J.340510</ref> 2002년 MIT에서 주기적 분극 구조인 PPLN(Periodically Poled Lithium Niobate)을 통해 준위상 정합을 얻었으며, 효과적인 광자쌍 생성을 실험적으로 보였다.<ref name=Mason>E. J. Mason, M. A. Albota, F. König and F. N. Wong, Efficient generation of tunable photon pairs at 0.8 and 1.6 µm, Optics Letters '''27''', 002115 (2002). doi:10.1364/OL.27.002115.</ref> 위상 정합을 맞추는 다른 방법으로는 Bragg Grating Reflection을 이용한 광도파로나 Quantum Well Intermixing이 있다. 이는 복굴절이 거의 없는III-V족 반도체를 위한 방법이다. 2012년 캐나다 Waterloo 대학은 준위상 정합 조건을 만족하는 브래그 반사(bragg grating reflection) 광도파로를 통해 광자쌍을 생성하였다.<ref name=Horn>R. Horn, P. Abolghasem, B. J. Bijlani, D. Kang, A. S. Helmy, and G. Weihs, Monolithic source of photon pairs, Physical Review Letters '''108''' , 153605 (2012). doi:10.1103/PhysRevLett.108.153605</ref> 그리고 2013년 캐나다 Toronto 대학에서는 GaAs/AlGaAs의 Quantum Well Intermixing을 통해 준위상 정합을 얻었고 광자쌍을 생성하였다.<ref name=Sarrafi>P. Sarrafi, E. Y. Zhu, K. Dolgaleva, B. M. Holmes, D. C. Hutchings, J. S. Aitchison, and L. Qian, Continuous-wave quasi-phase-matched waveguide correlated photon pair source on a III–V chip, Applied Physics Letters, '''103''' , 251115 (2013). doi:10.1063/1.4851095</ref> | |||
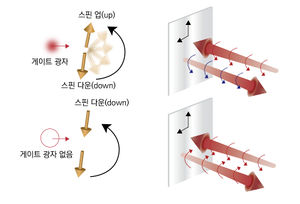
[[File:기술백서 전체수정_93_편집.jpg|right|thumb|300px|그림 5. 단일광자 스위치 및 트랜지스터 작동 원리 모식도. 첫 번째 단계에서 게이트 광자는 스핀의 상태를 제어하고, 두 번째 단계에서 스핀은 신호 필드의 편광도를 결정한다.]] | |||
광자쌍 생성 이외에도 광자 기반 양자컴퓨터에 대한 연구는 진행되어왔다. 2018년 미국의 Maryland 대학에서는 광 공진기와 강하게 결합된 반도체 스핀 큐비트를 이용하여 단일광자 트랜지스터를 시연했다.<ref name=Sun>S. Sun, H. Kim, Z. Luo, G. S. Solomon, and E. Waks, A single-photon switch and transistor enabled by a solid-state quantum memory, Science '''361''', 57 (2018). doi:10.1126/science.aat3581</ref> 이 소자는 대략 매초 100억 개의 광자 큐비트를 빠르게 처리할 수 있다고 기대되었다. 연구팀은 단일광자가 양자점과 상호 작용하여 장치를 통해 두 번째 광 펄스의 전송을 제어할 수 있음을 관찰했다. 첫 번째 광 펄스는 두 번째 광자가 칩에 들어갈 수 있도록 문을 열어준다. 첫 번째 펄스에 광자가 포함되어 있지 않으면 그 양자점은 후속 광자가 통과하지 못하도록 막았다. 연구팀은 양자점의 메모리가 모두 소멸되기 전에 그들의 트랜지스터가 약 30 광자를 포함하는 광 펄스를 전환할 수 있음을 입증했다.<ref>https://scienceon.kisti.re.kr/srch/selectPORSrchTrend.do?cn=GTB2018004219</ref> | |||
그리고 2019년 중국에서는 단일광자 편광 큐비트를 이용한 양자 메모리 실증 실험을 보고했다. 루비듐 원자를 이용하여 만든 이 양자 메모리는 효율이 85%, 신뢰도가 99% 이상이며 최적화할 경우 효율이 90.6%까지 높아질 수 있음을 보였다.<ref name=Wang>Y. Wang, J. Li, S. Zhang, K. Su, Y. Zhou, K. Liao, and S. L. Zhu, Efficient quantum memory for single-photon polarization qubits, Nature Photonics '''13''', 346 (2019).</ref> | |||
최근에는 광자 큐비트와 다른 큐비트를 얽히게 하는 실험도 있었다. 이 연구팀은 질소 공공 전자 스핀 큐비트와 광자 시간-빈 큐비트 사이의 [[양자 얽힘]]의 실현을 보고했다. 이 실험에서 큐비트의 신뢰도는 0.77이었다.<ref name=Tchebotareva>A. Tchebotareva, S. L. Hermans, P. C. Humphreys, C. Voigt, P. J. Harmsma, L. K. Cheng, and R. Hanson, Entanglement between a diamond spin qubit and a photonic time-bin qubit at telecom wavelength, Physical Review Letters '''123''', 063601 (2019). doi:10.1103/PhysRevLett.123.063601</ref> | |||
광자 편광 큐비트를 이용하여 [[CNOT 게이트]]를 시연한 연구 결과도 있었다. 2011년 이 연구팀은 부분 편광 빔분할기의 역할을 하는 통합 장치의 유리 칩에서 제작함으로써, Femtosecond Laser Writing이 수평 및 수직 편광 분할 비율을 제어할 수 있었기에 [[양자 게이트]]를 입증할 수 있었다고 하였다.<ref name=Crespi>A. Crespi, R. Ramponi, R. Osellame, L. Sansoni, I. Bongioanni, F. Sciarrino, and P. Mataloni, Integrated photonic quantum gates for polarization qubits, Nature Communications '''2''', 1 (2011). doi:10.1038/ncomms1570.</ref> | |||
= 참고 문헌 = | = 참고 문헌 = | ||
2021년 12월 2일 (목) 01:22 기준 최신판
<양자 기술백서 |
개요[편집]
양자컴퓨팅에서 광자는 큐비트의 주요 구현 방식 중 하나로 연구되고 있으며, 뚜렷한 장점, 즉 특별히 상호작용하는 물질과 접촉하지 않는 이상 환경과 상호작용을 잘 하지 않아 결맞음이 오래 유지된다는 특성이 있다. 또한 이러한 결맞음 특성과 함께 빛의 속도로 빠르게 이동한다는 특성상 멀리 보내기도 수월하다는 장점을 가지고 있다. 이러한 점 때문에 광자는 양자컴퓨팅뿐 아니라 양자통신에서 활발하게 연구되고 있는 주제이기도 하다. 또한 광자 큐비트는 기존의 벌크, 광섬유 기반의 광학 기구를 이용하여 양자 상태를 제어하기에 다른 플랫폼에 비해 시스템 구축이 용이하다는 장점도 가지고 있다.
반면에 이러한 특성은 광자 기반 양자컴퓨터의 약점으로 꼽히기도 한다. 광자 간 상호작용은 물론이고 다른 물질을 이용하여 광자의 주파수를 변환하는 비선형 변환의 경우 상호작용 정도가 매우 약하기 때문에 결정론적인 게이트를 만들기 어렵고 확률적인 게이트를 사용할 수밖에 없는 경우가 많다. 또한 이러한 약한 상호작용의 특성과 맞물려 대량의 광자를 얽힘 상태로 만드는 것이 어렵다는 점도 하나의 특징으로 꼽히고 있다. 현재까지 얽힘 상태로 가장 많은 수의 광자를 생성한 것으로 12 광자 얽힘 상태가 알려져 있다 (그림 1 참고).[1]
양자 광학[편집]
큐비트[편집]
광자란 일반적인 의미로, 빛으로서 최소 단위 에너지를 갖는 알갱이이다. 광자 기반 양자컴퓨팅에 사용되는 큐비트로는, 광자의 다양한 자유도를 이용한 여러가지 종류가 있다. 우선 선편광 중 한 축의 편광과 그에 수직한 다른 편광을 사용하는 방법이 있다. 선편광된 광자는 편광판이나 편광 빔분할기를 이용해 쉽게 만들 수 있고, 반파장판을 이용해 편광의 각도를 회전시킬 수 있으며, 다시 편광판과 측정기의 조합을 이용해 특정 편광을 측정할 수 있는 등, 큐비트 조작이 용이하기 때문에 광자 기반 양자컴퓨팅 및 기타 광자 관련 실험에 널리 쓰인다. 편광 방향은 일반적으로 광평면에 수평한 수평 방향 편광 $$\left| H \right\rangle$$ 와 그에 수직한 수직방향 편광 $$\left| V \right\rangle$$ 를 많이 사용한다. 이 경우 광자 큐비트 상태 $$\left| \psi \right\rangle$$ 는,
\[\left| \psi \right\rangle= \alpha\left| H \right\rangle + \beta\left| V \right\rangle\]
로 표현할 수 있다 (여기서 $$\alpha, \beta$$ 는 $$|\alpha|^{2} + |\beta|^{2}= 1$$ 인 복소수). 그 밖에 서로 다른 두 주파수를 큐비트의 두 상태로 정하고 이 두 주파수와 반응하는 원자나 결정을 사용하여 큐비트 조작을 하는 방법, 두 개의 공진기나 경로를 만들어놓고 광자가 둘 중 어느 쪽에 있는지를 큐비트의 상태로 이용하는 방법, 궤도 각운동량을 큐비트로써 이용하는 방법 등이 있다.
결맞음 상태 (Coherent State)[편집]
결맞음 상태란, 소멸 연산자(annihilation operator) $$\widehat{a}$$ 의 고유 상태, 즉
\[\widehat{a}\left| \alpha \right\rangle= \alpha\left| \alpha \right\rangle\]
의 $$\left| \alpha \right\rangle$$ 으로 정의된다. 이 때 $$\alpha= |\alpha|e^{\text{iθ}}$$ 로 나타냈을 때 $$|\alpha|$$는 진폭, $$\theta$$는 위상이라고 부른다. 이는 고전역학에서의 조화 진동자에 있는 입자의 상태를 양자역학적으로 해석할 때 사용하기 위해 고안된 상태로, 위상공간에서는 그림 2와 같이 나타낼 수 있다. X와 P는 위상공간의 축을 만드는 쿼드러처이며, 진폭과 위상은 각각 불확정성을 갖고 있다.[3] 결맞음 상태의 중요한 특징 중 하나는, 이 상태가 최소 불확정성 상태, 즉 $$\Delta X= \Delta P =1/2$$ 라는 점이다. 여기서 $$\text{ΔX}$$, $$\text{ΔP}$$ 또는 임의의 쿼드러처로의 불확정성을 줄이는 대신 다른 쿼드러처의 불확정성을 높인 조임 상태를 만들 수도 있다.
조임 상태 (Squeezed State)[편집]
결맞음 상태에서 하나의 쿼드러처로 불확정성을 줄인 상태를 조임상태라고 한다. 이 때 $$\Delta X\Delta P > 1/4$$ 가 되며, 양자광학에서는 일반적으로 두 광자의 조임 정도가 이 둘의 양자 얽힘 정도와 관련이 있기 때문에 중요하게 다루어진다.[4]
광학 기구[편집]
빔분할기 (Beam Splitter)[편집]
빔분할기는 고전광학적으로는 빔을 일정 비율의 출력으로 나눠서 서로 다른 경로로 보내주는 장치이다. 그러나 양자광학적으로는, 단일광자에 대해 출력을 나누는 것은 불가능하기 때문에 확률적으로 경로가 선택되게 된다. 입력 모드 $${\widehat{a}}_{0}$$, $${\widehat{a}}_{1}$$ 과 출력 모드 $${\widehat{a}}_{2}$$, $${\widehat{a}}_{3}$$ 에 대해 다음과 같이 변환 관계로 나타낼 수 있으며, 이에 따라 확률진폭이 나눠지게 된다.
\[\begin{pmatrix} {\widehat{a}}_{2} \\ {\widehat{a}}_{3} \\ \end{pmatrix}= \begin{pmatrix} t^{'} & r \\ r^{'} & t \\ \end{pmatrix} \begin{pmatrix} {\widehat{a}}_{0} \\ {\widehat{a}}_{1} \\ \end{pmatrix}\]
50:50 빔분할기의 경우 반사빔과 투과빔이 $$e^{\pm i\frac{\pi}{2}}=\pm i= cos(\frac{\pi}{2})\pm isin(\frac{\pi}{2})$$의 위상차가 발생한다. 투과빔이 $${+\frac{\pi}{2}}$$의 위상차를 가진다고 가정했을 때, 입력모드와 출력모드의 관계는 다음과 같다.
\[{\widehat{a}}_{2}= \frac{1}{\sqrt{2}}\left({\widehat{a}}_{0} + i{\widehat{a}}_{1} \right), {\widehat{a}}_{3} =\frac{1}{\sqrt{2}}\left( i{\widehat{a}}_{0} + {\widehat{a}}_{1} \right)\]
위상 변조기 (Phase Shifter)[편집]
광자의 진행을 늦춤으로서 위상을 변화시키는 장치이다. 빛의 속도를 느리게 하는 물질을 이용하거나, 단순히 액츄에이터 등을 사용해서 경로의 길이를 변화시킴으로써 위상 변화를 만들어줄 수 있다. 양자컴퓨팅에서는, 큐비트를 이루는 두 모드 간의 위상 변화는 곧 큐비트의 국소 위상을 변화시키는 것이기 때문에, 광자 큐비트의 제어에서 필수 부품이라고 할 수 있다.
비선형 매질 (Nonlinear Medium)[편집]
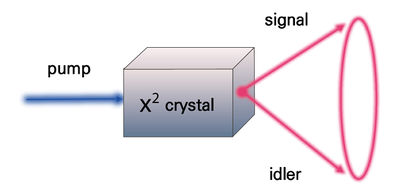
일반적으로 빈 공간상에서 광자끼리는 유의미한 크기의 상호작용을 하지 않는다. 빔분할기를 이용하여 광자 간 상호작용을 만들어 줄 수 있는데, 비선형 매질을 이용하면 좀 더 다양한 형태의 광자 간 상호작용을 만들어 줄 수 있다. 특히 광자의 파장을 변화시키거나 합치고 나누는 등 광자의 주파수, 즉 에너지를 변환하는 것이 가능하다. 대표적으로 광자 하나를 BBO(Beta Barium Borate)결정과 같은 비선형 매질에 통과시켰을 때, 자발매개하향변환 SPDC(Spontaneous Parametric Down Conversion)으로 알려진 이차 비선형 효과에 의해 높은 주파수의 단일광자가 낮은 주파수이 이광자로 변환되게 되는데 이때 에너지와 운동량 보존 법칙에 따라 생성되는 이광자간 상관관계가 발생된다 (그림 3). 이를 활용하면 편광 또는 주파수 얽힘 광자쌍 생성이 가능하여 양자 광학 실험에서의 중요한 양자얽힘 광원을 제공하고 있고 항상 동시에 쌍으로 생성된다는 특성을 이용하여, 한쪽 경로의 광자를 측정함으로써 다른쪽에 단일광자가 존재함을 알게되는 예고된 단일광자 광원(heralded single photon)으로써의 활용 또한 가능하다. 비선형 매질로 가장 많이 이용되는 것은 비선형 매질이지만, 원자 기체나 양자점처럼 광자와 상호작용할 수 있는 다양한 물질들에 대해서도 많은 연구가 이루어지고 있다.
개발 현황[편집]
광자의 2차원 자유도를 활용하는 광자 큐비트의 경우 큐비트의 인코딩이 용이하기 때문에 광자 큐비트 생성에 대한 연구는 결국 얽힘상태 광자쌍 생성과 같은 양자 광원 연구로 귀결된다.[6] 광원은 보통 손실될 수 있으며, 그러면 원하는 광자가 나타나지 않는다. 광자가 완벽하지 못하면 양자 계산 결과값을 잃을 수 있다. 따라서 완벽한 광자를 만드는 것은 아주 중요한 일이다.
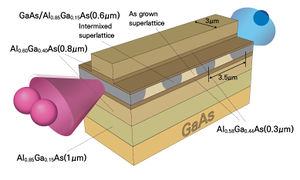
자발 매개하향변환은 수십 년 동안 광자 생성을 위한 방법으로 활용되어왔다. 매개하향변환을 통한 광자쌍 생성 효율은 위상 정합의 정도에 따라 결정된다. 여기에 쓰이는 2차 비선형 물질로는 BBO(Beta Barium Borate), KDP(Potassium Dideuterium Phosphate), AlGaAs 등이 있다. 이 물질들은 위상 정합이 맞지 않는 경우 광자쌍이 생성되지 않거나 생성 효율이 떨어지고 그런 경우 사용이 어렵다. 그러나 주기적 분극(periodic poling)을 통해 위상 정합을 맞춰줄 수 있다.[7] 2002년 MIT에서 주기적 분극 구조인 PPLN(Periodically Poled Lithium Niobate)을 통해 준위상 정합을 얻었으며, 효과적인 광자쌍 생성을 실험적으로 보였다.[8] 위상 정합을 맞추는 다른 방법으로는 Bragg Grating Reflection을 이용한 광도파로나 Quantum Well Intermixing이 있다. 이는 복굴절이 거의 없는III-V족 반도체를 위한 방법이다. 2012년 캐나다 Waterloo 대학은 준위상 정합 조건을 만족하는 브래그 반사(bragg grating reflection) 광도파로를 통해 광자쌍을 생성하였다.[9] 그리고 2013년 캐나다 Toronto 대학에서는 GaAs/AlGaAs의 Quantum Well Intermixing을 통해 준위상 정합을 얻었고 광자쌍을 생성하였다.[10]
광자쌍 생성 이외에도 광자 기반 양자컴퓨터에 대한 연구는 진행되어왔다. 2018년 미국의 Maryland 대학에서는 광 공진기와 강하게 결합된 반도체 스핀 큐비트를 이용하여 단일광자 트랜지스터를 시연했다.[11] 이 소자는 대략 매초 100억 개의 광자 큐비트를 빠르게 처리할 수 있다고 기대되었다. 연구팀은 단일광자가 양자점과 상호 작용하여 장치를 통해 두 번째 광 펄스의 전송을 제어할 수 있음을 관찰했다. 첫 번째 광 펄스는 두 번째 광자가 칩에 들어갈 수 있도록 문을 열어준다. 첫 번째 펄스에 광자가 포함되어 있지 않으면 그 양자점은 후속 광자가 통과하지 못하도록 막았다. 연구팀은 양자점의 메모리가 모두 소멸되기 전에 그들의 트랜지스터가 약 30 광자를 포함하는 광 펄스를 전환할 수 있음을 입증했다.[12]
그리고 2019년 중국에서는 단일광자 편광 큐비트를 이용한 양자 메모리 실증 실험을 보고했다. 루비듐 원자를 이용하여 만든 이 양자 메모리는 효율이 85%, 신뢰도가 99% 이상이며 최적화할 경우 효율이 90.6%까지 높아질 수 있음을 보였다.[13]
최근에는 광자 큐비트와 다른 큐비트를 얽히게 하는 실험도 있었다. 이 연구팀은 질소 공공 전자 스핀 큐비트와 광자 시간-빈 큐비트 사이의 양자 얽힘의 실현을 보고했다. 이 실험에서 큐비트의 신뢰도는 0.77이었다.[14]
광자 편광 큐비트를 이용하여 CNOT 게이트를 시연한 연구 결과도 있었다. 2011년 이 연구팀은 부분 편광 빔분할기의 역할을 하는 통합 장치의 유리 칩에서 제작함으로써, Femtosecond Laser Writing이 수평 및 수직 편광 분할 비율을 제어할 수 있었기에 양자 게이트를 입증할 수 있었다고 하였다.[15]
참고 문헌[편집]
- ↑ 1.0 1.1 H. S. Zhong, Y. Li, W. Li,L. C. Peng,Z. E. Su, Y. Hu, L. Zhang, 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion, Physical Review Letters 121, 250505 (2018). doi:10.1103/PhysRevLett.121.250505.
- ↑ https://en.wikipedia.org/wiki/Coherent_states
- ↑ S. Olivares, Quantum optics in the phase space, The European Physical Journal Special Topics 203 (2012). doi:10.1140/epjst/e2012-01532-4.
- ↑ P. Marek, M. Paternostro, & M. S. Kim, Characterization of the entanglement of two squeezed states, Physical Review A 74, 032311 (2006)
- ↑ https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
- ↑ 김용수, 조영욱, 광자 큐빗을 이용한 양자연산 기술, Electrical & Electronic Materials 33, 16 (2020).
- ↑ 고영호 외 5명, 양자 정보 기술을 위한 양자 광원 연구 동향, 전자통신동향분석 34, 99 (2019). doi:10.22648/ETRI.2019.J.340510
- ↑ E. J. Mason, M. A. Albota, F. König and F. N. Wong, Efficient generation of tunable photon pairs at 0.8 and 1.6 µm, Optics Letters 27, 002115 (2002). doi:10.1364/OL.27.002115.
- ↑ R. Horn, P. Abolghasem, B. J. Bijlani, D. Kang, A. S. Helmy, and G. Weihs, Monolithic source of photon pairs, Physical Review Letters 108 , 153605 (2012). doi:10.1103/PhysRevLett.108.153605
- ↑ P. Sarrafi, E. Y. Zhu, K. Dolgaleva, B. M. Holmes, D. C. Hutchings, J. S. Aitchison, and L. Qian, Continuous-wave quasi-phase-matched waveguide correlated photon pair source on a III–V chip, Applied Physics Letters, 103 , 251115 (2013). doi:10.1063/1.4851095
- ↑ S. Sun, H. Kim, Z. Luo, G. S. Solomon, and E. Waks, A single-photon switch and transistor enabled by a solid-state quantum memory, Science 361, 57 (2018). doi:10.1126/science.aat3581
- ↑ https://scienceon.kisti.re.kr/srch/selectPORSrchTrend.do?cn=GTB2018004219
- ↑ Y. Wang, J. Li, S. Zhang, K. Su, Y. Zhou, K. Liao, and S. L. Zhu, Efficient quantum memory for single-photon polarization qubits, Nature Photonics 13, 346 (2019).
- ↑ A. Tchebotareva, S. L. Hermans, P. C. Humphreys, C. Voigt, P. J. Harmsma, L. K. Cheng, and R. Hanson, Entanglement between a diamond spin qubit and a photonic time-bin qubit at telecom wavelength, Physical Review Letters 123, 063601 (2019). doi:10.1103/PhysRevLett.123.063601
- ↑ A. Crespi, R. Ramponi, R. Osellame, L. Sansoni, I. Bongioanni, F. Sciarrino, and P. Mataloni, Integrated photonic quantum gates for polarization qubits, Nature Communications 2, 1 (2011). doi:10.1038/ncomms1570.