공통 기술: 두 판 사이의 차이
| (사용자 5명의 중간 판 29개는 보이지 않습니다) | |||
| 5번째 줄: | 5번째 줄: | ||
┗|[[초전도 큐비트 (Superconducting Qubit)]]> | ┗|[[초전도 큐비트 (Superconducting Qubit)]]> | ||
= 개요 (Introduction) = | |||
기존의 컴퓨터는 0 또는 1을 논리값으로 갖는 비트를 기본적인 데이터의 단위로 사용하는데 반해 양자컴퓨터는 0과 1은 물론 이들 사이의 중첩을 포함하는 큐비트를 사용한다. 우리가 양자컴퓨터를 사용하기 위해선 다수의 큐비트를 만들고, 원하는 연산을 수행하고, 양자상태를 측정하는 기술이 필요하다. 유용한 양자컴퓨터를 만들기 위해서는 이러한 큐비트 생성, 제어, 측정을 충분히 작은 오류를 가진 많은 수의 큐비트에서 구현해야 한다. | |||
큐비트는 2차원 양자상태이므로, 다양한 물리계를 양자컴퓨터 구현에 이용할 수 있지만, 크게 동적 큐비트(Flying qubit)와 정적 큐비트(Stationary qubit)로 나눌 수 있다. 동적 큐비트는 큐비트를 멀리 보내기 용이한 물리계로 구현할 수 있는데, 흔히 광자를 이용해 구현할 수 있다. 정적 큐비트는 한 자리에 머물러 있어 양자연산을 구현하기 용이한 물리계로 구현할 수 있는데, 광자 이외의 대부분 물리계가 여기에 해당한다. 동적 큐비트는 정적 큐비트와는 특성이 매우 달라 양자상태를 생성, 측정, 제어하는 방법이 매우 독특한데, 이에대한 내용은 후에 광자 큐비트에서 다룬다. 정적 큐비트 역시 다양한 방법으로 구현할 수 있지만, 특히 에너지 준위를 0과 1로 이용하는 방법이 널리 이용된고 있다. 이후 기술될 내용은 이러한 에너지 준위 기반 큐비트에 공통적으로 적용되는 기술들이다. | |||
= 라비 진동 (Rabi Oscillation) = | = 라비 진동 (Rabi Oscillation) = | ||
[[File: | [[File:Rabi oscillation 수정.png|thumb|none|350px|그림 1. 시간에 따른 [[큐비트]]의 양자상태 전이 확률 (라비진동)<ref>Rabi cycle, Wikipedia (https://en.wikipedia.org/wiki/Rabi_cycle)</ref>. 주파수 차이(Detuning) Δ에 따른 라비 진동의 진폭 및 주기 변화를 볼 수 있다. $$\Omega_{0}$$는 라비 진동수이다.]] | ||
이준위 원자(two-level atom)가 | 이준위 원자(two-level atom)가 전자기파에 노출되었을 때 원자의 전이 진동수와 전자기파가 공명하면 원자가 광자를 흡수하여 바닥상태에서 들뜬 상태로 전이하게 되고, 또 다른 광자가 조명될 때 원자는 전자기파와 동일한 위상과 진동수를 가진 전자기파를 방출하게 된다. 이를 유도방출이라 한다. 이 주기적으로 흡수, 유도방출하는 현상을 라비 진동(Rabi Oscillation)이라고 하며, 이를 이용해 큐비트 상태 $$|0\rangle$$과 $$|1\rangle$$의 확률진폭을 조절할 수 있다. 라비 진동 주파수는 전자기장의 세기가 클수록 빨라지고, 전자기장의 주파수가 원자의 공명 주파수에 가까울수록 느리게 된다. | ||
원자뿐만 아니라 앞으로 서술될 여러 [[큐비트]] 플랫폼에서도 에너지 준위로 기술되는 양자상태를 제어해주는 전자기파가 같은 원리로 작동하는 것으로 이해할 수 있다. | 원자뿐만 아니라 앞으로 서술될 여러 [[큐비트]] 플랫폼에서도 에너지 준위로 기술되는 양자상태를 제어해주는 전자기파가 같은 원리로 작동하는 것으로 이해할 수 있다. | ||
= [[큐비트]] | = [[큐비트]] 제어 (Qubit Control) = | ||
[[큐비트]]의 | [[큐비트]]의 제어는 라비 진동을 기반으로 이루어진다. [[큐비트]]의 두 준위의 차와 공명하는 전자기장을 조사하게 되면 라비 진동을 보이게 된다. 이 전자기장의 조사 시간을 변경하면 큐비트의 상태를 제어할 수 있다. | ||
예를 들어 라비 진동의 $$\pi$$ 주기에 해당하는 시간만큼 전자기장을 조사하게 되면 [[큐비트]]의 상태를 반전시킬 수 있는데, $$\left| \left. 0 \right\rangle \right. $$ 인 상태를 $$\left| \left. 1 \right\rangle \right. $$로, $$\left| \left. 1 \right\rangle \right. $$ 인 경우는 $$\left| \left. 0 \right\rangle \right. $$으로 만들게 된다. 이는 파울리 행렬의 $$\sigma_{x}$$에 해당하는 변환이다. 같은 방법으로 조사하는 전자기장의 시간을 제어하면 [[큐비트]]의 [[양자 중첩(superposition)]] 상태 또한 만들 수 있다. | 예를 들어 라비 진동의 $$\pi$$ 주기에 해당하는 시간만큼 전자기장을 조사하게 되면 [[큐비트]]의 상태를 반전시킬 수 있는데, $$\left| \left. 0 \right\rangle \right. $$ 인 상태를 $$\left| \left. 1 \right\rangle \right. $$로, $$\left| \left. 1 \right\rangle \right. $$ 인 경우는 $$\left| \left. 0 \right\rangle \right. $$으로 만들게 된다. 이는 파울리 행렬의 $$\sigma_{x}$$에 해당하는 변환이다. 같은 방법으로 조사하는 전자기장의 시간을 제어하면 [[큐비트]]의 [[양자 중첩(superposition)]] 상태 또한 만들 수 있다. | ||
[[큐비트]]를 | [[큐비트]]를 제어하는 전자기장의 위상을 조작하여 블로흐 구(Bloch sphere)로 표현할 수 있는 [[큐비트]]의 위상을 제어할 수 있다. $$\sigma_{x}$$에 해당하는 전자기파와 90도 차이나는 제어 펄스를 조사하게 되면 $$\sigma_{y}$$변환을 할 수 있다. 또한 주파수를 변경하여 블로흐 구(Bloch sphere)에서 [[큐비트]]의 위상만 변경하는 $$\sigma_{z}$$변환을 할 수 있다. 이로써 기본적인 파울리 행렬에 해당하는 [[큐비트]] 조작이 가능하고 이는 양자 컴퓨팅을 위한 가장 기본적인 유니타리 (unitary) 연산(unitary operation)이라고 할 수 있다. | ||
= 람지 측정 (Ramsey Measurement) = | = 람지 측정 (Ramsey Measurement) = | ||
[[File: | [[File:Ramsey measurement 수정.png|none|thumb|700px|그림 2. 람지 측정 (Ramsey measurement). (위) 람지 측정 방법의 개요도와 블로흐 구(Bloch sphere)에서의 큐비트 상태. 두 개의 π/2 펄스와 기다리는 시간으로 구성되어 있다. (아래) 실험적으로 관측된 람지 측정 결과<ref name=Wynands>R. Wynands. and S. Weyers, Atomic fountain clocks, Metrologia '''42(3)''', S64 (2005), doi:10.1088/0026-1394/42/3/S08.</ref>.]] | ||
[[큐비트]]의 공명 주파수를 정밀하게 측정하는 방법이다. 두개의 준위 $$\left| \left. 0 \right\rangle \right. $$과 $$\left| \left. 1 \right\rangle \right. $$을 갖는 큐비트와 외부에서 조사하는 전자기파를 생각해 보자. 큐비트의 $$\left| \left. 0 \right\rangle \right. $$과 $$\left| \left. 1 \right\rangle \right. $$ 사이의 전이 확률은 전자기파의 주파수가 공명 주파수와 일치할 경우 가장 크다. 이는 라비 진동을 통해 구할 수도 있으나, Ramsey | [[큐비트]]의 공명 주파수를 정밀하게 측정하는 방법이다. 1) 양자 센서를 초기화 한다. 2) $$\frac{\pi}{2}$$ pulse를 가해서 양자 상태 $$\left| \psi_{0} \right\rangle$$에 있도록 준비한다. 3) ''t''초 동안 외부 포텐셜을 제거한 $$H_{0}$$ 해밀토니안을 가한다. 4) 다시 $$\frac{\pi}{2}$$를 가한다. 5) 측정을 한다. 두개의 준위 $$\left| \left. 0 \right\rangle \right. $$과 $$\left| \left. 1 \right\rangle \right. $$을 갖는 큐비트와 외부에서 조사하는 전자기파를 생각해 보자. 큐비트의 $$\left| \left. 0 \right\rangle \right. $$과 $$\left| \left. 1 \right\rangle \right. $$ 사이의 전이 확률은 전자기파의 주파수가 공명 주파수와 일치할 경우 가장 크다. 이는 라비 진동을 통해 구할 수도 있으나, 람지 간섭계(Ramsey interferometry)를 이용하면 더 정밀(precise)하고 정확(accurate)하게 측정할 수 있다. | ||
람지 측정(Ramsey measurement)은 두 개의 $$\frac{\pi}{2}$$ 펄스와 펄스 사이의 기다리는 시간으로 구성되어 있다. 펄스의 주파수를 변경하면서 원자의 에너지 상태를 측정하게 되면 | 람지 측정(Ramsey measurement)은 두 개의 $$\frac{\pi}{2}$$ 펄스와 펄스 사이의 기다리는 시간으로 구성되어 있다. 펄스의 주파수를 변경하면서 원자의 에너지 상태를 측정하게 되면 주파수 축에 대하여 간섭무늬의 결과를 얻게 되고, 이는 단순히 외부 전자기장의 주파수를 주사(scan)하는 방법보다 더 정밀하게 공명 주파수를 측정할 수 있으며 전자기장 자체로부터 오는 [[측정 오차(AC Stark shift)]]를 줄일 수 있다. | ||
= 스핀 메아리 (Spin Echo) = | = 스핀 메아리 (Spin Echo) = | ||
[[File: | [[File:Spin echo 수정.png|none|thumb|700px|그림 3. 스핀 메아리(spin echo)<ref>Spin echo, Wikipedia (https://en.wikipedia.org/wiki/Spin_echo)</ref>. A) 큐비트를 초기화 한다. B) 90도 펄스를 이용하여 양자 중첩 상태로 만든다. C) 시간 t 만큼 기다린다. 위상이 변하게 된다. D) 180도 펄스를 이용하여 상태를 뒤집는다. E) 시간 t 만큼 기다린다. F) 강한 메아리 신호를 관측할 수 있다.]] | ||
핵의 스핀 자기 공명에서 처음 개발된 기술로, 사용하는 전자기파 펄스를 적당한 시간 간격을 두고 2번 조사하면 이 시간 간격 후에 강한 신호가 관측된다. 이 신호가 메아리(echo)처럼 응답하므로 스핀 메아리(Spin echo)라고 한다. 이는 핵 스핀에서만 적용되지 않고, 전자 스핀계, 포톤, 포논 등에 대해서도 작용하는 것이 관측되었다. 양자정보과학에 널리 사용하는 기술로서 [[큐비트]]의 상태를 회복하는데 사용되고 있다. | 핵의 스핀 자기 공명에서 처음 개발된 기술로, 사용하는 전자기파 펄스를 적당한 시간 간격을 두고 2번 조사하면 이 시간 간격 후에 강한 신호가 관측된다. 이 신호가 메아리(echo)처럼 응답하므로 스핀 메아리(Spin echo)라고 한다. 이는 핵 스핀에서만 적용되지 않고, 전자 스핀계, 포톤, 포논 등에 대해서도 작용하는 것이 관측되었다. 양자정보과학에 널리 사용하는 기술로서 [[큐비트]]의 상태를 회복하는데 사용되고 있다. | ||
스핀 메아리의 개수 및 다른 위상의 펄스를 연속적으로 적용하여 양자 상태의 [[결맞음 시간]]을 증가시키는 다양한 방법들이 고안되었다. 이를 Dynamical decoupling (DD)이라고 하며, Knill DD (KDD), CPMG(Carr-Purcell-Meiboom-Gill), Uhrig DD(UDD), periodic DD(PDD)등 다양한 펄스 적용 방법들이 있다. | 스핀 메아리의 개수 및 다른 위상의 펄스를 연속적으로 적용하여 양자 상태의 [[결맞음 시간]]을 증가시키는 다양한 방법들이 고안되었다. 이를 동역학적 짝풀림(Dynamical decoupling) (DD)이라고 하며, Knill DD (KDD), CPMG(Carr-Purcell-Meiboom-Gill), Uhrig DD(UDD), periodic DD(PDD)등 다양한 펄스 적용 방법들이 있다. | ||
= AC 슈타르크 이동 (AC Stark Shift | = AC 슈타르크 이동 (AC Stark Shift) = | ||
[[File: | [[File:AC stark shift 수정.png|none|thumb|300px|그림 4. A.C. Stark Shift. 전자기장에 의해 원자가 섭동할 경우(Perturbed) 섭동하지 않은 상태(Unperturbed)에 비해 에너지 레벨이 변하게 된다. | ||
]] | ]] | ||
원자가 전자기장에 있을 경우 그 상태가 전자기장에 | 원자가 전자기장에 있을 경우 그 고유 에너지 상태가 전자기장에 의해 섭동하지 않을 경우에 비해 $$\pm \Omega^{2}/4\delta$$ 만큼 변하게 되는데 이를 a.c. Stark Shift라고 한다. Ω는 라비 진동으로 레이저의 세기를 의미하고, δ는 레이저와 원자의 에너지 레벨의 주파수 차이를 의미한다. 이는 광격자(Optical lattices)를 포함한 광 포획 기술의 원리가 된다. 또한 레이저 및 전자기장을 이용한 [[큐비트]] 조작 시 에너지 레벨을 변경시키는 원인이 되므로 공명 주파수를 사용할 때 충분히 고려해야 된다. | ||
= 참고 문헌 = | = 참고 문헌 = | ||
2021년 12월 29일 (수) 15:19 기준 최신판
<양자 기술백서 |
┗|초전도 큐비트 (Superconducting Qubit)>
개요 (Introduction)[편집]
기존의 컴퓨터는 0 또는 1을 논리값으로 갖는 비트를 기본적인 데이터의 단위로 사용하는데 반해 양자컴퓨터는 0과 1은 물론 이들 사이의 중첩을 포함하는 큐비트를 사용한다. 우리가 양자컴퓨터를 사용하기 위해선 다수의 큐비트를 만들고, 원하는 연산을 수행하고, 양자상태를 측정하는 기술이 필요하다. 유용한 양자컴퓨터를 만들기 위해서는 이러한 큐비트 생성, 제어, 측정을 충분히 작은 오류를 가진 많은 수의 큐비트에서 구현해야 한다.
큐비트는 2차원 양자상태이므로, 다양한 물리계를 양자컴퓨터 구현에 이용할 수 있지만, 크게 동적 큐비트(Flying qubit)와 정적 큐비트(Stationary qubit)로 나눌 수 있다. 동적 큐비트는 큐비트를 멀리 보내기 용이한 물리계로 구현할 수 있는데, 흔히 광자를 이용해 구현할 수 있다. 정적 큐비트는 한 자리에 머물러 있어 양자연산을 구현하기 용이한 물리계로 구현할 수 있는데, 광자 이외의 대부분 물리계가 여기에 해당한다. 동적 큐비트는 정적 큐비트와는 특성이 매우 달라 양자상태를 생성, 측정, 제어하는 방법이 매우 독특한데, 이에대한 내용은 후에 광자 큐비트에서 다룬다. 정적 큐비트 역시 다양한 방법으로 구현할 수 있지만, 특히 에너지 준위를 0과 1로 이용하는 방법이 널리 이용된고 있다. 이후 기술될 내용은 이러한 에너지 준위 기반 큐비트에 공통적으로 적용되는 기술들이다.
라비 진동 (Rabi Oscillation)[편집]
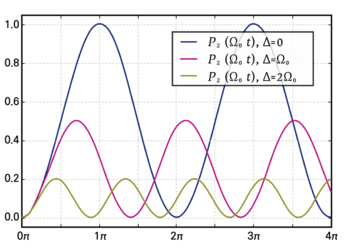
이준위 원자(two-level atom)가 전자기파에 노출되었을 때 원자의 전이 진동수와 전자기파가 공명하면 원자가 광자를 흡수하여 바닥상태에서 들뜬 상태로 전이하게 되고, 또 다른 광자가 조명될 때 원자는 전자기파와 동일한 위상과 진동수를 가진 전자기파를 방출하게 된다. 이를 유도방출이라 한다. 이 주기적으로 흡수, 유도방출하는 현상을 라비 진동(Rabi Oscillation)이라고 하며, 이를 이용해 큐비트 상태 $$|0\rangle$$과 $$|1\rangle$$의 확률진폭을 조절할 수 있다. 라비 진동 주파수는 전자기장의 세기가 클수록 빨라지고, 전자기장의 주파수가 원자의 공명 주파수에 가까울수록 느리게 된다.
원자뿐만 아니라 앞으로 서술될 여러 큐비트 플랫폼에서도 에너지 준위로 기술되는 양자상태를 제어해주는 전자기파가 같은 원리로 작동하는 것으로 이해할 수 있다.
큐비트 제어 (Qubit Control)[편집]
큐비트의 제어는 라비 진동을 기반으로 이루어진다. 큐비트의 두 준위의 차와 공명하는 전자기장을 조사하게 되면 라비 진동을 보이게 된다. 이 전자기장의 조사 시간을 변경하면 큐비트의 상태를 제어할 수 있다.
예를 들어 라비 진동의 $$\pi$$ 주기에 해당하는 시간만큼 전자기장을 조사하게 되면 큐비트의 상태를 반전시킬 수 있는데, $$\left| \left. 0 \right\rangle \right. $$ 인 상태를 $$\left| \left. 1 \right\rangle \right. $$로, $$\left| \left. 1 \right\rangle \right. $$ 인 경우는 $$\left| \left. 0 \right\rangle \right. $$으로 만들게 된다. 이는 파울리 행렬의 $$\sigma_{x}$$에 해당하는 변환이다. 같은 방법으로 조사하는 전자기장의 시간을 제어하면 큐비트의 양자 중첩(superposition) 상태 또한 만들 수 있다.
큐비트를 제어하는 전자기장의 위상을 조작하여 블로흐 구(Bloch sphere)로 표현할 수 있는 큐비트의 위상을 제어할 수 있다. $$\sigma_{x}$$에 해당하는 전자기파와 90도 차이나는 제어 펄스를 조사하게 되면 $$\sigma_{y}$$변환을 할 수 있다. 또한 주파수를 변경하여 블로흐 구(Bloch sphere)에서 큐비트의 위상만 변경하는 $$\sigma_{z}$$변환을 할 수 있다. 이로써 기본적인 파울리 행렬에 해당하는 큐비트 조작이 가능하고 이는 양자 컴퓨팅을 위한 가장 기본적인 유니타리 (unitary) 연산(unitary operation)이라고 할 수 있다.
람지 측정 (Ramsey Measurement)[편집]
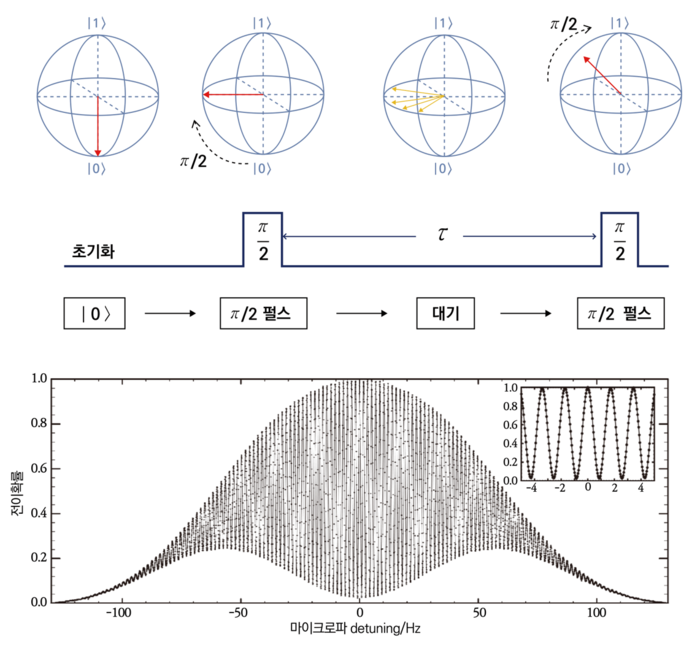
큐비트의 공명 주파수를 정밀하게 측정하는 방법이다. 1) 양자 센서를 초기화 한다. 2) $$\frac{\pi}{2}$$ pulse를 가해서 양자 상태 $$\left| \psi_{0} \right\rangle$$에 있도록 준비한다. 3) t초 동안 외부 포텐셜을 제거한 $$H_{0}$$ 해밀토니안을 가한다. 4) 다시 $$\frac{\pi}{2}$$를 가한다. 5) 측정을 한다. 두개의 준위 $$\left| \left. 0 \right\rangle \right. $$과 $$\left| \left. 1 \right\rangle \right. $$을 갖는 큐비트와 외부에서 조사하는 전자기파를 생각해 보자. 큐비트의 $$\left| \left. 0 \right\rangle \right. $$과 $$\left| \left. 1 \right\rangle \right. $$ 사이의 전이 확률은 전자기파의 주파수가 공명 주파수와 일치할 경우 가장 크다. 이는 라비 진동을 통해 구할 수도 있으나, 람지 간섭계(Ramsey interferometry)를 이용하면 더 정밀(precise)하고 정확(accurate)하게 측정할 수 있다.
람지 측정(Ramsey measurement)은 두 개의 $$\frac{\pi}{2}$$ 펄스와 펄스 사이의 기다리는 시간으로 구성되어 있다. 펄스의 주파수를 변경하면서 원자의 에너지 상태를 측정하게 되면 주파수 축에 대하여 간섭무늬의 결과를 얻게 되고, 이는 단순히 외부 전자기장의 주파수를 주사(scan)하는 방법보다 더 정밀하게 공명 주파수를 측정할 수 있으며 전자기장 자체로부터 오는 측정 오차(AC Stark shift)를 줄일 수 있다.
스핀 메아리 (Spin Echo)[편집]
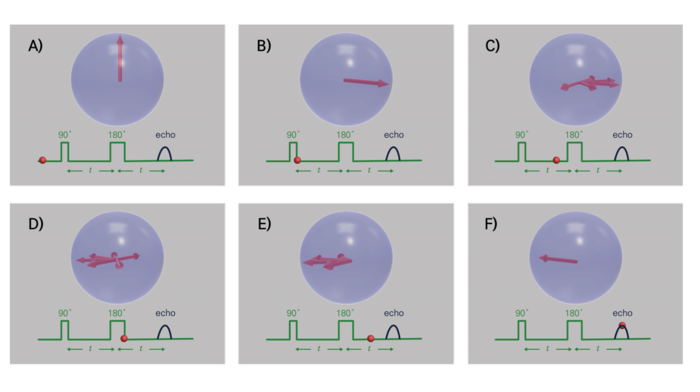
핵의 스핀 자기 공명에서 처음 개발된 기술로, 사용하는 전자기파 펄스를 적당한 시간 간격을 두고 2번 조사하면 이 시간 간격 후에 강한 신호가 관측된다. 이 신호가 메아리(echo)처럼 응답하므로 스핀 메아리(Spin echo)라고 한다. 이는 핵 스핀에서만 적용되지 않고, 전자 스핀계, 포톤, 포논 등에 대해서도 작용하는 것이 관측되었다. 양자정보과학에 널리 사용하는 기술로서 큐비트의 상태를 회복하는데 사용되고 있다.
스핀 메아리의 개수 및 다른 위상의 펄스를 연속적으로 적용하여 양자 상태의 결맞음 시간을 증가시키는 다양한 방법들이 고안되었다. 이를 동역학적 짝풀림(Dynamical decoupling) (DD)이라고 하며, Knill DD (KDD), CPMG(Carr-Purcell-Meiboom-Gill), Uhrig DD(UDD), periodic DD(PDD)등 다양한 펄스 적용 방법들이 있다.
AC 슈타르크 이동 (AC Stark Shift)[편집]
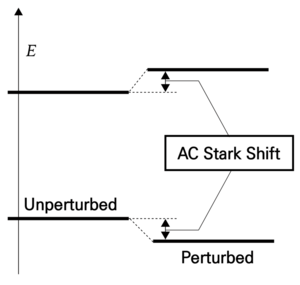
원자가 전자기장에 있을 경우 그 고유 에너지 상태가 전자기장에 의해 섭동하지 않을 경우에 비해 $$\pm \Omega^{2}/4\delta$$ 만큼 변하게 되는데 이를 a.c. Stark Shift라고 한다. Ω는 라비 진동으로 레이저의 세기를 의미하고, δ는 레이저와 원자의 에너지 레벨의 주파수 차이를 의미한다. 이는 광격자(Optical lattices)를 포함한 광 포획 기술의 원리가 된다. 또한 레이저 및 전자기장을 이용한 큐비트 조작 시 에너지 레벨을 변경시키는 원인이 되므로 공명 주파수를 사용할 때 충분히 고려해야 된다.
참고 문헌[편집]
- ↑ Rabi cycle, Wikipedia (https://en.wikipedia.org/wiki/Rabi_cycle)
- ↑ R. Wynands. and S. Weyers, Atomic fountain clocks, Metrologia 42(3), S64 (2005), doi:10.1088/0026-1394/42/3/S08.
- ↑ Spin echo, Wikipedia (https://en.wikipedia.org/wiki/Spin_echo)