양자 알고리듬 (Quantum Algorithm): 두 판 사이의 차이
Byeol Kang (토론 | 기여) |
|||
| (사용자 6명의 중간 판 63개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
= 계산 복잡도 (Computational Complexity) = | = 계산 복잡도 (Computational Complexity) = | ||
| 10번째 줄: | 5번째 줄: | ||
* 점근 표기법 (Asymptotic Notation) | * 점근 표기법 (Asymptotic Notation) | ||
알고리듬의 소요 시간이나 메모리 사용이 문제의 크기 $$n$$ 에 관한 함수 $$f(n)$$ 으로 정의 될때 $$n$$ 이 커짐에 함수의 증가를 다른 함수와의 점근적 대소관계로 표현하는 방법이다.<ref name=Cormen> | 알고리듬의 소요 시간이나 메모리 사용이 문제의 크기 $$n$$에 관한 함수 $$f(n)$$ 으로 정의 될때, $$n$$이 커짐에 함수의 증가를 다른 함수와의 점근적 대소관계로 표현하는 방법이다.<ref name=Cormen>T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein, ''Introduction to algorithms'' (MIT press, 2009).</ref> 큰(big) $$O$$ 표기법, 작은(small) $$o$$ 표기법, 큰(big) $$\Omega$$ 표기법, 작은(small) $$\omega$$ 표기법과 큰(big) $$\Theta$$ 표기법 등이 존재하며 일반적으로 복잡도의 상한을 정의하는 큰(big) $$O$$ 표기법이 가장 범용적으로 사용된다. | ||
* Big $$O$$ 표기법 | * 큰 (Big) $$O$$ 표기법 | ||
복잡도가 입력의 크기 $$n$$에 대해 $$f(n)$$이라는 관계를 가질 때, $$f(n) \in O(g(n))$$이라는 것은 다음을 의미한다. | 복잡도가 입력의 크기 $$n$$에 대해 $$f(n)$$이라는 관계를 가질 때, $$f(n) \in O(g(n))$$이라는 것은 다음을 의미한다. | ||
| 19번째 줄: | 14번째 줄: | ||
즉, 충분히 큰 $$n$$에 대해, $$g(n)$$의 상수배가 $$f(n)$$의 상한이라는 것을 의미한다. | 즉, 충분히 큰 $$n$$에 대해, $$g(n)$$의 상수배가 $$f(n)$$의 상한이라는 것을 의미한다. | ||
* Small $$o$$ 표기법 | * 작은 (Small) $$o$$ 표기법 | ||
큰 $$O$$와 유사하지만 $$f(n)$$ 이 $$g(n)$$ 보다 점근적으로 엄격하게 작다(strictly less)는 것을 의미한다. | |||
\[f(n) \in o | \[f(n) \in o(g(n)) \Leftrightarrow \lim_{n \rightarrow \infty}\frac{f(n)}{g(n)}= 0\] | ||
* Big $$\Omega$$ 표기법 | * 큰 (Big) $$\Omega$$ 표기법 | ||
큰 $$O$$와 반대로 $$f(n)$$이 $$g(n)$$ 보다 점근적으로 크다는 것을 의미한다. | |||
\[f(n) \in \Omega | \[f(n) \in \Omega(g(n)) \Leftrightarrow \lim_{n \rightarrow \infty}\left| \frac{f(n)}{g(n)} \right| > 0\] | ||
* Small $$\omega$$ 표기법 | * 작은 (Small) $$\omega$$ 표기법 | ||
작은 $$o$$ 와 마찬가지로 $$f(n)$$이 $$g(n)$$ 보다 엄격하게 크다(strictly large)는 것을 의미한다. | |||
\[f(n) \in \omega | \[f(n) \in \omega(g(n)) \Leftrightarrow \lim_{n \rightarrow \infty}\frac{f(n)}{g(n)}= \infty\] | ||
* Big $$\Theta$$ 표기법 | * 큰 (Big) $$\Theta$$ 표기법 | ||
$$f(n)$$이 $$O(g(n))$$이면서 $$\Omega(g(n))$$임을 의미한다. 즉 충분히 큰 $$n$$에 대하여, $$g(n)$$의 두 상수배가 $$f(n)$$의 상한과 하한이 되므로, $$f(n)$$과 $$g(n)$$이 점근적으로 같다는 것을 의미한다. | $$f(n)$$이 $$O(g(n))$$이면서 $$\Omega(g(n))$$임을 의미한다. 즉 충분히 큰 $$n$$에 대하여, $$g(n)$$의 두 상수배가 $$f(n)$$의 상한과 하한이 되므로, $$f(n)$$과 $$g(n)$$이 점근적으로 같다는 것을 의미한다. | ||
\[f(n) \in \Theta | \[f(n) \in \Theta(g(n)) \Leftrightarrow f(n) \in O(g(n)), f(n) \in \Omega(g(n))\] | ||
일반적으로 기호의 남용임에도 불구하고, | 일반적으로 기호의 남용임에도 불구하고, | ||
\[f(n) \in O | \[f(n) \in O(g(n))\] | ||
인 경우, | 인 경우, | ||
\[f(n)= O | \[f(n)= O(g(n))\] | ||
\ | 이라고 표기한다. 예를 들어 $$f(n)= an^{2} + bn + c $$일때, $$f(n)= O(n^{2})$$이라 할 수 있는데, 왜냐하면 $$\lim\limits_{n \rightarrow \infty}\frac{f(n)}{n^{2}}= a < \infty$$이기 때문이다. | ||
어떤 알고리듬의 시간 복잡도 $$f(n)$$이 $$O | 어떤 알고리듬의 시간 복잡도 $$f(n)$$이 $$O(n^{a})$$ 인 경우 해당 알고리듬은 다룰 수 있는(tractable) 알고리듬으로 분류되고 $$f(n)$$이 $$O(a^{n})$$인 경우에는 다루기 힘든(intractable) 알고리듬으로 분류된다. 다루기 힘든 알고리듬의 경우 $$n$$이 커짐에 따라 소요 시간이 지수적으로 증가하므로 실질적인 의미에서 풀 수 없다고 볼 수 있다. | ||
* P 문제 | * P 문제 | ||
다항시간의 | 다항시간의 시간 복잡도를 가진 알고리듬이 발견된 문제들이다. 고전 컴퓨터로 효율적으로 풀 수 있다. 조금 더 정확히 말하면, 다항시간 내에 결정론적으로(deterministically) 풀 수 있는 결정문제(decision problem)이다. 결정문제란 예, 아니오의 형태로 답하는 문제인데, 많은 문제들이 다항시간 안에 결정문제로 변환될 수 있기 때문에 문제 분석에 활용된다. | ||
* NP 문제 | * NP 문제 | ||
답이 주어졌을 때 다항시간의 복잡도로 답을 검증할 수 있는 문제이다. 또는 다항시간 내에 비결정론적( | 답이 주어졌을 때 다항시간의 복잡도로 답을 검증할 수 있는 문제이다. 또는 다항시간 내에 비결정론적(non-deterministically)으로 풀 수 있는 결정문제(non-deterministic polynomial time class)이다. 비결정론적이라는 것은 같은 문제에 대해 알고리듬을 실행할 때 얻는 결과가 달라질 수 있음을 의미한다. 즉, NP 문제는 항상은 아니지만 다항시간 내에 풀 때도 있다는 것이다. P 문제는 다항시간 안에 결정론적으로 해를 구할 수 있으므로 자명하게 NP 문제에 포함되며 P문제에 속하는 것이 증명이 되지 않은 경우 암호화 등에 사용된다. [[양자 컴퓨터]]는 소인수분해나 이산 로그(discrete logarithm)와 같은 NP 문제를 다항시간내에 풀 수 있기 때문에 기존에 사용되는 암호화 알고리듬을 무력화할 가능성이 크다. 양자 알고리듬의 고전 컴퓨터 알고리듬에 대한 우위는 동일한 알고리듬이 양자 컴퓨터에서 더 나은 수행시간으로 실행가능한지로부터 말할 수 있는 것이 아니라, 동일한 문제가 양자 컴퓨터에서 더 나은 시간 복잡도를 가질 수 있다는 사실로부터 나온다고 할 수 있다. | ||
= 양자 푸리에 변환 (Quantum Fourier Transform) = | = 양자 푸리에 변환 (Quantum Fourier Transform) = | ||
양자 푸리에 변환은 이산 푸리에 변환( | 양자 푸리에 변환은 이산 푸리에 변환(discrete Fourier transform) | ||
\[y_{k} = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1}x_j e^{\frac{2 \pi ijk}{N}}\] | \[y_{k} = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1}x_j e^{\frac{2 \pi ijk}{N}}\] | ||
| 69번째 줄: | 60번째 줄: | ||
을 [[양자 컴퓨터]]를 통해 수행하는 알고리즘이다. | 을 [[양자 컴퓨터]]를 통해 수행하는 알고리즘이다. | ||
일반적으로 이산 푸리에 변환이 길이가 $$N(= 2^{n})$$인 배열( | 일반적으로 이산 푸리에 변환이 길이가 $$N(= 2^{n})$$인 배열(array)에 대해 정의되는 것에 비해 양자 푸리에 변환은 직교 기저(orthonormal basis) $$\left| \left. 0 \right\rangle \right. $$, …, $$\left| \left. N - 1 \right\rangle \right. $$에 대해 다음과 같이 정의된다. | ||
\[\left. |j \right\rangle \overset{\text{QFT}}{\rightarrow}\frac{1}{\sqrt{N}}\sum_{k= 0}^{N - 1}{e^{\frac{2\pi ijk}{N}}\left. |k \right\rangle} | \[\begin{align*} | ||
\left. |j \right\rangle \overset{\text{QFT}}{\rightarrow}\frac{1}{\sqrt{N}}\sum_{k= 0}^{N - 1}{e^{\frac{2\pi ijk}{N}}\left. |k \right\rangle} | |||
&= \frac{1}{\sqrt{N}} \sum_{k_{1} =0}^{1}\ldots\sum_{k_{n}= 0}^{1}{e^{2\pi ij(\sum_{l =1}^{n}{k_{l}2^{- l}})}\left. |k_{1}\ldots k_{n} \right\rangle} \\ | |||
&= \frac{1}{\sqrt{N}} \sum_{k_{1} =0}^{1}\ldots\sum_{k_{n}= 0}^{1}{\otimes_{l =1}^{n}e^{2\pi ijk_{l}2^{- l}}\left. |k_{l} \right\rangle} \\ | |||
&= \frac{1}{\sqrt{N}} \otimes_{l =1}^{n}\left\lbrack \sum_{k_{l}= 0}^{1}{e^{2\pi ijk_{l}2^{- l}}\left. |k_{l} \right\rangle} \right\rbrack \\ | |||
&= \frac{1}{\sqrt{N}} \otimes_{l =1}^{n}\left\lbrack \left. |0 \right\rangle + e^{2\pi ijk_{l}2^{- l}}\left. |1 \right\rangle \right\rbrack \\ | |||
&= \frac{\left( \left. |0 \right\rangle + e^{2\pi ij0.j_{n}}\left. |1 \right\rangle \right)\ldots\left( \left. |0 \right\rangle + e^{2\pi ij0.{j_{1}\ldots j}_{n}}\left. |1 \right\rangle \right)}{\sqrt{N}} \\ | |||
\end{align*}\] | |||
알고리듬의 | 알고리듬의 시간 복잡도는 $$O( \left( \log N \right)^{2})$$으로 (또는 $$O(n^{2})$$) 고전 컴퓨터에서 고속 푸리에 변환의 시간 복잡도 $$O(N\log{N)}$$에 비해 지수적으로 빠르게 수행된다. | ||
* 구현 | * 구현 | ||
<blockquote>하다마드 게이트(Hadamard gate)와 조건부 위상 게이트(controlled phase gate)로 구성된다 | <blockquote>하다마드 게이트(Hadamard gate)와 조건부 위상 게이트(controlled phase gate)로 구성된다. 게이트에 대한 보다 상세한 내용은 [[양자 게이트]]를 참고하라.</blockquote> | ||
* 하다마드 게이트 (Hadamard Gate) | * 하다마드 게이트 (Hadamard Gate) | ||
| 94번째 줄: | 87번째 줄: | ||
* 조건부 위상 게이트 (Controlled Phase Gate) | * 조건부 위상 게이트 (Controlled Phase Gate) | ||
조건부 [[큐비트]]의 값에 따라 항등 게이트(identity | 조건부 [[큐비트]]의 값에 따라 항등 게이트(identity gate)로 작용하거나 특정 각도의 회전으로 작용한다. 특정 각도 회전 게이트는 계산 기저에 대해 다음과 같이 표현된다. | ||
\[R_{m}= \begin{pmatrix} | \[R_{m}= \begin{pmatrix} | ||
1 & 0 \\ | 1 & 0 \\ | ||
0 & e^{\frac{2\ | 0 & e^{\frac{2\pi i}{2^{m}}}\\ | ||
\end{pmatrix}\] | \end{pmatrix}\] | ||
각 [[큐비트]]가 알고리듬이 요구하는 상태가 되기 위해서는 $$i$$번째 [[큐비트]]가 $$n - i + 1$$개의 [[게이트]]를 필요로 하기 때문에 전체 필요한 [[게이트]]의 수는 | 각 [[큐비트]]가 알고리듬이 요구하는 상태가 되기 위해서는 $$i$$번째 [[큐비트]]가 $$n - i + 1$$개의 [[게이트]]를 필요로 하기 때문에 전체 필요한 [[게이트]]의 수는 다음과 같다. | ||
\[\sum_{i= 1}^{n}{(n - i + 1)} =\frac{n(n + 1)}{2}\] | \[\sum_{i= 1}^{n}{(n - i + 1)} =\frac{n(n + 1)}{2}\] | ||
즉, [[게이트]]의 수는 [[큐비트]] | 즉, [[게이트]]의 수는 [[큐비트]] 개수의 제곱에 비례하게 증가하며 [[큐비트]]의 개수는 입력 크기의 로그에 비례하여 증가한다. 따라서 시간 복잡도는 $$O( \left( \log N \right)^{2} )$$ 이며 공간 복잡도는 추가적인 큐비트를 필요로 하지 않기 때문에 $$O(\log N)$$이다. | ||
[[File: | [[File:기술백서_전체수정_6차_4_resize.jpg|none|thumb|500px|양자 푸리에 변환 회로.<ref>https://en.wikipedia.org/wiki/Quantum_Fourier_transform</ref> 참고문헌 [2]의 그림을 재구성함. | ||
]] | ]] | ||
= 양자 위상 추정 (Quantum Phase Estimation) = | = 양자 위상 추정 (Quantum Phase Estimation) = | ||
[[양자 푸리에 변환]]을 이용하여 특정 | [[양자 푸리에 변환]]을 이용하여 특정 유니타리(unitary) 연산자 $$U$$의 고윳값(eigenvalue) $$e^{2\pi i\varphi}$$ 을 추정하는 알고리듬을 양자 위상 추정이라고 한다. 고윳값에 해당하는 고유벡터(eigenvector) $$\left| \left. u \right\rangle \right. $$와 controlled-$$U^{2^{j}}$$ [[게이트]]가 주어졌다고 가정하자. 양자 위상 추정 알고리듬은 위상 추정을 위한 $$t$$개의 [[큐비트]]와 $$\left| \left. u \right\rangle \right. $$를 표현하기 위해 필요한 [[큐비트]]를 사용한다. | ||
* 구현 | * 구현 | ||
$$t$$개의 [[큐비트]]를 $$\left| \left. 0 \right\rangle \right. $$으로 초기화한 후 하다마드 [[게이트]]를 적용한다. 이후 $$t$$개의 [[큐비트]]를 컨트롤로 하여 | $$t$$개의 [[큐비트]]를 $$\left| \left. 0 \right\rangle \right. $$으로 초기화한 후 하다마드 [[게이트]]를 적용한다. 이후 $$t$$개의 [[큐비트]]를 컨트롤로 하여 $$t$$개의 controlled-$$U^{2^{j}}$$ 게이트를 아래 그림에서와 같이 적절히 수행하면 출력은 다음과 같은 형태가 된다. | ||
\[\frac{1}{2^{\frac{t}{2}}}\left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{t - 1}\varphi}\left| \left. 1 \right\rangle \right. \right)\left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{t - 2}\varphi}\left| \left. 1 \right\rangle \right. \right)\ldots\left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{0}\varphi}\left| \left. 1 \right\rangle \right. ) = \frac{1}{2^{\frac{t}{2}}}\sum_{k =0}^{2^{t} - 1}{e^{2\pi i\varphi k}\left| \left. k \right\rangle \right. }\] | \[\frac{1}{2^{\frac{t}{2}}}\left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{t - 1}\varphi}\left| \left. 1 \right\rangle \right. \right)\left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{t - 2}\varphi}\left| \left. 1 \right\rangle \right. \right)\ldots \left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{0}\varphi}\left| \left. 1 \right\rangle \right. \right) = \frac{1}{2^{\frac{t}{2}}}\sum_{k =0}^{2^{t} - 1}{e^{2\pi i\varphi k}\left| \left. k \right\rangle \right. }\] | ||
해당 출력에 역 양자 푸리에 변환(inverse QFT)을 적용할 때 출력은 다음과 같다. | 해당 출력에 역 양자 푸리에 변환(inverse QFT)을 적용할 때 출력은 다음과 같다. | ||
| 123번째 줄: | 116번째 줄: | ||
\[\frac{1}{2^{\frac{t}{2}}}\sum_{k= 0}^{2^{t} - 1}{e^{2\pi i\varphi k}\left| \left. k \right\rangle \right. } \rightarrow \left| \left. \widetilde{\varphi} \right\rangle \right. \] | \[\frac{1}{2^{\frac{t}{2}}}\sum_{k= 0}^{2^{t} - 1}{e^{2\pi i\varphi k}\left| \left. k \right\rangle \right. } \rightarrow \left| \left. \widetilde{\varphi} \right\rangle \right. \] | ||
여기에서 $$\widetilde{\varphi}$$는 $$\varphi$$의 t-비트 근사값이 된다. 따라서 $$t$$개의 [[큐비트]]를 측정하면 | 여기에서 $$\widetilde{\varphi}$$는 $$\varphi$$의 $$t$$-비트 근사값이 된다. 따라서 $$t$$개의 [[큐비트]]를 측정하면 고윳값 $$\varphi$$의 근사값을 얻는다. | ||
[[File: | [[File:기술백서_전체수정_6차_5_resize.jpg|none|thumb|500px|양자 위상 추정 알고리듬 회로도.<ref>https://en.wikipedia.org/wiki/Quantum_phase_estimation_algorithm</ref> $$U= U_a$$ 이고, $$|\psi> = |1>$$ 인 양자 위상 추정 알고리듬의 회로도. 참고문헌 [3]의 그림을 재구성함. | ||
]] | |||
각각의 controlled-$$U^{2^{j}}$$ 게이트가 상수시간으로 실행됨을 가정하면 시간 복잡도는 [[양자 푸리에 변환]]과 동일하게 $$O | 각각의 controlled-$$U^{2^{j}}$$ 게이트가 상수시간으로 실행됨을 가정하면 시간 복잡도는 [[양자 푸리에 변환]]과 동일하게 $$O(t^{2})$$이 된다. $$U$$게이트의 고윳값이 $$t$$개의 [[큐비트]]로 나타낼 수 없는 경우에는 추정에 사용하는 [[큐비트]]의 개수를 늘림으로써 정확도를 상승시킬 수 있다. | ||
만약 $$1 - \ | 만약 $$1 - \varepsilon$$의 확률로 $$2^{- n}$$의 정밀도로 올바른 추정값을 얻기 위해서는 | ||
\[t= n + \left\lceil \log\left( 2 + \frac{1}{2\ | \[t= n + \left\lceil \log\left( 2 + \frac{1}{2\varepsilon} \right) \right\rceil\] | ||
개의 [[큐비트]]가 필요하다.<ref name=Nielsen> | 개의 [[큐비트]]가 필요하다.<ref name=Nielsen>M. A. Nielsen and I. L. Chuang, ''Quantum computation and quantum information'' (Cambridge University Press, 2002)</ref> | ||
= 쇼어 알고리듬 (Shor’s Algorithm) = | = 쇼어 알고리듬 (Shor’s Algorithm) = | ||
$$n$$비트로 표현되는 자연수를 | $$n$$비트로 표현되는 자연수를 고전 컴퓨터로 소인수분해하는 알고리듬은 $$O(\text{exp}\left( n^{\frac{1}{3}}\log^{\frac{2}{3}}n \right))$$ 의 시간 복잡도를 가진다. 이러한 계산 복잡도는 지수적이므로 큰 수를 소인수분해하는 것은 다루기 힘든(intractable) 문제로 여겨지며 이는 현재 가장 대중적으로 사용되는 공개키 알고리듬인 RSA 알고리듬의 기반이 된다. 그러나 쇼어 알고리듬은 [[양자 푸리에 변환]]을 이용하여 $$O(n^{2}\log{n\log{\log{n)}}}$$의 시간 복잡도로 $$n$$비트 자연수의 소인수분해를 수행할 수 있다. 이는 다항시간이므로 현재 사용되는 암호화를 손쉽게 무력화할 수 있을 것으로 예상되며 이는 양자 컴퓨터의 킬러 애플리케이션이 될 것으로 예상된다. | ||
* 차수 찾기 알고리듬 ( | * 차수 찾기 알고리듬 (Order Finding Algorithm) | ||
어떤 수 $$x$$의 모듈로 $$N$$에 관한 차수(order of $$x$$ modulo $$N$$)는 | 어떤 수 $$x$$의 모듈로 $$N$$에 관한 차수(order of $$x$$ modulo $$N$$)는 | ||
\[x^{r} \equiv 1 \left( \text{mod}\ | \[x^{r} \equiv 1 \left( \text{mod}\,N \right)\] | ||
을 만족하는 가장 작은 자연수 $$r$$로 정의된다. | 을 만족하는 가장 작은 자연수 $$r$$로 정의된다. | ||
양자 위상 추정 알고리듬을 사용하면 $$O(\left( \log N \right)^{3})$$의 시간 복잡도로 계산할 수 있다.<ref name=Nielsen | 양자 위상 추정 알고리듬을 사용하면 $$O(\left( \log N \right)^{3})$$의 시간 복잡도로 계산할 수 있다.<ref name=Nielsen /> 쇼어 알고리듬은 차수 찾기 알고리듬을 통해 효율적으로 소인수의 후보를 탐색하는 방식으로 작동한다. | ||
* 구현 | * 구현 | ||
$$\left| \left. j \right\rangle \right. \left| \left. k \right\rangle \right. \rightarrow \left| \left. j \right\rangle \right. \left| \left. x^{j}\ | $$\left| \left. j \right\rangle \right. \left| \left. k \right\rangle \right. \rightarrow \left| \left. j \right\rangle \right. \left| \left. x^{j} k\, \text{mod}\, N \right\rangle \right. $$ 으로 변환하는 블랙박스 $$U_{x}$$가 구현되어 있다고 가정하자. $$t= 2L + 1 + \left\lceil \log(2 + 1/2\varepsilon) \right\rceil $$개의 양자 위상 추정을 위한 큐비트를 사용하면 $$O(L^{3}{) }$$의 시간 복잡도로 차수를 계산할 수 있다. 여기서 $$L{ =\left\lceil \log N \right\rceil\text{ }}$$이라고 한다. 쇼어 알고리듬은 $$x$$를 랜덤하게 선택하여 $$N$$의 소인수분해를 시도한다. 만약 $$x^{r} \equiv 1 \left( \text{mod}\,N \right)$$ 일 때, $$r$$이 짝수인 경우 $$\left( x^{\frac{r}{2}} - 1 \right)\left( x^{\frac{r}{2}} + 1 \right) \equiv 0 \left( \text{mod}\,N \right)$$ 이므로 $$\text{gcd}(\left( x^{\frac{r}{2}} - 1 \right), N)$$과 $$\text{gcd}(\left( x^{\frac{r}{2}} + 1 \right), N)$$을 계산하여 1이 아닌 최대공약수를 갖는다면 해당 자연수로 $$N$$을 인수분해한다. $$r$$이 홀수인 경우 다른 $$x$$를 선택한다. | ||
이러한 과정을 반복하면 다항시간으로 $$N$$을 소인수분해할 수 있음이 알려져 있다.<ref name=Nielsen | 이러한 과정을 반복하면 다항시간으로 $$N$$을 소인수분해할 수 있음이 알려져 있다.<ref name=Nielsen /> 간단하게 동작 원리를 알아 보면, 먼저 양자 위상 추정을 사용하기 위해 $$U_{a}$$의 고윳값과 고유벡터가 어떻게 되는지를 살펴봐야 한다. 그러면 $$s \in \{ 0,1,\ldots,r - 1\}$$ 에 대하여 고유벡터와 고윳값은 각각 $$\left| \left. u_{s} \right\rangle \right.= \frac{1}{\sqrt{r}}\sum_{j =0}^{r - 1}e^{- \frac{2\pi isj}{r}}\left| \left. a^{j}\,\text{mod}\,N \right\rangle \right. $$과 $$e^{\frac{2\pi is}{r}}$$이 됨을 알 수 있다. 이 때 모든 고유벡터를 [[중첩]]시키면 $$\frac{1}{\sqrt{r}}\sum_{s= 0}^{r - 1}\left| \left. u_{s} \right\rangle \right. =\left| \left. 1 \right\rangle \right. $$이 된다. 그렇기 때문에 아래 그림에서 양자 위상 추정을 위한 고유벡터로 $$\left| \left. 1 \right\rangle \right. $$을 사용한 것이다. 이렇게 하면 양자 위상 추정을 통해 $$s/r$$를 추정할 수 있고, 이를 통해 $$r$$ 값을 추정하여 위에서 언급한 방법대로 인수분해가 가능한지 검사한다. | ||
현재 큰 수의 소인수분해가 어렵다는 것은 | 현재 큰 수의 소인수분해가 어렵다는 것은 RSA 암호를 비롯한 공개키 암호의 근간을 이루므로 해당 알고리듬은 현재 발견된 양자 알고리듬 중 가장 유용한 킬러 애플리케이션으로 여겨진다. | ||
[[File: | [[File:기술백서_전체수정_6차_6_resize.jpg|none|thumb|500px|쇼어 알고리듬의 회로도.<ref>https://en.wikipedia.org/wiki/Shor%27s_algorithm</ref> 참고문헌 [5]의 그림을 재구성함. | ||
]] | ]] | ||
= 그로버 알고리듬 (Grover’s Algorithm) = | = 그로버 알고리듬 (Grover’s Algorithm) = | ||
그로버 알고리듬은 앞서 소개한 양자 푸리에 변환 기반 알고리듬과 함께 현재 알려진 양자 알고리듬의 두 가지 축 중 하나이다. $$N$$개의 원소에 대해 정의된 함수 $$f(x)= 1$$의 | 그로버 알고리듬은 앞서 소개한 양자 푸리에 변환 기반 알고리듬과 함께 현재 알려진 양자 알고리듬의 두 가지 축 중 하나이다. $$N$$개의 원소에 대해 정의된 함수 $$f(x)= 1$$의 해인 $$M$$개의 $$x$$를 찾는 알고리즘이며, 앞서 소개된 알고리듬과 달리 지수적인 속도 상승을 보여주지는 못하지만 고전적 알고리듬보다 제곱근의 시간 복잡도를 갖는다. | ||
* 구현 | * 구현 | ||
입력 $$\left| \left. x \right\rangle \right. \left| \left. q \right\rangle \right. $$ 에 대하여 출력 $$\left| \left. x \right\rangle \right. \left| \left. f(x) \oplus q \right\rangle \right. $$ 를 내보내는 오라클(oracle) $$O$$ 가 존재한다고 가정하자. | 입력 $$\left| \left. x \right\rangle \right. \left| \left. q \right\rangle \right. $$ 에 대하여 출력 $$\left| \left. x \right\rangle \right. \left| \left. f(x) \oplus q \right\rangle \right. $$ 를 내보내는 오라클(oracle) $$O$$ 가 존재한다고 가정하자. | ||
# 하다마드 [[게이트]]를 사용하여 $$\left| \left. 0 \right\rangle \right. ^{\otimes n}$$을 $${\frac{1}{\sqrt{2^{n}}}\left( \left. \left| 0 \right. \right\rangle + \left. \left| 1 \right. \right\rangle \right)}^{\otimes n}$$으로 변환, | # 하다마드 [[게이트]]를 사용하여 $$\left| \left. 0 \right\rangle \right. ^{\otimes n}$$을 $${\frac{1}{\sqrt{2^{n}}}\left( \left. \left| 0 \right. \right\rangle + \left. \left| 1 \right. \right\rangle \right)}^{\otimes n}$$으로 변환, 보조 큐비트 $$\left| \left. q \right\rangle \right. $$는 $$\left| \left. 1 \right\rangle \right. $$에 하다마드 게이트를 사용하여 $$\frac{1}{\sqrt{2}}\left( \left. \left| 0 \right. \right\rangle - \left. \left| 1 \right. \right\rangle \right)$$로 변환 | ||
# 오라클 $$O$$를 적용 | # 오라클 $$O$$를 적용 | ||
# $$\left| \left. x \right\rangle \right. $$에 대하여 하다마드 게이트를 적용 | # $$\left| \left. x \right\rangle \right. $$에 대하여 하다마드 게이트를 적용 | ||
# 조건부 위상 | # 조건부 위상 변조(conditional phase shift)를 적용하여 $$\left| \left. x \right\rangle \right. \rightarrow - ( - 1)^{\delta _{x0}}\left| \left. x \right\rangle \right. $$ 로 변환(여기에서 $$\delta$$는 크로네커 델타) | ||
# $$\left| \left. x \right\rangle \right. $$에 대하여 하다마드 게이트를 적용 | # $$\left| \left. x \right\rangle \right. $$에 대하여 하다마드 게이트를 적용 | ||
# 2)~5) 를 반복 적용한 후 측정하여 $$f(x)= 1$$인 $$x$$를 얻음 | # 2)~5) 를 반복 적용한 후 측정하여 $$f(x)= 1$$인 $$x$$를 얻음 | ||
| 174번째 줄: | 168번째 줄: | ||
3)~5) 과정은 ‘평균에 대한 반전(inversion about average)’ 이라고 불리며, 모든 계산기저의 평균이라고 할 수 있는 1) 단계 이후의 상태에 대해 뒤집는 변환을 말한다. 해당 상태는 하다마드 게이트에 의해 $$\left| \left. 0 \right\rangle \right. ^{\otimes n}$$으로 변환되므로 4) 단계의 앞뒤로 하다마드 게이트를 적용하여 평균에 대한 반전을 구현할 수 있다. 이러한 과정은 찾고자 하는 해가 측정될 확률을 증폭시켜줄 수 있는데, 2) 단계에서 오라클에 의해 $$f(x)= 1$$인 $$\left| \left. x \right\rangle \right. $$들의 위상이 뒤집히기 때문이다. 그러나 일정 횟수 이상 실행하면 오히려 확률을 떨어뜨리기 때문에, 매번 증폭시키지는 않는다. | 3)~5) 과정은 ‘평균에 대한 반전(inversion about average)’ 이라고 불리며, 모든 계산기저의 평균이라고 할 수 있는 1) 단계 이후의 상태에 대해 뒤집는 변환을 말한다. 해당 상태는 하다마드 게이트에 의해 $$\left| \left. 0 \right\rangle \right. ^{\otimes n}$$으로 변환되므로 4) 단계의 앞뒤로 하다마드 게이트를 적용하여 평균에 대한 반전을 구현할 수 있다. 이러한 과정은 찾고자 하는 해가 측정될 확률을 증폭시켜줄 수 있는데, 2) 단계에서 오라클에 의해 $$f(x)= 1$$인 $$\left| \left. x \right\rangle \right. $$들의 위상이 뒤집히기 때문이다. 그러나 일정 횟수 이상 실행하면 오히려 확률을 떨어뜨리기 때문에, 매번 증폭시키지는 않는다. | ||
2)~5) 과정은 solution | 2)~5) 과정은 해 공간(solution space)에서 $$\theta$$ 회전에 해당하며, | ||
\[\sin\theta= \frac{2\sqrt{M(N - M) }}{N}\] | \[\sin\theta= \frac{2\sqrt{M(N - M) }}{N}\] | ||
| 180번째 줄: | 174번째 줄: | ||
$$M \ll N$$이면, | $$M \ll N$$이면, | ||
\[\theta \approx sin\theta \approx 2\sqrt{\frac{M}{N}}\] | \[\theta \approx \sin\theta \approx 2\sqrt{\frac{M}{N}}\] | ||
최대 $$\frac{\pi}{2} $$의 회전이 필요하므로 | 최대 $$\frac{\pi}{2} $$의 회전이 필요하므로 $$\theta$$ 회전의 개수는, | ||
\[R \leq \left\lceil \frac{\pi}{4}\sqrt{\frac{N}{M}} \right\rceil\] | \[R \leq \left\lceil \frac{\pi}{4}\sqrt{\frac{N}{M}} \right\rceil\] | ||
이다. 따라서 시간 복잡도는 $$O | 이다. 따라서 시간 복잡도는 $$O(\sqrt{N/M})$$ 이며 이는 고전 컴퓨터 알고리듬의 시간 복잡도 $$O(\frac{N}{M})$$ 에 비해 제곱근만큼 빠르게 작동한다. 이는 그로버 알고리듬이 $$N$$개의 입력을 동시에 처리함을 보여준다. 그러나 이를 위해서는 적절한 오라클을 구현하는 것이 중요하다. | ||
[[File: | [[File:기술백서_전체수정_6차_7_resize.jpg|none|thumb|500px|그로버 알고리듬의 회로도.<ref>https://en.wikipedia.org/wiki/Grover%27s_algorithm</ref> 참고문헌 [6]의 그림을 재구성함. | ||
]] | ]] | ||
= 양자 기계 학습 (Quantum Machine Learning) = | = 양자 기계 학습 (Quantum Machine Learning) = | ||
양자 이점을 | 양자 이점을 기계 학습에 적용하려는 노력은 최근 부상하고 있으나 현재 기반이 되는 하드웨어의 부재로 인해 이론적인 연구로서만 존재하고 있다. 어떠한 알고리듬이 실제로 구현 가능할 것인지는 아직 명확하지 않으며 본문에서는 제안된 몇 가지 알고리듬을 소개하고자 한다. | ||
* 양자 진폭 시뮬레이션 (Quantum Amplitude Simulation) | * 양자 진폭 시뮬레이션 (Quantum Amplitude Simulation) | ||
고전 컴퓨터에 작동하는 | 고전 컴퓨터에 작동하는 기계 학습 알고리듬을 양자 컴퓨터로 효율적으로 시뮬레이션하면서 이점을 얻으려는 시도로서 대표적으로 행렬계산을 효율적으로 수행함을 목표로 한다. $$n$$개의 큐비트는 $$2^{n}$$개의 상태를 저장할 수 있기 때문에 [[큐비트]] 개수에 대해 다항시간의 시간 복잡도를 가진 알고리듬을 사용하여 기계 학습에 사용되는 계산을 수행할 수 있다면 지수적인 시간 복잡도 상승을 얻을 수 있다. 예를 들어 HHL 알고리듬은 특정 조건을 만족하는 행렬의 역행렬 계산을 행렬의 차원의 로그에 해당하는 복잡도로 수행할 수 있다.<ref name=Harrow>A. Harrow, Quantum algorithm for solving linear systems of equations, in ''Proceedings of APS March Meeting 2010 '' '''55''', 2 (2010).</ref> 이는 고전 컴퓨터 알고리듬의 $$O(n^{2})$$의 복잡도에 비해 지수적인 속도상승을 보여준다. 현재 시뮬레이션 수행의 가장 큰 난관은 데이터를 양자 상태로 변환하는 것으로 아직 일반적인 데이터를 변환할 때 $$O( n^{2})$$ 이상의 시간 복잡도가 필요하므로 실제적인 이점을 얻기 위해서는 해당 부분에서 새로운 알고리듬이 고안되어야 할 것이다. | ||
* 그로버 알고리듬 기반 기계 학습 | |||
그로버 알고리듬은 $$N$$개의 원소 중 조건을 만족하는 원소를 고전 알고리듬에 비해 제곱배로 빠르게 찾아낼 수 있으므로 $$k$$-median 이나 $$k$$-nearest neighbor 와 같은 문제를 방대한 데이터셋에서 빠르게 찾아낼 수 있을 것으로 기대된다.<ref name=Aïmeur>E. Aïmeur, G. Brassard, and S. Gambs, Quantum speed-up for unsupervised learning, Machine Learning '''90''', 261 (2013). doi:[https://doi.org/10.1007/s10994-012-5316-5 10.1007/s10994-012-5316-5].</ref><ref name=Wiebe>N. Wiebe, A. Kapoor, and K. Svore, Quantum algorithms for nearest-neighbor methods for supervised and unsupervised learning, arXiv:[https://arxiv.org/abs/1401.2142 1401.2142].</ref> | |||
* 양자 신경망 (Quantum Neural Network) | * 양자 신경망 (Quantum Neural Network) | ||
고전 신경망을 양자 컴퓨터로 구현하여 양자역학적 효과를 학습 알고리듬으로 사용하는 것을 목적으로 한다. 퍼셉트론(perceptron)을 양자 컴퓨터로 구현하기위해 입출력간 비선형성을 가진 회로를 구현하는 연구가 활발히 진행중이다.<ref name=Gupta>S. Gupta and R. K. P. Zia, Quantum neural networks, Journal of Computer and System Sciences '''63''', 355 (2001). doi:[https://doi.org/10.1006/jcss.2001.1769 10.1006/jcss.2001.1769].</ref> | |||
다른 접근방식으로 [[그로버 알고리듬]] 기반으로 연관 메모리(associative memory)를 구현하려는 시도가 있다.<ref name=Ventura> | 다른 접근방식으로 [[그로버 알고리듬]] 기반으로 연관 메모리(associative memory)를 구현하려는 시도가 있다.<ref name=Ventura>D. Ventura and T. Martinez, Quantum associative memory, Information Sciences '''124''', 273 (2000). doi:[https://doi.org/10.1016/S0020-0255(99)00101-2 10.1016/S0020-0255(99)00101-2].</ref> 즉 입력과 가장 비슷한 메모리를 그로버 알고리듬을 통해 찾아내는 방식으로 작동한다. 이러한 방식은 메모리의 크기가 [[큐비트]]의 개수에 지수적으로 증가하므로 효율적인 저장이 가능하다는 이점을 가지고 있다. 그러나 이 모델의 유용성은 이러한 단순화된 연관 메모리가 실질적인 효용을 가진다는 것을 실증하는데에 있으며 이는 실제 [[양자 컴퓨터]]나 그러한 [[양자 컴퓨터]]를 시뮬레이션 할 수 있는 고전 컴퓨터를 통해서만 입증될 것이다. | ||
= 최신 성능 개괄 = | = 최신 성능 개괄 = | ||
== 양자 알고리듬== | == 양자 알고리듬 (Quantum Algorithm)== | ||
양자 알고리듬은 [[쇼어 알고리듬|쇼어 알고리듬(Shor’s | 양자 알고리듬은 [[쇼어 알고리듬|쇼어 알고리듬(Shor’s algorithm)]]이 나타나면서 각광받기 시작했다. [[쇼어 알고리듬]]은 [[양자 푸리에 변환|양자 푸리에 변환(quantum fourier transform)]]을 기반으로, 소인수분해나 이산대수문제를 기존 컴퓨터보다 기하급수적으로 빠른 속도로 연산이 가능하다. 그리고 현재 사용되는 [[양자 암호 통신|암호화 알고리듬]]은 RSA 알고리듬(Rivest-Shamir-Adleman algorithm)으로, 큰 정수의 소인수분해가 기존 컴퓨터로는 어렵다는 점에 착안해서 만들어진 방식이다. 이로 인해 양자 컴퓨터에 대비해서 암호화 분야에는 비상이 걸리고, 양자 컴퓨터는 각광을 받기 시작한다. 양자 컴퓨터의 성능이 좋아지면 기존 암호화 방식인 RSA 알고리듬이 무력화될 가능성이 있지만, 아직은 양자 컴퓨터는 많은 수의 큐비트 구현이 불가능해서 기존 암호화 방식을 위협하기엔 시간이 걸린다. | ||
많이 알려진 양자 알고리듬 중에서 | 많이 알려진 양자 알고리듬 중에서 번스타인-바지라니 알고리듬(Bernstein-Vazirani algorithm)도 있다. 이는 임의의 수를 정하고, 이 수를 맞추는 알고리듬으로 기존 방식으로 연산하는 것보다 연산 단계가 적다. 예를 들어 4 비트의 길이를 갖는 숨겨진 임의의 수를 1001이라고 하자. 기존 알고리듬은 먼저 임의의 수와 0001을 비교한다. AND(1, 1)은 1이므로 첫번째 수가 1이라는 것을 알 수 있다. 다음으로 0010와 비교하며 각 비트를 비교한 후에 임의의 수를 알아낼 수 있다. 총 비교 수는 비트 수만큼 반복한다. 하지만 번스타인-바지라니 알고리듬은 [[큐비트]]의 수에 상관없이 단 한번의 연산으로 임의의 수를 알아낼 수 있다. 실용성 외에도, 이러한 알고리듬은 양자 우월성을 입증하고 양자 컴퓨터의 기하 급수적인 속도 향상을 증명하기도 한다. | ||
현재는 | 현재는 양자 컴퓨터의 성능을 비교, 판단할 때 [[쇼어 알고리듬|쇼어 알고리듬(Shor’s algorithm)]], 번스타인-바지라니 알고리듬(Bernstein-Vazirani algorithm), [[그로버 알고리듬|그로버 알고리듬(Grover’s algorithm)]] 등을 사용한다. IonQ에서 발표한 11 큐비트 양자 컴퓨터에서 10 큐비트에 대한 번스타인-바지라니 알고리듬을 구현해본 결과, 그 정확도가 평균 78%로 측정되었다는 발표가 있었고 (2019) <ref name=Wright>K. Wright ''et al''., Benchmarking an 11-qubit quantum computer, Nature Communications '''10''', 5464 (2019). doi:[https://doi.org/10.1038/s41467-019-13534-2 10.1038/s41467-019-13534-2].</ref>, 최근에는 80% 이상으로 개선되기도 하였다 (2021).<ref name=Blinov>S. Blinov, B. Wu, and C. Monroe, Comparison of cloud-based ion trap and superconducting quantum computer architectures, arXiv:[https://arxiv.org/abs/2102.00371 2102.00371].</ref> IBM의 5 큐비트 양자 컴퓨터 ibmqx4에서 그로버 알고리듬을 구현해본 결과 정확도가 평균 65%로 측정되었으며, IBM의 ibmqx4와 16 큐비트 양자 컴퓨터 ibmqx5에서 2비트의 숨겨진 수에 대한 번스타인-바지라니 알고리듬을 실행했을 때는, 임의의 수가 “01”, “10”, “11”일 경우 정확도가 각각 38.6%, 44.9%, 43.7%였다 (2018).<ref name=Abhijith>J. Abhijith ''et al''., Quantum algorithm implementations for beginners, arXiv:[https://arxiv.org/abs/1804.03719 1804.03719].</ref> 5 큐비트 IBM 양자 컴퓨터 Vigo에서 4 비트 번스타인-바지라니 알고리듬의 정확도는 [[양자게이트|CNOT 게이트]]의 개수(즉, 숨겨진 임의의 수에서의 1의 개수)에 따라 90% 이상에서 60%대를 보였으며, 15 큐비트 IBM 양자 컴퓨터 Melbourne에서 10 비트의 숨겨진 수에 대한 번스타인-바지라니 알고리듬 테스트에서는 CNOT 게이트 개수가 0일때는 60% 이상이었으나 개수가 늘어날수록 점차 정확도가 낮아져 3개부터는 10% 이하인 것으로 나타났다 (2021).<ref name="Blinov"/> | ||
== | == 기계 학습 (Machine Learning) == | ||
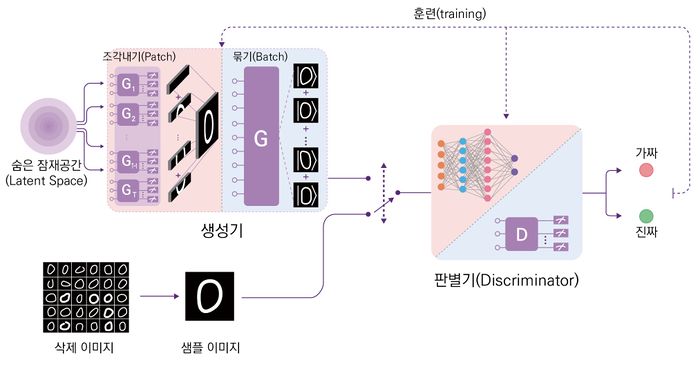
[[File: | [[File:기술백서 전체수정_75_resize.jpg|thumb|700px|GAN(generative adversarial network) 구조.<ref name=Huang>H.-L. Huang ''et al''., Experimental quantum generative adversarial networks for image generation, arXiv:[https://arxiv.org/abs/2010.06201 2010.06201].</ref> 참고문헌 [15]의 그림을 재구성함. | ||
[[양자 알고리듬]]은 암호화 분야뿐만 아니라 | ]] | ||
[[양자 알고리듬]]은 암호화 분야뿐만 아니라 기계 학습 알고리듬에도 기존 알고리듬보다 효율적인 연산이 가능할 것이라고 기대 중이다. 컴퓨터 비전 분야는 기계 학습에 의해 많은 발전을 하게 된 분야 중 하나다. 컴퓨터 비전 분야에서 사용되는 많은 알고리듬 중에 GAN(generative adversarial network)은 이미지 생성을 위한 알고리듬으로, 2014년에 발표된 이후 꾸준히 많은 논문들이 발표되어, 2018년에는 11,800개 논문에 발표되었다. 전체적인 구조는 G(generator)가 이미지를 생성하고, D(discriminator)가 실제 이미지인지 만들어진 이미지인지 구분하는 역할이다. G와 D 둘 다 학습을 통해 정확도를 높인다. | |||
QGAN(quantum generative adversarial network)은 양자 컴퓨터와 기존의 FCNN(fully connected neural network)를 둘 다 사용한 구조이다. GAN의 구조에서 G는 양자 컴퓨터로 구현하고, D를 기존 컴퓨터인 FCNN(fully connected neural network)로 구현했다. 양자 컴퓨터의 [[큐비트]] 수 제한에 맞춰 QGAN과 기존 GAN의 정확도를 비교했다. 학습 결과는 QGAN이 GAN보다 높게 나왔다. | |||
이 외에도 다양한 분야에서 | 이 외에도 다양한 분야에서 양자 컴퓨터가 사용되거나 자체적으로 새로운 알고리듬이 연구 중이다. 아직 양자 우월성을 보이기엔 하드웨어의 한계가 있지만, 한정적인 자원에서 양자 우월성을 보이는 사례도 존재한다. | ||
= 참고 문헌 = | = 참고 문헌 = | ||
2023년 1월 2일 (월) 12:31 기준 최신판
계산 복잡도 (Computational Complexity)[편집]
알고리듬의 수행에 필요한 시간과 메모리 사용량이 입력의 크기에 따라 변화하는 정도를 정량적으로 나타낸다. 전자를 시간 복잡도(time complexity) 후자를 공간 복잡도(space complexity)라고 한다. 계산 복잡도는 특정 문제에 대해 정의되는 것이 아닌 문제를 해결하는 알고리듬에 대하여 정의되며 같은 문제에 대해서도 알고리듬에 따라 다른 시간 복잡도와 공간 복잡도를 가질 수 있다.
- 점근 표기법 (Asymptotic Notation)
알고리듬의 소요 시간이나 메모리 사용이 문제의 크기 $$n$$에 관한 함수 $$f(n)$$ 으로 정의 될때, $$n$$이 커짐에 함수의 증가를 다른 함수와의 점근적 대소관계로 표현하는 방법이다.[1] 큰(big) $$O$$ 표기법, 작은(small) $$o$$ 표기법, 큰(big) $$\Omega$$ 표기법, 작은(small) $$\omega$$ 표기법과 큰(big) $$\Theta$$ 표기법 등이 존재하며 일반적으로 복잡도의 상한을 정의하는 큰(big) $$O$$ 표기법이 가장 범용적으로 사용된다.
- 큰 (Big) $$O$$ 표기법
복잡도가 입력의 크기 $$n$$에 대해 $$f(n)$$이라는 관계를 가질 때, $$f(n) \in O(g(n))$$이라는 것은 다음을 의미한다.
\[\lim_{n \rightarrow \infty}\frac{f(n)}{g(n)} < \infty\]
즉, 충분히 큰 $$n$$에 대해, $$g(n)$$의 상수배가 $$f(n)$$의 상한이라는 것을 의미한다.
- 작은 (Small) $$o$$ 표기법
큰 $$O$$와 유사하지만 $$f(n)$$ 이 $$g(n)$$ 보다 점근적으로 엄격하게 작다(strictly less)는 것을 의미한다.
\[f(n) \in o(g(n)) \Leftrightarrow \lim_{n \rightarrow \infty}\frac{f(n)}{g(n)}= 0\]
- 큰 (Big) $$\Omega$$ 표기법
큰 $$O$$와 반대로 $$f(n)$$이 $$g(n)$$ 보다 점근적으로 크다는 것을 의미한다.
\[f(n) \in \Omega(g(n)) \Leftrightarrow \lim_{n \rightarrow \infty}\left| \frac{f(n)}{g(n)} \right| > 0\]
- 작은 (Small) $$\omega$$ 표기법
작은 $$o$$ 와 마찬가지로 $$f(n)$$이 $$g(n)$$ 보다 엄격하게 크다(strictly large)는 것을 의미한다.
\[f(n) \in \omega(g(n)) \Leftrightarrow \lim_{n \rightarrow \infty}\frac{f(n)}{g(n)}= \infty\]
- 큰 (Big) $$\Theta$$ 표기법
$$f(n)$$이 $$O(g(n))$$이면서 $$\Omega(g(n))$$임을 의미한다. 즉 충분히 큰 $$n$$에 대하여, $$g(n)$$의 두 상수배가 $$f(n)$$의 상한과 하한이 되므로, $$f(n)$$과 $$g(n)$$이 점근적으로 같다는 것을 의미한다.
\[f(n) \in \Theta(g(n)) \Leftrightarrow f(n) \in O(g(n)), f(n) \in \Omega(g(n))\]
일반적으로 기호의 남용임에도 불구하고,
\[f(n) \in O(g(n))\]
인 경우,
\[f(n)= O(g(n))\]
이라고 표기한다. 예를 들어 $$f(n)= an^{2} + bn + c $$일때, $$f(n)= O(n^{2})$$이라 할 수 있는데, 왜냐하면 $$\lim\limits_{n \rightarrow \infty}\frac{f(n)}{n^{2}}= a < \infty$$이기 때문이다.
어떤 알고리듬의 시간 복잡도 $$f(n)$$이 $$O(n^{a})$$ 인 경우 해당 알고리듬은 다룰 수 있는(tractable) 알고리듬으로 분류되고 $$f(n)$$이 $$O(a^{n})$$인 경우에는 다루기 힘든(intractable) 알고리듬으로 분류된다. 다루기 힘든 알고리듬의 경우 $$n$$이 커짐에 따라 소요 시간이 지수적으로 증가하므로 실질적인 의미에서 풀 수 없다고 볼 수 있다.
- P 문제
다항시간의 시간 복잡도를 가진 알고리듬이 발견된 문제들이다. 고전 컴퓨터로 효율적으로 풀 수 있다. 조금 더 정확히 말하면, 다항시간 내에 결정론적으로(deterministically) 풀 수 있는 결정문제(decision problem)이다. 결정문제란 예, 아니오의 형태로 답하는 문제인데, 많은 문제들이 다항시간 안에 결정문제로 변환될 수 있기 때문에 문제 분석에 활용된다.
- NP 문제
답이 주어졌을 때 다항시간의 복잡도로 답을 검증할 수 있는 문제이다. 또는 다항시간 내에 비결정론적(non-deterministically)으로 풀 수 있는 결정문제(non-deterministic polynomial time class)이다. 비결정론적이라는 것은 같은 문제에 대해 알고리듬을 실행할 때 얻는 결과가 달라질 수 있음을 의미한다. 즉, NP 문제는 항상은 아니지만 다항시간 내에 풀 때도 있다는 것이다. P 문제는 다항시간 안에 결정론적으로 해를 구할 수 있으므로 자명하게 NP 문제에 포함되며 P문제에 속하는 것이 증명이 되지 않은 경우 암호화 등에 사용된다. 양자 컴퓨터는 소인수분해나 이산 로그(discrete logarithm)와 같은 NP 문제를 다항시간내에 풀 수 있기 때문에 기존에 사용되는 암호화 알고리듬을 무력화할 가능성이 크다. 양자 알고리듬의 고전 컴퓨터 알고리듬에 대한 우위는 동일한 알고리듬이 양자 컴퓨터에서 더 나은 수행시간으로 실행가능한지로부터 말할 수 있는 것이 아니라, 동일한 문제가 양자 컴퓨터에서 더 나은 시간 복잡도를 가질 수 있다는 사실로부터 나온다고 할 수 있다.
양자 푸리에 변환 (Quantum Fourier Transform)[편집]
양자 푸리에 변환은 이산 푸리에 변환(discrete Fourier transform)
\[y_{k} = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1}x_j e^{\frac{2 \pi ijk}{N}}\]
을 양자 컴퓨터를 통해 수행하는 알고리즘이다.
일반적으로 이산 푸리에 변환이 길이가 $$N(= 2^{n})$$인 배열(array)에 대해 정의되는 것에 비해 양자 푸리에 변환은 직교 기저(orthonormal basis) $$\left| \left. 0 \right\rangle \right. $$, …, $$\left| \left. N - 1 \right\rangle \right. $$에 대해 다음과 같이 정의된다.
\[\begin{align*} \left. |j \right\rangle \overset{\text{QFT}}{\rightarrow}\frac{1}{\sqrt{N}}\sum_{k= 0}^{N - 1}{e^{\frac{2\pi ijk}{N}}\left. |k \right\rangle} &= \frac{1}{\sqrt{N}} \sum_{k_{1} =0}^{1}\ldots\sum_{k_{n}= 0}^{1}{e^{2\pi ij(\sum_{l =1}^{n}{k_{l}2^{- l}})}\left. |k_{1}\ldots k_{n} \right\rangle} \\ &= \frac{1}{\sqrt{N}} \sum_{k_{1} =0}^{1}\ldots\sum_{k_{n}= 0}^{1}{\otimes_{l =1}^{n}e^{2\pi ijk_{l}2^{- l}}\left. |k_{l} \right\rangle} \\ &= \frac{1}{\sqrt{N}} \otimes_{l =1}^{n}\left\lbrack \sum_{k_{l}= 0}^{1}{e^{2\pi ijk_{l}2^{- l}}\left. |k_{l} \right\rangle} \right\rbrack \\ &= \frac{1}{\sqrt{N}} \otimes_{l =1}^{n}\left\lbrack \left. |0 \right\rangle + e^{2\pi ijk_{l}2^{- l}}\left. |1 \right\rangle \right\rbrack \\ &= \frac{\left( \left. |0 \right\rangle + e^{2\pi ij0.j_{n}}\left. |1 \right\rangle \right)\ldots\left( \left. |0 \right\rangle + e^{2\pi ij0.{j_{1}\ldots j}_{n}}\left. |1 \right\rangle \right)}{\sqrt{N}} \\ \end{align*}\]
알고리듬의 시간 복잡도는 $$O( \left( \log N \right)^{2})$$으로 (또는 $$O(n^{2})$$) 고전 컴퓨터에서 고속 푸리에 변환의 시간 복잡도 $$O(N\log{N)}$$에 비해 지수적으로 빠르게 수행된다.
- 구현
하다마드 게이트(Hadamard gate)와 조건부 위상 게이트(controlled phase gate)로 구성된다. 게이트에 대한 보다 상세한 내용은 양자 게이트를 참고하라.
- 하다마드 게이트 (Hadamard Gate)
기본적인 중첩 상태를 만드는 게이트로 계산 기저(computational basis)에 대하여 다음과 같이 정의된다.
\[H= \frac{1}{\sqrt{2}}\begin{pmatrix}1 & 1 \\ 1 & -1 \\ \end{pmatrix}\]
- 조건부 위상 게이트 (Controlled Phase Gate)
조건부 큐비트의 값에 따라 항등 게이트(identity gate)로 작용하거나 특정 각도의 회전으로 작용한다. 특정 각도 회전 게이트는 계산 기저에 대해 다음과 같이 표현된다.
\[R_{m}= \begin{pmatrix} 1 & 0 \\ 0 & e^{\frac{2\pi i}{2^{m}}}\\ \end{pmatrix}\]
각 큐비트가 알고리듬이 요구하는 상태가 되기 위해서는 $$i$$번째 큐비트가 $$n - i + 1$$개의 게이트를 필요로 하기 때문에 전체 필요한 게이트의 수는 다음과 같다.
\[\sum_{i= 1}^{n}{(n - i + 1)} =\frac{n(n + 1)}{2}\]
즉, 게이트의 수는 큐비트 개수의 제곱에 비례하게 증가하며 큐비트의 개수는 입력 크기의 로그에 비례하여 증가한다. 따라서 시간 복잡도는 $$O( \left( \log N \right)^{2} )$$ 이며 공간 복잡도는 추가적인 큐비트를 필요로 하지 않기 때문에 $$O(\log N)$$이다.

양자 위상 추정 (Quantum Phase Estimation)[편집]
양자 푸리에 변환을 이용하여 특정 유니타리(unitary) 연산자 $$U$$의 고윳값(eigenvalue) $$e^{2\pi i\varphi}$$ 을 추정하는 알고리듬을 양자 위상 추정이라고 한다. 고윳값에 해당하는 고유벡터(eigenvector) $$\left| \left. u \right\rangle \right. $$와 controlled-$$U^{2^{j}}$$ 게이트가 주어졌다고 가정하자. 양자 위상 추정 알고리듬은 위상 추정을 위한 $$t$$개의 큐비트와 $$\left| \left. u \right\rangle \right. $$를 표현하기 위해 필요한 큐비트를 사용한다.
- 구현
$$t$$개의 큐비트를 $$\left| \left. 0 \right\rangle \right. $$으로 초기화한 후 하다마드 게이트를 적용한다. 이후 $$t$$개의 큐비트를 컨트롤로 하여 $$t$$개의 controlled-$$U^{2^{j}}$$ 게이트를 아래 그림에서와 같이 적절히 수행하면 출력은 다음과 같은 형태가 된다.
\[\frac{1}{2^{\frac{t}{2}}}\left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{t - 1}\varphi}\left| \left. 1 \right\rangle \right. \right)\left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{t - 2}\varphi}\left| \left. 1 \right\rangle \right. \right)\ldots \left( \left| \left. 0 \right\rangle \right. + e^{2\pi i 2^{0}\varphi}\left| \left. 1 \right\rangle \right. \right) = \frac{1}{2^{\frac{t}{2}}}\sum_{k =0}^{2^{t} - 1}{e^{2\pi i\varphi k}\left| \left. k \right\rangle \right. }\]
해당 출력에 역 양자 푸리에 변환(inverse QFT)을 적용할 때 출력은 다음과 같다.
\[\frac{1}{2^{\frac{t}{2}}}\sum_{k= 0}^{2^{t} - 1}{e^{2\pi i\varphi k}\left| \left. k \right\rangle \right. } \rightarrow \left| \left. \widetilde{\varphi} \right\rangle \right. \]
여기에서 $$\widetilde{\varphi}$$는 $$\varphi$$의 $$t$$-비트 근사값이 된다. 따라서 $$t$$개의 큐비트를 측정하면 고윳값 $$\varphi$$의 근사값을 얻는다.

각각의 controlled-$$U^{2^{j}}$$ 게이트가 상수시간으로 실행됨을 가정하면 시간 복잡도는 양자 푸리에 변환과 동일하게 $$O(t^{2})$$이 된다. $$U$$게이트의 고윳값이 $$t$$개의 큐비트로 나타낼 수 없는 경우에는 추정에 사용하는 큐비트의 개수를 늘림으로써 정확도를 상승시킬 수 있다.
만약 $$1 - \varepsilon$$의 확률로 $$2^{- n}$$의 정밀도로 올바른 추정값을 얻기 위해서는
\[t= n + \left\lceil \log\left( 2 + \frac{1}{2\varepsilon} \right) \right\rceil\]
쇼어 알고리듬 (Shor’s Algorithm)[편집]
$$n$$비트로 표현되는 자연수를 고전 컴퓨터로 소인수분해하는 알고리듬은 $$O(\text{exp}\left( n^{\frac{1}{3}}\log^{\frac{2}{3}}n \right))$$ 의 시간 복잡도를 가진다. 이러한 계산 복잡도는 지수적이므로 큰 수를 소인수분해하는 것은 다루기 힘든(intractable) 문제로 여겨지며 이는 현재 가장 대중적으로 사용되는 공개키 알고리듬인 RSA 알고리듬의 기반이 된다. 그러나 쇼어 알고리듬은 양자 푸리에 변환을 이용하여 $$O(n^{2}\log{n\log{\log{n)}}}$$의 시간 복잡도로 $$n$$비트 자연수의 소인수분해를 수행할 수 있다. 이는 다항시간이므로 현재 사용되는 암호화를 손쉽게 무력화할 수 있을 것으로 예상되며 이는 양자 컴퓨터의 킬러 애플리케이션이 될 것으로 예상된다.
- 차수 찾기 알고리듬 (Order Finding Algorithm)
어떤 수 $$x$$의 모듈로 $$N$$에 관한 차수(order of $$x$$ modulo $$N$$)는
\[x^{r} \equiv 1 \left( \text{mod}\,N \right)\]
을 만족하는 가장 작은 자연수 $$r$$로 정의된다.
양자 위상 추정 알고리듬을 사용하면 $$O(\left( \log N \right)^{3})$$의 시간 복잡도로 계산할 수 있다.[4] 쇼어 알고리듬은 차수 찾기 알고리듬을 통해 효율적으로 소인수의 후보를 탐색하는 방식으로 작동한다.
- 구현
$$\left| \left. j \right\rangle \right. \left| \left. k \right\rangle \right. \rightarrow \left| \left. j \right\rangle \right. \left| \left. x^{j} k\, \text{mod}\, N \right\rangle \right. $$ 으로 변환하는 블랙박스 $$U_{x}$$가 구현되어 있다고 가정하자. $$t= 2L + 1 + \left\lceil \log(2 + 1/2\varepsilon) \right\rceil $$개의 양자 위상 추정을 위한 큐비트를 사용하면 $$O(L^{3}{) }$$의 시간 복잡도로 차수를 계산할 수 있다. 여기서 $$L{ =\left\lceil \log N \right\rceil\text{ }}$$이라고 한다. 쇼어 알고리듬은 $$x$$를 랜덤하게 선택하여 $$N$$의 소인수분해를 시도한다. 만약 $$x^{r} \equiv 1 \left( \text{mod}\,N \right)$$ 일 때, $$r$$이 짝수인 경우 $$\left( x^{\frac{r}{2}} - 1 \right)\left( x^{\frac{r}{2}} + 1 \right) \equiv 0 \left( \text{mod}\,N \right)$$ 이므로 $$\text{gcd}(\left( x^{\frac{r}{2}} - 1 \right), N)$$과 $$\text{gcd}(\left( x^{\frac{r}{2}} + 1 \right), N)$$을 계산하여 1이 아닌 최대공약수를 갖는다면 해당 자연수로 $$N$$을 인수분해한다. $$r$$이 홀수인 경우 다른 $$x$$를 선택한다.
이러한 과정을 반복하면 다항시간으로 $$N$$을 소인수분해할 수 있음이 알려져 있다.[4] 간단하게 동작 원리를 알아 보면, 먼저 양자 위상 추정을 사용하기 위해 $$U_{a}$$의 고윳값과 고유벡터가 어떻게 되는지를 살펴봐야 한다. 그러면 $$s \in \{ 0,1,\ldots,r - 1\}$$ 에 대하여 고유벡터와 고윳값은 각각 $$\left| \left. u_{s} \right\rangle \right.= \frac{1}{\sqrt{r}}\sum_{j =0}^{r - 1}e^{- \frac{2\pi isj}{r}}\left| \left. a^{j}\,\text{mod}\,N \right\rangle \right. $$과 $$e^{\frac{2\pi is}{r}}$$이 됨을 알 수 있다. 이 때 모든 고유벡터를 중첩시키면 $$\frac{1}{\sqrt{r}}\sum_{s= 0}^{r - 1}\left| \left. u_{s} \right\rangle \right. =\left| \left. 1 \right\rangle \right. $$이 된다. 그렇기 때문에 아래 그림에서 양자 위상 추정을 위한 고유벡터로 $$\left| \left. 1 \right\rangle \right. $$을 사용한 것이다. 이렇게 하면 양자 위상 추정을 통해 $$s/r$$를 추정할 수 있고, 이를 통해 $$r$$ 값을 추정하여 위에서 언급한 방법대로 인수분해가 가능한지 검사한다.
현재 큰 수의 소인수분해가 어렵다는 것은 RSA 암호를 비롯한 공개키 암호의 근간을 이루므로 해당 알고리듬은 현재 발견된 양자 알고리듬 중 가장 유용한 킬러 애플리케이션으로 여겨진다.

그로버 알고리듬 (Grover’s Algorithm)[편집]
그로버 알고리듬은 앞서 소개한 양자 푸리에 변환 기반 알고리듬과 함께 현재 알려진 양자 알고리듬의 두 가지 축 중 하나이다. $$N$$개의 원소에 대해 정의된 함수 $$f(x)= 1$$의 해인 $$M$$개의 $$x$$를 찾는 알고리즘이며, 앞서 소개된 알고리듬과 달리 지수적인 속도 상승을 보여주지는 못하지만 고전적 알고리듬보다 제곱근의 시간 복잡도를 갖는다.
- 구현
입력 $$\left| \left. x \right\rangle \right. \left| \left. q \right\rangle \right. $$ 에 대하여 출력 $$\left| \left. x \right\rangle \right. \left| \left. f(x) \oplus q \right\rangle \right. $$ 를 내보내는 오라클(oracle) $$O$$ 가 존재한다고 가정하자.
- 하다마드 게이트를 사용하여 $$\left| \left. 0 \right\rangle \right. ^{\otimes n}$$을 $${\frac{1}{\sqrt{2^{n}}}\left( \left. \left| 0 \right. \right\rangle + \left. \left| 1 \right. \right\rangle \right)}^{\otimes n}$$으로 변환, 보조 큐비트 $$\left| \left. q \right\rangle \right. $$는 $$\left| \left. 1 \right\rangle \right. $$에 하다마드 게이트를 사용하여 $$\frac{1}{\sqrt{2}}\left( \left. \left| 0 \right. \right\rangle - \left. \left| 1 \right. \right\rangle \right)$$로 변환
- 오라클 $$O$$를 적용
- $$\left| \left. x \right\rangle \right. $$에 대하여 하다마드 게이트를 적용
- 조건부 위상 변조(conditional phase shift)를 적용하여 $$\left| \left. x \right\rangle \right. \rightarrow - ( - 1)^{\delta _{x0}}\left| \left. x \right\rangle \right. $$ 로 변환(여기에서 $$\delta$$는 크로네커 델타)
- $$\left| \left. x \right\rangle \right. $$에 대하여 하다마드 게이트를 적용
- 2)~5) 를 반복 적용한 후 측정하여 $$f(x)= 1$$인 $$x$$를 얻음
3)~5) 과정은 ‘평균에 대한 반전(inversion about average)’ 이라고 불리며, 모든 계산기저의 평균이라고 할 수 있는 1) 단계 이후의 상태에 대해 뒤집는 변환을 말한다. 해당 상태는 하다마드 게이트에 의해 $$\left| \left. 0 \right\rangle \right. ^{\otimes n}$$으로 변환되므로 4) 단계의 앞뒤로 하다마드 게이트를 적용하여 평균에 대한 반전을 구현할 수 있다. 이러한 과정은 찾고자 하는 해가 측정될 확률을 증폭시켜줄 수 있는데, 2) 단계에서 오라클에 의해 $$f(x)= 1$$인 $$\left| \left. x \right\rangle \right. $$들의 위상이 뒤집히기 때문이다. 그러나 일정 횟수 이상 실행하면 오히려 확률을 떨어뜨리기 때문에, 매번 증폭시키지는 않는다.
2)~5) 과정은 해 공간(solution space)에서 $$\theta$$ 회전에 해당하며,
\[\sin\theta= \frac{2\sqrt{M(N - M) }}{N}\]
$$M \ll N$$이면,
\[\theta \approx \sin\theta \approx 2\sqrt{\frac{M}{N}}\]
최대 $$\frac{\pi}{2} $$의 회전이 필요하므로 $$\theta$$ 회전의 개수는,
\[R \leq \left\lceil \frac{\pi}{4}\sqrt{\frac{N}{M}} \right\rceil\]
이다. 따라서 시간 복잡도는 $$O(\sqrt{N/M})$$ 이며 이는 고전 컴퓨터 알고리듬의 시간 복잡도 $$O(\frac{N}{M})$$ 에 비해 제곱근만큼 빠르게 작동한다. 이는 그로버 알고리듬이 $$N$$개의 입력을 동시에 처리함을 보여준다. 그러나 이를 위해서는 적절한 오라클을 구현하는 것이 중요하다.

양자 기계 학습 (Quantum Machine Learning)[편집]
양자 이점을 기계 학습에 적용하려는 노력은 최근 부상하고 있으나 현재 기반이 되는 하드웨어의 부재로 인해 이론적인 연구로서만 존재하고 있다. 어떠한 알고리듬이 실제로 구현 가능할 것인지는 아직 명확하지 않으며 본문에서는 제안된 몇 가지 알고리듬을 소개하고자 한다.
- 양자 진폭 시뮬레이션 (Quantum Amplitude Simulation)
고전 컴퓨터에 작동하는 기계 학습 알고리듬을 양자 컴퓨터로 효율적으로 시뮬레이션하면서 이점을 얻으려는 시도로서 대표적으로 행렬계산을 효율적으로 수행함을 목표로 한다. $$n$$개의 큐비트는 $$2^{n}$$개의 상태를 저장할 수 있기 때문에 큐비트 개수에 대해 다항시간의 시간 복잡도를 가진 알고리듬을 사용하여 기계 학습에 사용되는 계산을 수행할 수 있다면 지수적인 시간 복잡도 상승을 얻을 수 있다. 예를 들어 HHL 알고리듬은 특정 조건을 만족하는 행렬의 역행렬 계산을 행렬의 차원의 로그에 해당하는 복잡도로 수행할 수 있다.[7] 이는 고전 컴퓨터 알고리듬의 $$O(n^{2})$$의 복잡도에 비해 지수적인 속도상승을 보여준다. 현재 시뮬레이션 수행의 가장 큰 난관은 데이터를 양자 상태로 변환하는 것으로 아직 일반적인 데이터를 변환할 때 $$O( n^{2})$$ 이상의 시간 복잡도가 필요하므로 실제적인 이점을 얻기 위해서는 해당 부분에서 새로운 알고리듬이 고안되어야 할 것이다.
- 그로버 알고리듬 기반 기계 학습
그로버 알고리듬은 $$N$$개의 원소 중 조건을 만족하는 원소를 고전 알고리듬에 비해 제곱배로 빠르게 찾아낼 수 있으므로 $$k$$-median 이나 $$k$$-nearest neighbor 와 같은 문제를 방대한 데이터셋에서 빠르게 찾아낼 수 있을 것으로 기대된다.[8][9]
- 양자 신경망 (Quantum Neural Network)
고전 신경망을 양자 컴퓨터로 구현하여 양자역학적 효과를 학습 알고리듬으로 사용하는 것을 목적으로 한다. 퍼셉트론(perceptron)을 양자 컴퓨터로 구현하기위해 입출력간 비선형성을 가진 회로를 구현하는 연구가 활발히 진행중이다.[10]
다른 접근방식으로 그로버 알고리듬 기반으로 연관 메모리(associative memory)를 구현하려는 시도가 있다.[11] 즉 입력과 가장 비슷한 메모리를 그로버 알고리듬을 통해 찾아내는 방식으로 작동한다. 이러한 방식은 메모리의 크기가 큐비트의 개수에 지수적으로 증가하므로 효율적인 저장이 가능하다는 이점을 가지고 있다. 그러나 이 모델의 유용성은 이러한 단순화된 연관 메모리가 실질적인 효용을 가진다는 것을 실증하는데에 있으며 이는 실제 양자 컴퓨터나 그러한 양자 컴퓨터를 시뮬레이션 할 수 있는 고전 컴퓨터를 통해서만 입증될 것이다.
최신 성능 개괄[편집]
양자 알고리듬 (Quantum Algorithm)[편집]
양자 알고리듬은 쇼어 알고리듬(Shor’s algorithm)이 나타나면서 각광받기 시작했다. 쇼어 알고리듬은 양자 푸리에 변환(quantum fourier transform)을 기반으로, 소인수분해나 이산대수문제를 기존 컴퓨터보다 기하급수적으로 빠른 속도로 연산이 가능하다. 그리고 현재 사용되는 암호화 알고리듬은 RSA 알고리듬(Rivest-Shamir-Adleman algorithm)으로, 큰 정수의 소인수분해가 기존 컴퓨터로는 어렵다는 점에 착안해서 만들어진 방식이다. 이로 인해 양자 컴퓨터에 대비해서 암호화 분야에는 비상이 걸리고, 양자 컴퓨터는 각광을 받기 시작한다. 양자 컴퓨터의 성능이 좋아지면 기존 암호화 방식인 RSA 알고리듬이 무력화될 가능성이 있지만, 아직은 양자 컴퓨터는 많은 수의 큐비트 구현이 불가능해서 기존 암호화 방식을 위협하기엔 시간이 걸린다.
많이 알려진 양자 알고리듬 중에서 번스타인-바지라니 알고리듬(Bernstein-Vazirani algorithm)도 있다. 이는 임의의 수를 정하고, 이 수를 맞추는 알고리듬으로 기존 방식으로 연산하는 것보다 연산 단계가 적다. 예를 들어 4 비트의 길이를 갖는 숨겨진 임의의 수를 1001이라고 하자. 기존 알고리듬은 먼저 임의의 수와 0001을 비교한다. AND(1, 1)은 1이므로 첫번째 수가 1이라는 것을 알 수 있다. 다음으로 0010와 비교하며 각 비트를 비교한 후에 임의의 수를 알아낼 수 있다. 총 비교 수는 비트 수만큼 반복한다. 하지만 번스타인-바지라니 알고리듬은 큐비트의 수에 상관없이 단 한번의 연산으로 임의의 수를 알아낼 수 있다. 실용성 외에도, 이러한 알고리듬은 양자 우월성을 입증하고 양자 컴퓨터의 기하 급수적인 속도 향상을 증명하기도 한다.
현재는 양자 컴퓨터의 성능을 비교, 판단할 때 쇼어 알고리듬(Shor’s algorithm), 번스타인-바지라니 알고리듬(Bernstein-Vazirani algorithm), 그로버 알고리듬(Grover’s algorithm) 등을 사용한다. IonQ에서 발표한 11 큐비트 양자 컴퓨터에서 10 큐비트에 대한 번스타인-바지라니 알고리듬을 구현해본 결과, 그 정확도가 평균 78%로 측정되었다는 발표가 있었고 (2019) [12], 최근에는 80% 이상으로 개선되기도 하였다 (2021).[13] IBM의 5 큐비트 양자 컴퓨터 ibmqx4에서 그로버 알고리듬을 구현해본 결과 정확도가 평균 65%로 측정되었으며, IBM의 ibmqx4와 16 큐비트 양자 컴퓨터 ibmqx5에서 2비트의 숨겨진 수에 대한 번스타인-바지라니 알고리듬을 실행했을 때는, 임의의 수가 “01”, “10”, “11”일 경우 정확도가 각각 38.6%, 44.9%, 43.7%였다 (2018).[14] 5 큐비트 IBM 양자 컴퓨터 Vigo에서 4 비트 번스타인-바지라니 알고리듬의 정확도는 CNOT 게이트의 개수(즉, 숨겨진 임의의 수에서의 1의 개수)에 따라 90% 이상에서 60%대를 보였으며, 15 큐비트 IBM 양자 컴퓨터 Melbourne에서 10 비트의 숨겨진 수에 대한 번스타인-바지라니 알고리듬 테스트에서는 CNOT 게이트 개수가 0일때는 60% 이상이었으나 개수가 늘어날수록 점차 정확도가 낮아져 3개부터는 10% 이하인 것으로 나타났다 (2021).[13]
기계 학습 (Machine Learning)[편집]
양자 알고리듬은 암호화 분야뿐만 아니라 기계 학습 알고리듬에도 기존 알고리듬보다 효율적인 연산이 가능할 것이라고 기대 중이다. 컴퓨터 비전 분야는 기계 학습에 의해 많은 발전을 하게 된 분야 중 하나다. 컴퓨터 비전 분야에서 사용되는 많은 알고리듬 중에 GAN(generative adversarial network)은 이미지 생성을 위한 알고리듬으로, 2014년에 발표된 이후 꾸준히 많은 논문들이 발표되어, 2018년에는 11,800개 논문에 발표되었다. 전체적인 구조는 G(generator)가 이미지를 생성하고, D(discriminator)가 실제 이미지인지 만들어진 이미지인지 구분하는 역할이다. G와 D 둘 다 학습을 통해 정확도를 높인다.
QGAN(quantum generative adversarial network)은 양자 컴퓨터와 기존의 FCNN(fully connected neural network)를 둘 다 사용한 구조이다. GAN의 구조에서 G는 양자 컴퓨터로 구현하고, D를 기존 컴퓨터인 FCNN(fully connected neural network)로 구현했다. 양자 컴퓨터의 큐비트 수 제한에 맞춰 QGAN과 기존 GAN의 정확도를 비교했다. 학습 결과는 QGAN이 GAN보다 높게 나왔다.
이 외에도 다양한 분야에서 양자 컴퓨터가 사용되거나 자체적으로 새로운 알고리듬이 연구 중이다. 아직 양자 우월성을 보이기엔 하드웨어의 한계가 있지만, 한정적인 자원에서 양자 우월성을 보이는 사례도 존재한다.
참고 문헌[편집]
- ↑ T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein, Introduction to algorithms (MIT press, 2009).
- ↑ https://en.wikipedia.org/wiki/Quantum_Fourier_transform
- ↑ https://en.wikipedia.org/wiki/Quantum_phase_estimation_algorithm
- ↑ 4.0 4.1 4.2 M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information (Cambridge University Press, 2002)
- ↑ https://en.wikipedia.org/wiki/Shor%27s_algorithm
- ↑ https://en.wikipedia.org/wiki/Grover%27s_algorithm
- ↑ A. Harrow, Quantum algorithm for solving linear systems of equations, in Proceedings of APS March Meeting 2010 55, 2 (2010).
- ↑ E. Aïmeur, G. Brassard, and S. Gambs, Quantum speed-up for unsupervised learning, Machine Learning 90, 261 (2013). doi:10.1007/s10994-012-5316-5.
- ↑ N. Wiebe, A. Kapoor, and K. Svore, Quantum algorithms for nearest-neighbor methods for supervised and unsupervised learning, arXiv:1401.2142.
- ↑ S. Gupta and R. K. P. Zia, Quantum neural networks, Journal of Computer and System Sciences 63, 355 (2001). doi:10.1006/jcss.2001.1769.
- ↑ D. Ventura and T. Martinez, Quantum associative memory, Information Sciences 124, 273 (2000). doi:10.1016/S0020-0255(99)00101-2.
- ↑ K. Wright et al., Benchmarking an 11-qubit quantum computer, Nature Communications 10, 5464 (2019). doi:10.1038/s41467-019-13534-2.
- ↑ 13.0 13.1 S. Blinov, B. Wu, and C. Monroe, Comparison of cloud-based ion trap and superconducting quantum computer architectures, arXiv:2102.00371.
- ↑ J. Abhijith et al., Quantum algorithm implementations for beginners, arXiv:1804.03719.
- ↑ H.-L. Huang et al., Experimental quantum generative adversarial networks for image generation, arXiv:2010.06201.