양자 센서 (Quantum Sensor)

<양자 기술백서 |

       ┗|양자컴퓨팅의 구현>

              ┗<양자 시뮬레이션 (Quantum Simulation)|양자 네트워크 (Quantum Network)>

=양자 계측 (Quantum Metrology)

양자 계측 (Quantum Metrology)

계측 (Metrology) 이란?

계측이란 우리가 알고자 하는 정보를 얻기 위해 물리량을 측정하고 추정하는 총체적인 과정을 뜻한다. 국제단위계를 정의하고 측정하는 문제를 비롯해서, 자기공명영상 촬영, 바이러스 진단 검사, 군사 목표물 감지, 지질조사, 자율 차 및 드론 센서, 중력파 검출 등과 같이 측정과 관련된 문제들을 전반적으로 다룬다. 양자 계측(quantum metrology)이란 양자 계(quantum system)만이 갖는 성질[예: 양자 얽힘(quantum entanglement), 조임(squeezing), 양자화된 에너지 준위(level), 결맞음(coherence) 등]을 활용하여 고전 계(classical system)로는 달성할 수 없거나 혹은 제한된 조건에서 더 뛰어난 민감도(sensitivity), 정밀도(precision), 분해능(resolution)을 달성하는 방법을 연구하는 분야이다.

양자 계측은 계측 대상과의 상호작용을 겪은 양자 시스템의 변화를 살펴보는 것으로, 그 방식에 따라 편의상 두 가지 종류로 나눌 수 있다. 첫째, 양자 빛을 계측 대상에 입사시키고, 투과 혹은 반사된 빛의 양자 상태의 변화를 살펴보는 방법이다 [그림1(a) 참조]. 둘째, 계측 대상의 영향을 받고 있는 양자 시스템에 고전 빛을 입사시키고, 투과 혹은 반사된 빛의 특성을 살펴보는 방법이다 [그림1(b) 참조] 양자 계측은 위 분류와 관계없이 일반적으로 네 가지 단계로 이해할 수 있다 (그림2 참조).

1) 양자 상태 초기화(initialization): 계측 대상과 상호작용할 양자계의 초기 상태를 적절히 준비한다.

2) 상호작용(interaction): 위에서 준비된 양자 계를 적절한 방법을 통해서 계측 대상과 상호작용시킨다. 이 과정을 통해서 양자 계의 상태 변화가 발생한다.

3) 측정(measurement): 적절한 측정 장치를 사용해서, 양자계의 상태의 변화를 측정한다.

4) 추정(estimation): 적절한 추정자(estimator)를 사용해서, 측정값을 토대로 실제 값을 추정한다.

따라서, 좋은 계측을 하기 위해서는 각 단계들을 적절하게 혹은 최적의 방법으로 수행하는 것이 필요하다. 이를테면, 계측에 유용한 양자적 특성을 가진 양자 상태를 준비하거나, 상호작용의 세기를 키우거나, 가장 많은 정보를 줄 수 있는 측정을 수행하거나, 가장 좋은 추정 방법을 사용할 수 있다. 최적의 방법론을 찾고, 실험적으로 구현하는 것이 양자 계측 연구의 핵심이다.

계측 오차

계측을 통해 얻어낸 추정(estimation) 값들과 실제(true) 값의 평균적인 차이를 통해서 계측의 성능을 살펴볼 수 있다. 이는 평균 제곱 오차(mean squared error)를 통해 정량화 가능하고, 다음과 같이 정의된다. \[\text{MSE}[\hat{x}]= \langle(x_{\text{est}} - x )^2 \rangle \] 여기서 $$x_{\text{est}}$$ 크기가 $$\nu$$인 표본에 대한 측정 결과들을 토대로 실제 값 $$x$$를 추정 한 값이고 $$\langle \cdots \rangle $$는 크기가 $$\nu$$인 모든 표본에 대한 평균이다. 위 식은 아래와 같이 전개가 가능하며 \[\text{MSE}[\hat{x}]= \langle(x_{\text{est}} - \langle x_{\text{est}} \rangle )^2 \rangle + \langle( \langle x_{\text{est}} \rangle - x )^2 \rangle \] 이때 첫 번째 항의 추정 값의 분산 $$\Delta x^{2}_{\text{est}} $$으로, 다양한 표본에 대한 추정 값들이 서로 얼마나 비슷한 지 나타내는 정밀도(precision)와 관련이 있다 (그림 3 참조). 그리고 두 번째 항은 추정 값이 평균적으로 실제 값과 얼마나 가까운지를 나타내는 정확도(accuracy)와 관련이 있다. 정확도는 계측 장치의 보정과 관련되어 있으며 대개의 경우 $$\langle x_{\text{est}}\rangle=x $$를 만족시키는 비편향 추정자(unbiased estimator)를 사용하기 때문에, 이 경우 $$\text{MSE}[\hat{x}] = \Delta x^{2}_{\text{est}}$$이므로 평균 제곱 오차를 계측의 정밀도로 취급한다.

상황에 따라 $$\Delta x^{2}_{\text{est}}$$를 추정 오차(estimation error), 추정 정밀도(estimation precision), 추정 불확정도(estimation uncertainty)라 부르기도 한다. 그리고 $$\Delta x^{2}_{\text{est}}$$값이 작으면, 실제 값의 변화를 실험적으로 더 민감하게 감지할 수 있기 때문에, $$\Delta x^{2}_{\text{est}}$$를 때로는 민감도(sensitivity)라 부르기도 한다.

크래머-라오 (Cramér-Rao) 부등식

계측(그림 2 참조)에서 비편향 추정자를 사용하는 경우에, 계측오차 $$\Delta x^{2}_{\text{est}}$$는 크래머-라오 한계(Cramér-Rao bound - CRB)라 불리는 하한(lower bound)을 갖고, 이는 다음과 같이 표현된다. \[\Delta x^{2}_{\text{est}} \geq \frac{1}{\nu F(x)} \] 여기서 $$\nu$$는 측정 횟수(즉, 표본의 크기), $$F(x)$$는 $$F(x)=\sum_{y} \frac{1}{p(y|x)}\left(\frac{\partial p(y|x)}{\partial x} \right)^2$$으로 정의된 피셔 정보(Fisher information)이고, $$p(y|x)$$는 실제 값이 $$x$$일 때 측정값 $$y$$를 얻을 확률이다. 측정값 $$y$$를 얻을 확률이다. 측정값 $$y$$가 연속적인 값을 갖는 경우에는 피셔 정보의 정의에서 $$\sum_y$$는 $$\int dy$$로, 확률 $$p(y|x)$$는 확률 밀도 함수로 대체된다. 여기서 피셔 정보는 측정값으로부터 얻어낼 수 있는 $$x$$에 대한 정보량을 뜻한다. 위의 부등식을 크래머-라오 부등식이라 부르고, CRB는 가장 좋은 비편향 추정자를 사용하면 도달할 수 있다. 특별히, 최대 가능성 추정자(maximum-likelihood estimator)를 사용하면 $$\nu$$가 매우 클 때 CRB에 일반적으로 도달할 수 있다. 따라서, CRB는 주어진 초기 양자 상태, 상호작용, 측정 방법에 대해서 최적의 비편향 추정자를 사용해서 도달 가능한 계측 오차 값이다.

피셔 정보 $$F(x)$$는 물리 계, 상호작용, 그리고 측정 방법에 의존한다. 만약, 최적의 측정 방법을 사용하는 경우에는 피셔 정보 $$F(x)$$값을 최대화할 수 있고, 이에 따라 계측 오차의 하한을 더욱 낮출 수 있으며, 다음과 같이 표현된다. \[\Delta x^{2}_{\text{est}} \geq \frac{1}{\nu F(x)} \geq \frac{1}{\nu F_{\text{Q}}(x)} \] 여기서 $$\F_{\text{Q}}(x)$$는 최적의 측정 방법에 의해 최대화된 피셔 정보이고, 이를 양자 피셔 정보(quantum Fisher information)라 부른다. 그리고 더 낮아진 하한을 양자 크래머-라오 한계 (Quantum Cramér-Rao bound - QCRB)라 부르고, 위 부등식을 양자 크래머-라오 부등식이라 부른다. 따라서, QCRB는 주어진 초기 양자 상태와 상호작용에 대해서, 최적의 측정 방법과 최적의 비편향 추정자를 사용해서 도달 가능한 계측 오차 값이다.

양자 피셔 정보는 $$\F_{\text{Q}}(x)$$는 초기 양자 상태와 상호작용의 종류에 따라 다른 값을 가지는데, 특정 상호작용 형태가 주어져 있을 때, 최적의 양자 상태를 사용을 하면 양자 피셔 정보를 최대화할 수 있고, 이에 따라 계측오차의 하한을 궁극적으로 낮출 수 있다. \[\Delta x^{2}_{\text{est}} \geq \frac{1}{\nu F(x)} \geq \frac{1}{\nu F_{\text{Q}}(x)} \geq \frac{1}{\nu F_{\text{UQL}}(x)} \] 여기서 $$F_{\text{UQL}}(x)$$는 최적의 양자 상태에 의해 최대화된 양자 피셔 정보이다. 이 하한의 의미는 주어진 상호작용에 대해서, 최적의 초기 양자 상태와 최적의 측정 방법과 최적의 비편향 추정자를 사용해서 도달 가능한 계측 오차이며, 이를 궁극적 양자 한계 (ultimate quantum limit)라 부르기도 한다.

표준 양자 한계 (Standard quantum limit)과 하이젠베르크 스케일링(Heisenberg scaling)

크래머-라오 부등식을 통해서 알 수 있듯이, 양자 계측에서는 적절한 초기 양자 상태와 적절한 측정 방법을 사용하면, 고전적인 방법보다 계측 오차를 더 낮출 수 있다. 이에 대한 정량적인 비교 분석을 위해, 고전 상태를 사용하는 계측의 QCRB와 양자 상태를 사용하는 계측의 QCRB를 비교한다.

고전상태를 사용하는 계측의 QCRB는 고전상태의 평균 에너지($$N$$)에 반비례($$\Delta x^{2}_{\text{est}} \propto N^{-1}$$)한다. 특별히, 최적의 고전 상태에 의해 최소화된 QCRB를 표준 양자 한계(standard quantum limit)라고 부르며, 이 용어는 Caves의 1981년 PRD 논문에서 표준 측정 장비들을 이용했을 때 달성할 수 있는 계측의 한계라는 뜻으로 사용되었다. () 양자 상태를 사용하는 계측의 QCRB는, 사용하는 양자 상태에 따라서 표준 양자한 계보다 크거나 작을 수 있다. 적절한 양자 상태를 사용하면, QCRB가 양자 상태의 평균 에너지의 제곱(($$N^2$$))에 반비례($$\Delta x^{2}_{\text{est}} \propto N^{-2}$$)하는 경우들을 볼 수 있는데, 이와 같은 스케일링을 특별히 하이젠베르크 스케일링이라 부른다. 최근의 몇몇 연구들은 하이젠베르크 스케일링을 뛰어넘는 계측 오차($$\Delta x^{2}_{\text{est}} \propto N^{n<-2}$$)에 대한 결과를 보고하기도 하였지만, 계측에 사용된 전체적인 리소스 관점에서 $$N$$을 엄밀하게 정의할 경우, 하이젠베르크 스케일링보다 더 큰 스케일링은 불가능하다는 연구가 보고된 적이 있다.

빛을 사용한 양자 계측

여러가지 양자 상태들의 소개

본격적인 논의에 앞서 고전역학과 양자역학의 관계를 간단히 살펴보자. 우리가 고전역학에서 소위 물리량이라 부르던 것들은 양자역학으로 넘어오면서 연산자로 바뀌고 입자의 양자 상태와 함께 그 평균과 표준편차로 기술이 된다. 예를 들어 고전적으로 어떤 입자의 위치가 $$X$$였다면 이를 양자역학적으로 기술할 때에는 어떤 입자의 양자 상태가 $$\vert \psi \rangle$$이며 그 평균과 표준편차가 각각 $$\sqrt{\langle \psi \vert (\Delta \hat{X})^{2} \vert \psi \rangle} $$임을 이야기한다. 고전적인 빛 또한 마찬가지이다. 이제는 모두가 잘 알겠지만 빛은 파동이기도 하지만 동시에 입자이기도 해서 일명 대표적인 보손 (Boson) 입자 중 하나이고 양자 상태로써 기술 가능하다. 따라서 고전 전자기학에서 전기장과 자기장으로 기술되던 빛은 양자역학에서는 빛의 양자 상태, 전기장 연산자, 자기장 연산자의 평균과 표준편차로 기술된다. 그리고 이때 전기장 연산자와 자기장 연산자는 하이젠베르크 불확정성 원리가 성립한다. ($$\hat{X}$$와 $$\hat{P}$$의 관계와 같다.) 다양한 분야에서 가장 많이 사용되고 있는 계측의 매개체는 빛이다. 이는 빛이 갖는 다양한 장점들(제작 및 측정의 용이함, 빠른 전송 속도 등) 때문이다. 따라서 빛의 몇 가지 양자 상태를 살펴보자.

결맞음 상태 (Coherent state)

결맞음 상태는 QCRB의 고전 한계를 정의할 때 주로 고려된다. 그 이유는 여러 고전적인 빛 중에서 결맞음 상태를 사용하는 것이 가장 작은 계측 오차를 달성할 수 있기 때문이다. 결맞음 상태의 전자기장 연산자($$\hat{X}$$, $$\hat{P}$$)의 평균들은 고전 전자기학에서 광원이 없는 전자기장과 완벽하게 동일한 형식을 가지며, 둘의 표준편차는 갖고 그 곱은 하이젠베르크 불확정성 원리에서의 등식을 만족시킨다. 이 때문에 결맞음 상태는 가장 고전적인 양자 상태로 알려져 있다. 이는 위상공간 상에서 잘 나타난다. 세기가 $$\vert\alpha\vert^2$$인($$\alpha$$는 복소수이다.) 빛에 해당되는 상태는($$\vert\alpha\rangle$$으로 나타낸다.) 위상공간 상에서 $$x$$와 $$p$$에 대해서 각각 평균이 $$\text{Re}(\alpha)$$와 $$\text{Im}(\alpha)$$이고 표준편차는 $$\sqrt{\frac{1}{2}}$$인 가우스 분포를 따른다. 추가적으로 말하자면 진공 상태는 $$\alpha=0$$인 경우에 해당한다. 또한 결맞음 상태를 광자 기저들을 이용해 나타내면 다음과 같다. \[ \vert\alpha\rangle = e^{-\frac{\vert \alpha \vert^2}{2}} \sum_{n=0}^{\infty} \frac{\alpha^n}{\sqrt{n!}} \vert n \rangle \] 여기서 $$\vert n \rangle$$는 $$n$$개의 광자를 나타내는 상태이다. 따라서 결맞음 상태의 광재 개수가 푸아송(Poisson) 분포를 따른다는 것을 확인할 수 있다. \[ P_{n} = e^{-\vert \alpha \vert^2} \frac{\vert \alpha \vert^{2n}}{n!} \]

조임 상태 (Squeezed state)

조임 상태 (Squeezed state)는 위상공간 (Phase space)에서 전자기장을 특정 방향에 대해서 찌그러트린 상태를 지칭한다. (Squeezed state 리뷰 논문 첨부) 이와 같은 양자 상태는 찌그러진 방향에 대한 위상 불확정도가 진공 혹은 결맞음 상태보다 더 작기 때문에, 위상 계측에서 유용한 상태로 활용된다. (대표적으로 Caves가 제안한 중력파 검출 방법에 사용된다.) 예를 들어, 조임 진공 상태 (Squeezed vacuum state)는 전자기장의 평균들이 0이고, 하이젠베르크 불확정성 원리를 만족시키면서 전기장 혹은 자기장의 표준편차를 늘리고 나머지 하나의 표준편차는 줄이는 양자 상태이다. 진공 상태의 경우, 위상공간 상에서 $$x$$와 $$p$$에 대해 평균이 $$0$$이고 표준편차가 $$\sqrt{\frac{1}{2}}$$인 가우스 분포를 따른다. 여기에 조임 (Squeezing)을 가하는 경우, 평균은 그대로 지만(만약 진공 상태가 아니라 일반적인 결맞음 상태를 조인 경우 평균도 줄어들고 늘어날 것이다.) 특정 방향의 표준편차는 $$e^{2r}$$만큼 증가하고 이에 수직한 방향의 표준편차는 $$e^{-2r}$$만큼 감소함을 볼 수 있다. 또한 조임 진공 상태를 광자 기저들을 이용해 나타내면 다음과 같다. \[\vert \xi \rangle = \frac{1}{\sqrt{\cosh{r}}} \sum_{n=0}^{\infty} {\tanh^{n}{r}} \]

양자 센싱 (Quantum Sensing)

양자 센싱은 다음의 세가지 센싱 방식을 포함한다. 1) 에너지 준위 등 양자화 된 물리량을이용해 물리적인 값을 측정한다. 2) 양자 결맞음을 이용하여 물리적인 값을 측정한다. 3) 양자 얽힘 등의 성질을 이용해 고전 센싱보다 민감도와 정확도를 올려준다.

양자 센서는 다음 4가지 조건을 만족해야 한다. 1) 양자 시스템의 에너지 준위가 양자화 되어 있으며 2) 특정 상태로 만들거나 읽을 수 있어야 하며 3) 일관되게 조작할 수 있어야 하며 4) 전기장이나 자기장과 같은 물리적인 조건과 상호작용을 할 수 있어야 한다.

양자 센서에 대한 해밀토니안은 다음과 같이 나타낼 수 있다.

\[H(t)= H_{0} + H_{V}(t) + H_{\text{control}}(t)\]

$$H_{0}$$는 원래 시스템이 가지고 있는 해밀토니안이고 이를 알고 있다고 가정한다. $$H_{\text{control}}(t)$$는 양자 센서 조작을 위한 해밀토니안이다. 궁극적으로 센싱 Hamiltonain $$H_{V}(t)$$을 통해 포텐셜 $$V(t)$$를 검출하는 것이 양자 센서의 목표이다. 이를 도출하기 위한 일반화된 센싱 프로토콜은 다음과 같다.

1) 센서를 $$\left| \left. 0 \right\rangle \right. $$으로 초기화를 해준다.

2) 해밀토니안 조작을 통해 $$H_{\text{control}}\left( t_{0} \right)$$을 합당한 시간동안 켰다 꺼서, 시간 변화 유니테리 연산이 수행되어 원하는 상태로 준비한다. 즉, $$\left| \left. \psi_{0} \right\rangle \right.= U(t)\left| \left. 0 \right\rangle \right. .$$

3) 양자 센서를 특정 시간 $$t$$동안 센싱하도록 킨다. 이에 따라 센싱 해밀토니안 $$H_{V}(t)$$에 의한 시간 변화 유니테리 연산이 수행되며 센서의 상태는 $$\left| \left. \psi(t) \right\rangle \right.= c_{0}\left| \left. \psi_{0} \right\rangle \right. + c_{1}\left| \left. \psi_{1} \right\rangle \right. $$ 이 된다.

4) 2)번에서 수행한 유니테리 연산($$U(t)$$)을 역으로 되돌려, 즉 $$\left| 0 \right\rangle= U^{\dagger}(t)\left| \psi_{0} \right\rangle$$ 그리고 $$\left| 1 \right\rangle =U^{\dagger}(t)\left| \psi_{1} \right\rangle$$로 되돌려준다. 그러면, $$U^{\dagger}(t)\left| \left. \psi(t) \right\rangle \right.= c_{0}^{'}\left| \left. 0 \right\rangle \right. + c_{1}^{'}\left| \left. 1 \right\rangle \right. $$ 상태가 된다.

5) 측정기저 $$\left| 0 \right\rangle$$과 $$\left| 1 \right\rangle$$로 측정을 수행하고 그 결과를 기록한다.

6) 1)~5)을 N번 반복하여 베르누이 과정을 통해 전이 확률을 추정할 수 있다.

7) 시간에 따른 전이 확률을 통해 원하는 신호를 추론할 수 있다.

다음은 정적인 신호를 측정하는 대표적인 방법인 라비 측정(Rabi measurement)과 람지 측정(Ramsey measurement) 두 가지와 동적인 신호를 측정하는 동적 디커플링, 그리고 양자 센서가 가지는 내재적인 요인들을 소개한다.

라비 측정 (Rabi Measurement)

첫 번째 예제인 라비 측정은 다음과 같은 프로토콜을 따른다. 1) 양자 센서를 초기화 한다. 즉, 양자 상태 $$\left| 0 \right\rangle$$에 있도록 준비한다. 라비 측정의 경우 특정 상태를 만들 필요는 없기에 과정 2) 와 4)는 생략한다. 3) t초 동안 외부 포텐셜 해밀토니안 $$H_{V}(t)$$을 켜준다. 5) 측정을 통해 전이 확률 $$p= \left| c_{1}^{'} \right|^{2}$$를 구한다. 이때 $$p =\frac{w_{1}^{2}}{w_{1}^{2} + w_{0}^{2}}{ \sin^{2}}\left( \sqrt{w_{1}^{2} + w_{0}^{2}t} \right)$$임이 알려져 있다. 이를 통해 전이 포텐셜의 정보와 공명 주파수를 알 수 있다.

람지 측정 (Ramsey Measurement)

두 번째 예제인 람지 측정은 다음과 같은 프로토콜을 따른다. 1) 양자 센서를 초기화 한다. 2) $$\frac{\pi}{2}$$ pulse를 가해서 양자 상태 $$\left| \psi_{0} \right\rangle$$에 있도록 준비한다. 3) t초 동안 외부 포텐셜을 제거한 $$H_{0}$$ 해밀토니안을 가한다. 4) 다시 $$\frac{\pi}{2}$$를 가한다. 5) 측정을 한다. 이 때 전이 확률은 $$p= \frac{1}{2}\left\lbrack 1 - \cos\left( w_{0}t \right) \right\rbrack$$이다. 이 과정들을 반복하여 전이 확률을 구하면 역으로 두 상태의 에너지 차이인 $$w_{0}$$를 알 수 있다.

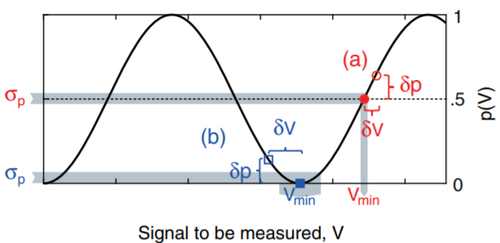
위의 과정을 이용하면 외부의 신호를 측정할 수 있다. 외부 신호 검출은 전이 확률의 변화를 통해 이루어진다. 그림 1은 전이 확률과 포텐셜 변화이 보이는 관계의 예시이다. 확률 변화가 가장 크게 일어나는 곳은 전이 확률이 0.5일 때이므로 이 때를 기준으로 잡아 전이 확률의 변화량을 측정함으로써 포텐셜의 변화량을 측정할 수 있으며 이 경우를 경사 측정이라 한다. 다음은 포텐셜 변화량 $$\delta V$$에 따른 전이 확률 변화 $$\delta p$$에 대한 식이다.

\[\delta p= - \frac{1}{2}\cos\left( w_{0}t + \text{γδ}\text{Vt} \right) \sim \frac{1}{2}\text{γδ}\text{Vt}\]

하지만 포텐셜이 주기적으로 또는 랜덤하게 변해서 변화량의 평균이 0이라면 경사 측정으로는 구별할 수 없을 것이다. 이 경우에는 분산 측정을 이용해야 한다. 분산 측정의 경우 그림 2와 같이 기울기가 0에 가까운 점에서 평균값을 구한다. 그러면 전이 확률의 차이는 0이 되지 않는다. 또한 전이 확률이 0 근처에서 전이 확률은 포텐셜의 제곱에 비례하므로 $$\left\langle \delta V^{2} \right\rangle= V_{\text{rms}}^{2}$$ 를 이용하면 전이 확률이 0인 점을 기준으로 $$V_{\text{rms}}$$를 얻을 수 있을 것이다.

\[\delta p= \left\langle \frac{1}{2}\left( 1 - \cos\left( w_{0}t + \gamma\delta Vt \right) \right) \right\rangle \sim \frac{1}{4}\gamma^{2}V_{\text{rms}}^{2}t^{2}\]

그림 1. 외부 포텐셜과 전이 확률의 모식도. 빨간색 점은 전이 확률 0.5에서 경사 측정시 $$\text{δp}$$의 값을 보여주며 파란색 점은 전이 확률 0에서 분산 측정시 $$\text{δp}$$의 값을 보여준다.

노이즈 (Noise)

측정 값에는 항상 노이즈가 발생할 수 있기 때문에 시스템에서 발생할 수 있는 노이즈가 무엇이 있는지 아는 것은 중요하다. 또한 궁극적으로 노이즈 정보를 통해 SNR (Signal to Noise Ratio)과 이를 통해 시스템의 민감도를 정량적으로 표현하는 최소 측정 가능한 신호를 구할 수 있을 것이다. 다음은 발생할 수 있는 네 가지 대표적인 노이즈 발생 요인들이다.

첫째는 가장 큰 요인 중 하나는 양자 투영 노이즈이다. 양자 시스템은 전이 확률을 구할 때 N번 반복하여 통계를 낸다. 이때 통계를 내는 과정에서 표본 개수 $$N$$이 무한이 아닌 유한이기 때문에 통계 요동(statistical fluctuation)이 발생하고 이에 따라 노이즈가 뒤따라온다. 이항 분포에 따르면 분산 $$\sigma^{2}= \frac{1}{N}p(1 - p)$$ 만큼의 통계적인 노이즈가 발생한다. 예를 들어 람지 선형 측정에서는 $$p =0.5$$이기에 $$\sigma^{2}= \frac{1}{4N}$$ 만큼의 노이즈가 발생한다.

두번째는 측정 시간 동안 발생하는 결어긋남(decoherence)와 이완(relaxation)이다. 이 둘은 무작위로 위상과 상태를 변화시킴으로써 노이즈가 생성된다. 따라서 이전에 측정했던 전이 시간 차이가 시간에 따라 지수적으로 감소한다.

\[\delta p_{\text{obs}}= \delta p(t)e^{- \chi(t)}\]

세번째로는 상태의 초기화와 큐비트 조작에 의한 노이즈이다. 완벽하게 초기화와 큐비트 조작이 어렵기 때문에 발생할 수 있는 노이즈이다. 하지만 결어긋남과는 다르게 측정시간에는 무관하다는 특징을 가진다.

\[\delta p_{\text{obs}}= \beta\delta p\]

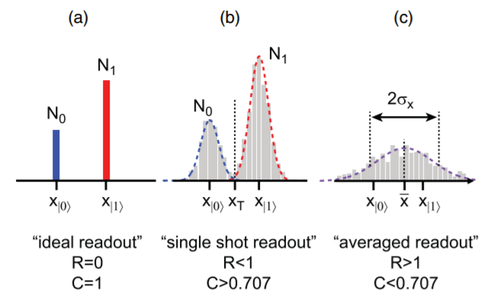
마지막은 측정 도중 발생하는 에러이다. 결과값에 측정된 노이즈에 따라 크게 단일샷 방법과 평균 측정 방법이 있다. 단일샷 방법은 그림 2 (b)와 같이 측정값이 두 값으로 구분할 수 있을 만큼 서로 몰려 있어 기준값을 잡아 결과값을 구분 짓는다. 그림 2 (a)와 같이 이상적인 경우와 비교했을 때 겹치는 부분이 생길 수 있어 이에 따른 측정 노이즈가 발생할 수 있다. $$\kappa_{i}$$는 기준값을 잡아 측정했을 때 부분적으로 포함되지 않는 영역을 의미한다.

\[\sigma_{\text{read}}^{2}= \frac{1}{N}\lbrack\kappa_{0}\left( 1 - \kappa_{0} \right)p + \kappa_{1}(1 - \kappa_{1})(1 - p)\rbrack\]

\[\sigma_{\text{read}}^{2}\sim\frac{\kappa}{N}\]

\[p= \frac{x - x_{|0 >}}{x_{|1 >} - x_{|0 >}}\]

\[\sigma_{\text{read}}^{2}= \frac{R^{2}}{4N}, R =\frac{2\sqrt{N}\sigma_{x}}{|x_{|1 >} - x_{|0 >}|}\]

그림 2. (a) 이상적인 측정인 경우 두 값만이 히스토그램에 나타난다. (b) 싱글샷을 사용하는 경우 기준값 부근에 겹치는 영역이 노이즈가 된다. (c) 첨두치가 하나가 나오는 경우 평균측정법을 이용해 전이확률을 구한다.

민감도 (Sensitivity)

시스템의 민감도란 특정 SNR을 갖는 특정 출력 신호를 생성하는데 필요한 최소 입력 신호를 의미한다. 양자 센싱에서 SNR(Signal to Noise Ratio)는 아래와 같이 정의되며 노이즈에서 얻었던 값을 대입해보면 다음과 같다.

\[SNR= \frac{\delta p_{\text{obs}}}{\sigma} =\delta p(t)e^{- \chi(t)}2C\sqrt{N}\]

람지 측정의 결과를 보면 $$\delta p= \left( \gamma\text{δV}_{\text{rms}} \right)^{q}$$이며 $$q$$에 따라 경사 측정, 분산 측정이 나눠진다. 또한 측정 횟수를 의미하는 $$N$$은 전체 시간 $$T$$에서 측정과 준비를 포함한 시간으로 나눈 것이므로 $$\frac{T}{t + t_{m}}$$과 같다. 이를 종합해 보면 아래와 같다.

\[SNR= \left( \text{γtδV} \right)^{q}e^{- \chi(t)}2C\sqrt{\frac{T}{t + t_{m}}}\]

$$ T= 1$$초동안 단위 SNR에서 최소 측정 가능한 신호는 아래와 같이 쓸 수 있다.

\[v_{\min}^{q} \propto \frac{e^{\chi(t)}\sqrt{t + t_{m}}}{2C(t_{m})\gamma^{q}t^{q}}\]

이 결과를 통해 민감도가 좋은 센서는 다음 조건을 만족해야 한다. 측정 시간은 길수록 좋지만 $$e^{\chi(t)}$$값이 급격히 증가하는 값인 $$e^{\chi(t)}$$의 시간 상수 보다 커지면 안된다. 둘째로 측정 효율 $$C(t_{m})$$은 측정 시간($$t_{m}$$)과 연관되며 측정 효율에 따라 최적의 측정시간을 정할 수 있다. 마지막으로 측정 효율은 실험을 최적화하거나 다른 양자 센싱에 따라 증가될 수 있다.

동적 디커플링 (Dynamical Decoupling)

지금까지는 시간 변화가 없는 정적인 신호에 대한 측정이었지만 시간에 의존적인 신호 역시 측정할 수 있다. 신호가 아래와 같은 신호라 가정하겠다. 이러한 신호의 측정은 람지 위상이라는 것을 이용해 측정한다.

\[V\left( t^{'} \right)= V_{\text{pk}}\cos\left( 2\pi f_{\text{ac}}t^{'} + \alpha \right)\]

\[ \phi= \int_{0}^{t}{\gamma V(t')dt'} \]

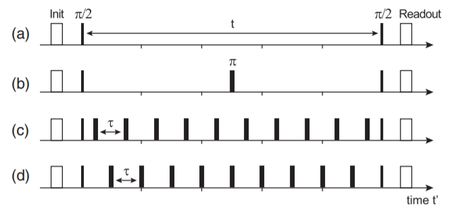
람지 측정의 경우 느리게 변화하는 경우 람지 위상 정보가 남아 있을 수 있다. 하지만 빠르게 변화하는 신호의 경우 위상이 상쇄 간섭에 의해 평균을 취하면 위상 정보가 0에 가까워진다. 또는 측정시간동안 진동의 주기만큼 지난다면 람지 위상은 0이 될 것이다. 다른 시도로는 람지 측정 도중에 $$\pi$$펄스파를 넣어보는 것이다. 그림 3 (b) 과 같이 $$\pi$$ 펄스파를 측정 시간의 정중앙에 두는 과정을 스핀 에코 시퀀스라 하며, 이 경우에는 람지 위상은 $$\phi= \frac{2}{\pi}\gamma V_{\text{pk}}t\cos\alpha$$ 이다. 여기서 아이디어를 착안하여 다중 펄스를 이용하면 더 많은 정보를 알아낼 수 있다. 다중 펄스를 이용했을 때 람지 위상은 다음과 같이 표현할 수 있다. 이 때 $$W$$는 펄스의 배치에 따라 바뀌는 가중치함수이다.

\[\phi= \gamma V_{\text{pk}}tW(f_{\text{ac}},\alpha)\]

다중 펄스 시퀀스의 대표적인 예는 CP(Carr-Purcell)학습과 PDD(Periodic Dynamic Decoupling)이다. CP학습은 그림 3 (c) 과 같이 같이 $$t_{j}= \frac{2j - 1}{2}$$에 펄스파를 두는 방법이고 PDD 방식은 그림 3 (d) 과 같이 $$t_{j} =\text{jτ}$$에 펄스파를 두는 방법이다. 이 두가지 방법의 장점은 파라미터를 조정할 수 있다는 점이다. 또한 신호의 주파수, 결어긋남, $$T_{1}$$, $$T_{2}$$ 이완 등 다양한 정보를 얻을 수 있다. 이 때 전이 확률을 구하면 아래와 같다.

\[p= \frac{1}{2}\lbrack 1 - cos(\frac{\gamma V_{\text{pk}}t\cos\alpha}{\text{kπ}} )\rbrack\]

그림 3. (a) 람지 측정의 펄스 시퀀스. (b) 스핀 에코의 펄스 시퀀스 (c) CP학습의 펄스 시퀀스 (d) PDD의 펄스 시퀀스.