중성 원자 기반

<양자 기술백서 |

       ┗<양자컴퓨팅의 구현|양자컴퓨팅 최신 현황>

              ┗<초전도 큐비트 (Superconducting Qubit)|이온 트랩 (Ion Trap)>

주요 원소 및 특징

원소의 선택에 따라 수행할 수 있는 양자 시뮬레이션이 달라진다. 이는 원소에 따른 에너지 레벨 및 원자간 상호작용의 특징에서 기인한다.

주기율표에 표시한 양자 기체 생성에 성공한 원소들. (내용출처 그림: 위키피디아 수정)

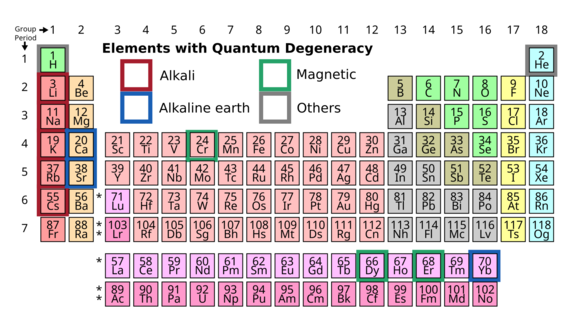
알칼리 금속 (Alkali metal)

수소를 제외한, 최외곽 전자 (valence electron)의 개수가 1개인 원소들을 말한다.

유용한 전이선이 근적외선이나 가시광에 위치하며 상온에서 증기압이 높아 접근성이 좋다. 때문에 역사적으로 많은 연구가 진행되어 왔다.

수소와 마찬가지로 최외곽 전자의 자기모멘트와 핵스핀의 상호작용에 의해 바닥 상태의 원자는 hyperfine splitting을 보이며, 자기장에 예민하게 반응하여 마이크로파로 상태 조종이 가능하다. 세슘 바닥 상태의 hyperfine splitting이 현재 시간 표준의 근간을 이룬다.

상호작용: contact interaction이 주요하다. 모든 안정한 원소들은 유한한 핵 스핀을 가지고 있으며, 보손 및 페르미온이 모두 존재 한다.

알칼리 토금속 (Alkaline-earth metal)

헬륨을 제외한, 최외곽 전자 (valence electron)의 개수가 2개인 원소들을 말한다.

헬륨과 비슷한 에너지 레벨 구조를 가지고 있다. 알칼리 원자에 비해 다채로운 에너지 레벨을 가지고 있으며 magic wavelength가 존재한다. 두 최외곽 전자의 Spin singlet (para-) 과 triplet (ortho-) 간의 다른 홀짝성(parity) 때문에 가시광 영역에서 매우 좁은 선폭의 전이선(clock transition)을 가지고 있는 것이 특징이다. 이를 이용해 optical clock, laser cooling 및 quantum simulation에 응용 연구가 활발히 진행 중이다.

양자컴퓨팅: 바닥 상태의 전자는 singlet을 이루기 때문에 핵과의 hyperfine 상호작용이 거의 없고, 따라서 핵 스핀 상태는 매우 긴 결맞음 시간(coherence time)을 가질 수 있다. 또한 최외곽 전자가 2개이기 때문에 auto-ionization 채널이 존재하며, 이를 이용하여 리드버그상태를 높은 신뢰도로 측정할 수 있다.

상호작용: contact interaction이 주요하다. 보존 원소들은 핵스핀이 0으로 바닥 상태가 자기장에 반응하지 않는 특징이 있다.

자성 원자 (magnetic atoms), 란타넘족 (Lanthanide)

안쪽 껍질 (inner shell)이 완전히 채워지지 않아 큰 자기 모멘트를 가지는 원소를 말한다. 크롬(Cr), 홀뮴(Ho) 등도 큰 자기 모멘트를 가지고 있다. 란타넘족 원자들 중 최외곽 6s를 모두 채우고, 4f 오비탈의 전자들이 원자가 전자인 원자들은 큰 자기 모멘트를 가지고 있다. 최 외곽 6s상태를 채우 고 있는 두 전자 때문에 란타넘족은 알칼리 토금속 원자들과 비슷한 타입의 레이저 전이선을 가지고 있고 알칼리 토금속에서 개발한 테크닉들을 적용할 수 있다.

Contact interaction과 자기 쌍극자-쌍극자 상호작용이 모두 주요한 것이 큰 특징이다. 4f 오비탈의 큰 각운동량 = 자기 모멘트 때문에 다채로운 페쉬바흐 공명이 존재하고, 이를 통해 contact interaction을 억제하면 자기 모멘트가 주요한 다체계 현상을 연구할 수 있다.

극성 분자 (Polar molecule)

강한 전기 쌍극자-쌍극자 상호작용, 분자축의 회전자유도 등 원자에서는 볼 수 없는 고유의 특징을 보유하고 있다. 이를 활용하여 긴 상호작용이 지배적인 계의 양자 시뮬레이션, 강한 상호작용을 컨트롤 할 수 있는 큐비트 시스템의 구축 등의 연구가 기대되고 있다. 극성 분자의 생성 방식에 따라top-down method와 bottom-up method로 구분된다.

Top-down method: 극저온 원자를 준비하는 방식을 그대로 분자로 확장시킨 방법이다. 원하는 분자를 생성 후, 레이저 냉각을 이용하여 분자를 극저온으로 냉각시킨다. 이때 사용되는 분자는 최외각 궤도에 전자가 하나 혹은 두개 존재하는 불안정 분자로, 알칼리 금속 , 알칼리토 금속 원자와 유사한 에너지 구조를 가진다.

Bottom-up method: 나노켈빈의 온도까지 냉각된 두 종류의 원자를 자기장, 레이저를 이용하여 coherent하게 결합시켜서 극저온 분자를 만드는 방법이다. 두가지 알칼리 금속을 결합한 Bi-Alkali 분자, 알칼리 금속과 알칼리토 금속을 결합한 분자가 있다.

중성 원자 제어 기술

중성 원자 실험의 요소

진공 챔버 및 원자 소스

역사적으로 아래 소개하는 두 가지 방식이 많이 사용 되어왔다. 중성 원자를 이용한 센서, 시뮬레이션 등의 활용가치가 높아지면서 진공 챔버와 원자 소스를 결합하는 다양한 방법들이 개발되고 있다.

이중 챔버 시스템

이중 챔버 시스템의 모식도 (출처 KRISS)

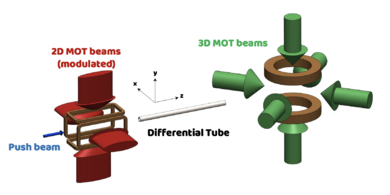
혹은 이중 광자기 포획(Double MOT) 시스템이라고 한다. 다른 진공도를 갖는 두 개의 진공 챔버를 연결하여 제작한다. 낮은 진공도에서는 많은 수의 원자를 광자기 포획을 이용하여 포획, 냉각을 하고, 고 진공의 챔버에서는 낮은 진공에서 포획한 차가운 원자를 이동, 재 포획한 후 보즈-아인슈타인 응축을 제작한다. 일차 광자기 포획에서 고 진공 챔버로 보내는 방법으로는 공명 레이저를 이용하여 원자에 운동량을 주어 보내는 방법, 광학 트위저를 이용하여 보내는 방법, 자기장 코일을 움직이거나 순차적으로 작동하여 원자를 보내는 방법 등이 사용된다. 일차 포획용 챔버에는 낮은 용량의 진공펌프를 사용하고, 이차 포획용 챔버에는 높은 용량의 진공펌프를 연결하고, 두 챔버는 가는 관으로 연결하여 서로 다른 진공도를 유지할 수 있게 된다.

제이만 감속기 (Zeeman Slower, Zeeman Decelerator)

원자빔을 감속시키기 위한 제이만 감속기. 약 1미터 길이의 솔레노이드 형태의 전자석이 도플러 효과를 상쇄하는 자기장을 생성한다. (출처 KAIST)

고온의 원자 빔을 저온의 원자 빔으로 냉각하는 장치로 고 진공 챔버에서 저온의 원자를 포획하는데 사용된다. 원자가 통과하는 원통에 잘 디자인된 자기장을 걸어주고(일반적으로 다양한 밀도로 코일을 감아서 완성한다.) 원자 빔의 반대 방향으로 냉각 레이저를 조사함으로 완성된다. 자기장에 따라 일차 제이만 효과에 의해 원자의 에너지 레벨의 간격이 변하게 되고, 냉각 레이저와 공명 에너지의 주파수 차이, 도플러 효과에 의해 고온의 원자 빔이 저온으로 냉각되게 된다.

레이저

2-준위 원자와 레이저의 상호작용. g, e는 각각 바닥 상태와 여기 상태, γ, Ω, Δ는 각각 여기 상태의 붕괴속도, 레이저-원자 상호 작용 세기, 레이저-원자 주파수 차이를 의미한다.

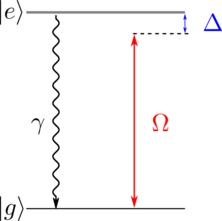
흔히 레이저는 가시광 근처의 파장을 이야기하며 이 대역에서 광자의 운동량은 기체상태의 원자에 상당한 운동량 변화를 줄 수 있다. 이를 잘 활용하여, 레이저 냉각, 레이저 포획 등으로 활용할 수 있다. 레이저와 원자의 상호작용은 공명 여부에 따라 크게 두 가지 다른 양상을 보인다. 이는 2-준위 (two-level system)을 이용해 이해할 수 있으며, 이를 확장하면 수 많은 준위가 존재하는 원자와 레이저의 상호작용을 이해할 수 있다.

• 공명 ( Ω>> γ, Δ) 에너지 간격에 맞는 레이저를 가할 경우, 원자는 레이저로부터 광자를 흡수하여 바닥상태에서 여기상태(excited state)로 전이하게 된다. 흡수 과정에서 광자의 운동량이 원자의 운동량에 전달이 되고 이 운동에너지를 되튐 에너지 (recoil energy) 이라고 한다 (거시적인 수준에서는 복사압 (radiation pressure)). 레이저 냉각 등에 핵심적인 역할을 한다.

• 비 공명 (Ω << γ, Δ) 원자의 전이선에서 많이 벗어난 주파수의 레이저를 가할 경우, 원자의 에너지 준위가 레이저에 의해 살짝 바뀌는 것으로 이해할 수 있다. 이를 AC 슈타르크 이동 (AC Stark shift)이라고 부른다. 레이저를 강하게 집광하면 초점 근처에서만 원자의 에너지 준위가 낮아지며 보존 퍼텐셜(conservative potential)을 형성하여 마치 원자를 (마찰력이 없는) 그릇에 담은 것과 같은 상황이 된다. 광집게, 광격자 등 양자 시뮬레이션의 핵심 원리 이다.

  

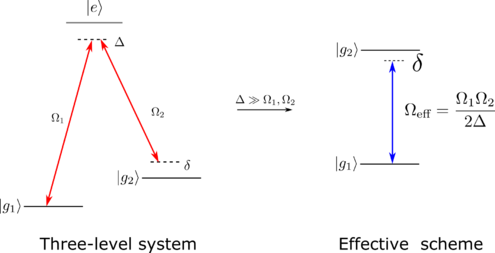
  3-준위 원자와 2개의 레이저의 상호작용. 표기한 조건에서 3-준위 시스템은 근사적으로 2-준위 시스템으로 기술된다. 본 그림과 같이 두 바닥 상태의 에너지 상태가 광학 주파수보다 훨씬 작을 때를 라만 전이라고 한다.

3-준위 원자와 이광자 전이

3-레벨 원자와 2가지 레이저의 상호작용은 양자 게이트 구현, 레이저 냉각, 인공 게이지 장 생성 등 양자 시뮬레이션에 중요한 역할을 한다. 두 레이저의 디튜닝(detuning), $$\Delta$$이 레이저의 라비 진동수, $$\Omega_{1, 2}$$ 보다 클 때, 2-준위 시스템 처럼 작동한다. 두 개의 광자가 관여하기 때문에 선택 규칙(selection rule)이 좀 더 자유도가 있으며, 직접적으로 전이하는 경우 (단 광자 공명 전이)에 비해 더 크거나 작은 운동량을 원자에 전달 할 수 있는 장점이 있다. 이광자 전이를 활용하여 레이저 냉각, 리드버그 상태 준비 등을 구현할 수 있다. 유효 라비 진동수, $$\Omega_{eff} = \frac{\Omega_1 \Omega_2}{2\Delta}$$을 살펴보면 단 광자 전이에 비해 강한 레이저 세기가 필요함을 알 수 있다.

레이저 광원의 제어

레이저 기술의 발전은 원자 물리 연구에 아주 중요한 요소이다. 새로운 파장의 레이저, 보다 강한, 레이저, 보다 정밀한 레이저 등의 발명은 이전에는 접근하기 어려웠던 원자의 전이선을 탐구하고, 다른 연구에 응용할 수 있게 해준다. 예를 들면, 수 Hz 수준의 선폭을 가진 레이저를 통해 알칼리 토금속의 금지된 (하지만 완전히 금지되지 않은) 전이선을 탐구하고, 이를 원자 냉각, 원자 시계 등에 응용한다.

중성 원자의 실험에서는 다양한 방법으로 레이저를 제어한다. 광펌핑 (optical pumping) 등의 정교한 과정에서는 레이저의 모든 자유도(주파수 및 위상, 세기, 편광, 공간 모드)를 제어하는 것이 중요하다. 다음은 주로 사용하는 소자이다.

• 광 음향 변조기 (Acousto-optic modulator). 흔히 AOM 이라고 부르며, 레이저의 주파수와 세기를 동시에 빠른 (~ 1 μs) 속도로 제어할 수 있다. 투명한 결정질의 매질에 압전소자 (piezo electric material)을 이용하여 라디오 주파수 대역(30 MHz ~ 300 MHz)의 음파를 만들면, 레이저가 해당 주파수의 포논을 흡수하거나 유도방출하여 주파수가 바뀐 빛이 회절된다. 인가하는 라디오 주파수 신호의 주파수나 포락선(envelope) 등을 변조하여 여러 가지 방식의 제어가 가능하여 양자 시뮬레이션에 활용하는 레이저를 제어하기 위해 자주 사용된다.
• 광 전기 변조기 (Electro-optic modulator). 흔히 EOM이라고 부른다. 전기장의 크기에 따라 굴절률이 변하는 매질에 신호를 가하면 소자에 걸린 전기장의 세기에 따라 투과하는 레이저의 위상이 바뀐다. 이를 이용하여 옆띠(side band)를 생성하거나, 편광을 순간적으로 바꾸어 편광판과 함께 짧은 펄스를 만들기도 한다. AOM에 비해 빠른 신호(>GHz)를 인가할 수 있다는 장점이 있다.
• 공간 변조기 (spatial light modulator). 줄여서 SLM이라고도 부른다. 레이저의 공간 모드를 바꾸기 위해 주로 사용된다. 액정을 이용한 소자, MEMS공정을 이용한 Digital micro mirror device 등이 있다. 이를 활용하면 회절 한계 내에서 컴퓨터로 생성할 수 있는 임의의 퍼텐셜을 원자에 가할 수 있어 다양한 용도로 활용할 수 있다.
• 편광 빔 스플리터, 파장판 등의 편광 조절 장치. 복굴절을 이용한 편광 조절을 할 수 있는 소자들을 이용해 빛의 편광 모드를 제어한다.

마이크로파

마이크로파를 이용한 제어는 위의 레이저를 이용한 제어와 유사하다. 알칼리 원자의 초미세 상태를 조종하는 것이 대표적인 예이며, 핵자기 공명(Nuclear magnetic resonance) 방법과 매우 유사하다. 통신 산업 등의 응용 덕분에 발전한 마이크로파 및 라디오 주파수 기술들을 활용하여 실험을 할 수 있고, 레이저를 이용한 제어에 비하여 높은 정확도로 측정하고 좋은 신뢰도로 제어할 수 있다. 대표적인 활용 사례로, 세슘 원자의 바닥 상태의 마이크로파 전이를 이용한 시간 표준이 있다.

정자기장 및 정전기장

제이만 효과 (Zeeman effect)

리튬7의 제이만 효과. F는 핵 스핀(3/2)과 전자 스핀(1/2)을 합친 good quantum number로 초미세 상호작용에 의한 상태를 구별하는데 사용한다.

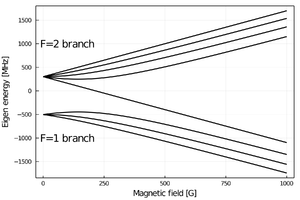
정자기장의 하에서 원자의 서로 다른 자기양자수 상태의 에너지 준위가 달라진다. 이를 제이만 효과라고 한다. 원자의 내재적인 자기 모멘트가 외부 자기장에 의해 반응하는 것으로 이해할 수 있다. 자기모멘트의 크기는 원자 내부의 전하를 가진 입자의 질량에 반비례하며, 원자가 전자(valance electron)의 스핀이 주된 자기 모멘트의 원인이다. 예를 들면, 원자가 전자가 1개인 알칼리 금속의 경우 상태에 크게 상관없이 제이만 효과를 보이고, 알칼리 토금속의 경우 2개의 원자가 전자의 짝짓기(pairing) 상태에 따라 전자에 의한 제이만 효과가 있을 수도(세겹, triplet) 없을 수도(홑겹, singlet) 있다. 제이만 효과에 따른 에너지 준위 변화량, $$U_Z$$는 다음과 같이 쓸 수 있다.

\[ U_Z = -\mathbf{\mu} \cdot \mathbf{B} \]

여기서 $$\mathbf{\mu}$$는 원자의 자기 모멘트로 상태의 자기 양자수에 의존한다. 많이 사용되는 알칼리 금속의 경우, 공통적으로 지구자기장 세기 정도의 세기(100 mG)에서 약 100 kHz 정도 에너지가 달라진다. 실험실에서 일반적으로 얻을 수 있는 라비 진동수(~10 kHz)에 비해 큰 양이며, 정밀한 실험을 위해서는 자기장 차폐나 보상 등 정밀한 자기장 제어기술이 필수적이다.

슈타르크 효과 (Stark effect)

정전기장 하에서 에너지 준위가 달라지는 현상을 슈타르크 효과 라고 한다. 극성 분자를 제외한 원자들의 바닥 상태는 전자 구름이 등방하기 때문에(전자 오비탈이 한 가지 홀짝성(parity) 을 가짐) 영구적인 전기 쌍극자 모멘트(electric dipole moment), $$p$$, 를 가지 않는다. 전기장, $$E$$, 을 가하면, 유도 쌍극자 모멘트가 생성이 되며 ($$p \propto E$$) 유도된 모멘트와 전기장의 상호작용에 의해 에너지 준위가 달라지게 된다. 따라서 에너지 준위의 변화량, $$V_S$$, 은 간략하게 다음과 같이 나타낼 수 있다.

\[ V_S = -\frac{1}{2} \alpha |E|^2 \]

여기서 $$\alpha$$는 원자의 분극률(polarizability)이다. 본 표현은 정전기장 뿐만 아니라, AC 슈타르크 이동에도 쓸 수 있다. 이 경우 분극률은 레이저 주파수의 또는 파장의 함수가 되며, 전기장의 크기는 평균을 이용하면 된다 ($$\alpha \rightarrow \alpha(\omega)$$). 원자의 다양한 전이선 때문에 다양한 분극률을 가지며, 상태에 따라 천이한 분극률을 보이기도 한다 (state-dependent potential, magic wavelength 등). 바닥 상태의 알칼리 금속의 정전기장에 대한 분극률은 160~400 a.u. (atomic unit)을 가지며, 이는 220 V 플러그에 걸리는 전기장(약 110 V/cm)에서 약 500 Hz 정도 이동하고, 이는 자기장에 비해 상대적으로 적은 양이라고 할 수 있다. 하지만, 리드버그 상태로 여기 시킬 경우 전자와 원자핵 간의 먼 거리 때문에 분극률이 매우 크게 증가한다.

온라인 중성 원자 분극률(polarizability) 참조 링크.

극성 분자의 제어 기술

기본적으로 원자에서 쓰이는 모든 제어기술은 그대로 극저온 분자에 적용될 수 있다. 하지만, 분자는 원자에는 없는 분자핵의 진동, 회전자유도를 가지고 있기 때문에, 외부 전자기장에 의한 에너지의 변화를 계산할 때 주의가 필요하다. 또한, 분자의 전이를 고려할 때도 분자핵의 진동, 회전 상태의 변화에 유념해야 한다. 큐비트로 활용할 수 있는 분자의 회전 상태는 마이크로파로 직접 제어할 수 있다.

포획 기술

여기서 포획 기술은 저온으로 냉각된 원자들을 레이저와 자기장으로 이루어진 일종의 그릇(conservative potential)에 담는 기술로, 중성 원자를 이용한 양자 시뮬레이션에서 핵심적인 기술이다. 진공중에서 정전기장이나 정자기장을 이용해 원자를 가두는 것은 자명하지 않기 때문에 (Earnshaw's theorem 참조) 여러 가지 아이디어들이 고안되어 왔다. 현재 가장 널리 사용되는 방법은 자기장을 이용하는 방법과 광학적 방법을(레이저) 이용하는 방법이다. 자기장은 대체적으로 덜 정교하지만, 주어진 자원에서 효율적으로 큰 부피와 깊이를 가지는 퍼텐셜을 형성할 수 있어서 초저온으로 냉각하는 중간 단계에서 많이 사용한다. 광학적 방법을 이용하면 광격자나 홀로그램을 이용한 광집게와 같이 정교한 기술을 사용할 수 있어서 양자 시뮬레이션에 사용한다.

자기장

다양한 코일을 사용하여 자기장의 국소적인 극값(local extreama)을 진공 중에 만들면 제이만 효과에 의해 에너지($$U_Z$$)가 낮은 극값을 중심으로 포획되는 원리이다. 원자의 상태에 따라서 자기 모멘트가 달라지며, 포획이 여부가 결정된다. 여러 가지 아이디어들이 제안되어 왔고 그 중 3가지를 아래에서 소개한다.

시간 평균 회전 (Time-averaged Orbiting Potential; TOP) 포획법

시간 평균 회전(TOP) 포획 법. (좌) 자기 사중극 포획 우물을 회전시켜 원자를 포획한다. (우) 보즈 아인슈타인 응축 실험에 사용된 시간 평균 회전 포획 코일. 참조문헌의 그림을 재구성함.

보즈 아인슈타인 응축에 사용되는 포획 우물들. (좌상) Plug beam을 이용한 포획 우물. (우상) Ioffe type trap. (좌하) Clover leaf type trap. (우하) QUIC trap. 각 참조문헌의 그림을 재구성함.

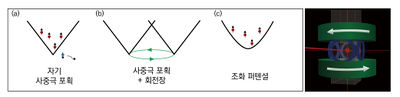
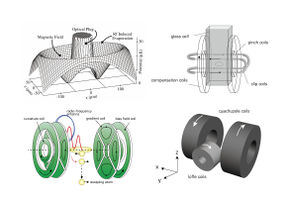
광자기 포획에 사용한 반-헬름홀츠(anti-Helmholtz) 코일을 이용하여 자기 사중극 포획 우물(Mangetic Quadrupole Potential)을 생성한다. 이 포획 우물을 원자의 스핀이 뒤집히는 속도보다 빠르게 회전시키면 원자가 지속적으로 포획되게 되고, 시간 평균으로 보면 자기장이 완벽히 상쇄되는 곳이 없는 포획 우물이 생성되어 마요라나 스핀 플립에 의한 손실을 막을 수 있다.

Ioffe-type Trap

DC 자기장을 이용하여 자기장이 0인 점이 없게 만든 포획법이다. 이 방법은 Clover leaf trap과 단순화 한 QUIC(Quadrupole Ioffe Configuration) 트랩으로 발전되었다.

Plug Beam Trap

강한 공명 주파수 보다 짧은 파장의 레이저(Blue detuned laser)를 자기 사중극 포획 우물 가운데에 조사하여 자기장이 0인 부근에 원자가 접근하지 못하도록 하는 포획법이다.

광집게 (Optical tweezer)

레이저를 강하게 집속하여 원자 구름이나 단 원자를 포획하는 방법을 광집게(optical tweezer)라고 일컫는다. 이는 앞서 언급한 슈타르크 효과의 원리를 통해 이해할 수 있다. 광학 및 레이저 분야에서 연구된 방법론을 활용하여 다양한 모양의 퍼텐셜을 만들 수 있으며, 이를 양자 시뮬레이션에 활용한다.

기본적인 방법은 레이저 빔을 광학계를 이용하여 강하게 집속시키고 여기에 원자를 가두는 것이다. 양자 시뮬레이션을 위해서는 회절 한계 (~1 um)에 준하는 길이 스케일의 정교한 엔지니어링이 필요하다. 초기에는 일반적인 레이저 공진기나 광섬유에서 나오는 빛의 공간모드를 그대로 이용 했었고, 최근에는 이러한 레이저빔을 여러 가지 방식의 빛 공간 변조기 (spatial light modulator)와 회절 한계 성능을 내는 고성능 광학계를 사용하여 원하는 모양의 퍼텐셜을 인가할 수 있다.

광격자 (Optical lattice)

광격자를 이용한 극저온 중성 원자는 고체물질 연구에서 제시된 수 많은 아이디어들을 상대적으로 이상적인 (단순한 해밀토니언, 외부와의 격리 등) 상황에서 시험해볼 수 있는 플랫폼이라 할 수 있다. 중성 원자를 이용한 양자시뮬레이션의 많은 경우가 바로 광격자를 사용하기 때문에 매우 중요한 개념이다.

빛의 간섭 현상을 이용하여 공간상에 주기적인 격자를 만들 수 있는데, 이를 광격자라고 한다. 원자를 포획하는 원리는 광집게와 동일하며, 광집게의 하위 개념으로 생각 할 수 있다. 예를 들어, 한 축에서 서로 마주한 레이저의 경우 1차원 격자를, 두 축에서 조사된 레이저의 경우 2차원 격자를 만들 수 있으며, 3축에서 각각 서로 마주한 레이저를 조사하게 되면 3차원 격자를 만들 수 있다. 또한 레이저 간의 각도를 조절하게 되면 격자의 간격을 조절할 수 있으며 레이저의 세기로 격자의 포획 깊이를 조절하게 된다.

광격자의 형성. 화살표는 각각 인가한 레이저의 진행 방향을 나타낸다. A와 같은 하나의 가우시안 빔을 되반사 시키면 B와 같이 정상파를 이루고 광격자를 형성하게 되고 이를 1차원 광격자라 한다. 수직한 방향으로 다른 레이저를 추가하면 C와 같이 2차원 광격자를 만들 수 있다. D는 일반적으로 실험에서 사용 되는 파라미터에서의 광격자의 모습이며, A-C는 이해를 돕기 위한 그림이다.

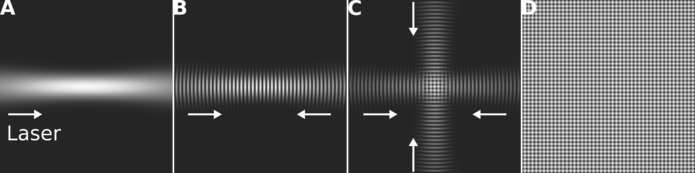
광격자의 간격은 사용한 레이저의 파장과 간섭하는 방식에 의해 결정되며, 레이저 파장의 절반 정도인 약 500 nm가 최소 간격으로 같은 고체 상태의 물질이 구성하는 옴스트롱 단위의 격자구조에 비해 매우 넓다. 하지만 중성 원자 기체는 극저온으로 냉각이 가능하기 때문에 매우 얕은 깊이의 광격자(<< 1 mK)에 원자들을 포획 할 수 있으며, 양자 터널링이 원자 움직임의 주요한 매커니즘이 된다.

대부분의 광격자는 빛의 정상파를 이용하여 생성하며, 레이저의 파장을 안정화 하는 기술이 매우 잘 발달했기 때문에 깨끗한 광격자를 쉽게 만들 수 있다. 간섭 현상을 다방면으로 응용하여 삼각 격자, 육방 격자 등 흥미로운 형태의 격자를 생성할 수 있다. 또한 원자가 움직이는 시간 스케일(약 1ms)에 비해 레이저를 빠르게 (1 μs) 변조할 수 있고, 이를 활용하여 더 확장된 형태의 해밀토니언을 (게이지 장, 플로케 이론, Floquet theory) 시뮬레이션 할 수도 있다.

참고: 광격자 데모 영상

냉각 기술

레이저 냉각 (Laser cooling)

레이저 냉각은 광자의 운동량을 원자에 전달하는 방법을 영리하게 이용하여, 원자의 운동에너지와 그에 따른 원자 구름의 온도를 낮추는 방법을 말한다. 레이저 냉각 기술에는 그 한계에 따라 크게 도플러 냉각 (Doppler cooling,), 그리고 이를 뛰어넘어 원자가 한번의 광자 흡수에서 전달받는 에너지인 되튐 에너지 (recoil energy)수준으로 낮추는 서브-도플러 냉각으로 (sub-Doppler cooling) 나눌 수 있다.

레이저 냉각의 한계는 각각 두 가지 에너지 스케일, 여기 상태의 자연 선폭(에 해당하는 에너지)과 광자의 되튐 에너지가 관여한다. 도플러 냉각의 경우 자연 선폭의 에너지 수준에서 그 한계가 결정되고, 서브-도플러 냉각의 경우 되튐 에너지에 의해 결정된다. 대부분의 레이저 냉각의 경우 여기 상태의 자연 선폭은 약 MHz 단위 되튐 에너지는 kHz 단위로 자연 선폭이 되튐 에너지에 비해 크며, 이러한 상황에서 위와 같은 한계가 결정된다.  

도달할 수 있는 온도와 포획할 수 있는 최대 속도가 서로 이율배반(trade-off) 관계에 있기 때문에 도플러 냉각(광-자기 포획)을 통해 많은 원자를 포획한 뒤, 서브-도플러 냉각으로 추가적으로 냉각하는 방식이 일반적이다.

도플러 냉각

도플러효과를 이용해 레이저 진행방향과 반대방향의 속도를 가진 원자들에게 선택적으로 광자의 운동량을 전달하는 방법이다. 레이저의 에너지(파장 혹은 주파수)를 정지 상태의 원자 전이선에 약간 못미치는 양 만큼 가하면 모자란 에너지를 원자의 운동에너지가 채운다. 이렇게 운동에너지를 채우기 위해서는 레이저의 진행방향과 원자가 마주보는 방향이어야하고, 따라서 원자를 감속하는 쪽으로 광자의 운동량이 전달된다.

속도에 비례하는 감쇠 효과로 광 당밀(optical molasses)이라고도 불린다. 자기장을 이용하면 공간적으로도 국소화 할 수 있고 이를 이용한 것이 광-자기 포획이다. 제이만 감속기 역시 이러한 효과를 활용하여 냉각한다.

도플러 효과를 활용하기 위해서는 원자의 속도를 레이저의 주파수가 분간할 수 있어야 한다. 따라서 자연 선폭이 레이저가 원자의 속도를 분간할 수 있는 한계를 지정하게 되며, 이에 따라 자연 선폭에 해당하는 운동에너지 이하로 냉각할 수 없다. 이를 도플러 한계 (Doppler limit)라고 일컫는다. 알칼리 금속 원자의 경우 이 방법을 이용해 약 수백 mK의 원자들을 약 1 mK 정도로 냉각할 수 있다. 좁은 선폭(100~ 10 kHz)을 가진 알칼리 토금속이나 란타넘족의 원자들을 사용하면 되튐 에너지에 근접한

서브-도플러 냉각

서브-도플러 냉각은 양자광학적인 방법을 사용하여 도플러 냉각의 한계 이하로 레이저 냉각하는 방법을 총칭한다. 편광의 경사를 (polarization gradient) 이용해 시시포스 (Sisyphus) 방식으로 냉각하는 방법, 두 가지 색의 레이저를 이용한 gray molasses 및 전자기 유도 투명성 (Electromagnetic induced transparency) 등을 이용하는 방법 등 다양한 방법들이 존재한다. 이러한 방법들은 모두 속력이 0에 가까운 원자들을 양자광학적 맥락의 암흑 상태(Dark state, 특정 조건이 되면 빛과 더이상 상호작용하지 않아 관찰할 수 없는 상태)로 만드는 방법에 의존한다.

서브-도플러 냉각의 한계는 레이저가 전달할 수 있는 운동량의 최소 분해능, 즉 되튐 에너지에서 기인하고 되튐 한계(recoil limit) 라고 부른다. 기발한 여러 방법을 사용하지만, 결국에는 광자를 흡수시키고 방출시키는 과정을 이용하여 냉각을 하는 것이고, 따라서 레이저가 전달할 수 있는 에너지의 최소 분해능 이하로는 냉각이 어려운 것이다. 이러한 방법을 되튐 에너지 정도인 수 μK 정도로 냉각할 수 있다.

광-자기 포획 (Magneto Optical Trap)

광-자기 포획 개요도. (출처 위키피디아)

광-자기 포획한 원자 구름 사진. 진공 중에 원자 구름이 형광을 내고 있다. (출처 KAIST)

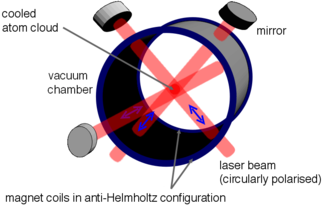
광-자기 포획(Magneto-optical trap, MOT)은 레이저 냉각을 이용하여 온도가 수 마이크로 켈빈인 중성 원자 샘플을 얻을 수 있는 방법이다. 반-헬름홀츠 코일(Anti-Helmholtz coil)을 이용하여 위치에 따라 다른 세기의 자기장을 생성한다. 이는 원자의 제이만 에너지가 위치에 따라 달라, 동일한 주파수의 냉각 레이저에 대해 다른 흡수율을 갖게 된다. 이는 도플러 효과와 함께 위치에 따라 다른 속도의 원자를 냉각하게 되고, 특히 자기장이 0인 중심 부근에서 가장 낮은 온도의 원자를 포획, 냉각하게 된다. 광자기 포획을 이용하여 낮출 수 있는 온도의 한계를 도플러 한계(Doppler Limit)이라고 하며 원자의 natural linewidth의 절반에 해당하는 에너지가 그 한계이다.

증발 냉각 (Evaporation cooling)

증발 냉각의 원리.

증발 냉각은 원자 구름을 시스템의 바닥 상태에 가까운 초저온 상태까지 냉각할 수 있는 방법이다. 흔히 커피가 식는 과정과 비슷하다고 말한다. 먼저 원자를 깊이를 바꿀 수 있는 덫에 준비한다. 광집게를 이용해 포획한 경우 레이저의 세기를 AOM을 이용해 낮추는 것이 깊이를 바꾸는 것에 해당한다. 그런 다음, 덫의 깊이를 낮추면 뜨거운 원자들만 선택적으로 잃어버리게 된다. 그 이후, 원자들이 탄성충돌을 하면서 운동에너지를 재분포하여 평형 상태가 될 때 까지 기다리면 전체 계의 온도가 낮아지는 결과를 얻을 수 있다. 실제 실험 상황에서는 일련의 과정이 연속적으로 동시에 일어나며, 이상적인 상황에서 남은 원자의 개수와 시스템의 온도가 스케일링 법칙을 따른다는 것이 알려져 있다.

실제 실험에서 성공적인 냉각을 위해서는 좋은 충돌 (good collision)이 나쁜 충돌이 (bad collision) 일어나는 속도보다 100배 가량 좋아야 한다고 이야기한다. 좋은 충돌은 원자간의 운동에너지 재분배만 일어나는 탄성 충돌을 이야기하며, 나쁜 충돌은 일반적으로 비탄성 충돌을 말하며 충돌 후 원자를 잃어버리거나 내부 에너지(예를 들면 초미세 구조의 에너지)가 운동에너지로 바뀌는 과정을 말한다. 두 충돌의 비율은 원소의 선택, 원자 상태의 선택, 외부 장에 의한 효과 (페시바흐 공명이나 화학반응) 등에 의해 달라지며, 이를 잘 이해하고 컨트롤 하는 것이 중요하다.

초저온 양자 기체 실험에서 사용되는 샘플의 밀도는 원소에 상관없이 일반적으로 대략 $$10^{19}~{m^{-3}}$$ 전후로 결정되는데, 이는 나쁜 충돌의 세기에 의해 결정된다. 해당 밀도에서 약 수십에서 수천 Hz의 충돌 속도를 가지며, 증발 냉각을 위해 퍼텐셜을 수정하는 시간은 이보다 훨씬 느려야 하기 때문에 보통 1초~10초 정도의 냉각 시간이 소요된다.

측정 기술

동그란 모양의 보스-아인슈타인 응축 상태의 원자 구름의 흡수 사진 측정 과정 (출처 KAIST)

중성 원자 실험에서 원자의 상태를 알아내는 방법은 대부분 원자가 흡수하거나 방출 혹은 굴절하는 빛을 이용한다. 흔히 사용되는 방법 중 하나는 흡수 사진 촬영 방법이다. 원자가 잘 흡수할 수 있는 공명 주파수의 레이저를 조사하면 원자의 그림자를 사진으로 찍을 수 있다 (Signal사진). 이것을 원자 구름이 없는 사진에(Reference사진) 비해 얼마나 흡수 되었는 지를 측정하면, 보는 방향으로 더해진 밀도, Column density를 얻을 수 있다. 강한 레이저 밝기에 따른 원자 반응의 포화 및 확산과 낮은 밝기에서 산탄 잡음(shot noise)간의 저울질에 의해서 한계가 결정된다. 최대 정확도는 약 2-3개의 원자를 분해할 수 있는 수준이지만, 공간적인 해상도를 잃게 된다. 레이저를 조사하는 시간이 짧기 때문에 (1-100 μs) 순간적인 원자 구름의 움직임을 포착하기에 용이하고, 넓은 시야를 가질 수 있다는 장점이 있다.

양자기체 현미경으로 측정한 2차원 원자 구름의 형광 사진. 격자의 간격은 약 0.75 μm이다. (출처 KAIST)

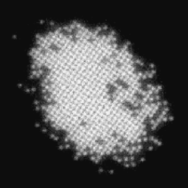
형광을 이용하는 방법도 많이 사용된다. 광-자기 포획에 사용되는 빛을 사용하면 손쉽게 원자 구름을 촬영할 수 있다. 이처럼 레이저 냉각 및 포획에 사용하는 빛을 이용해 촬영을 하면, 긴 시간동안 노출을 통해 손쉽게 산탄 잡음을 이겨낼 수 있다. 하지만 이 과정에서 원자들의 위치와 같은 정보들을 잃게 된다.

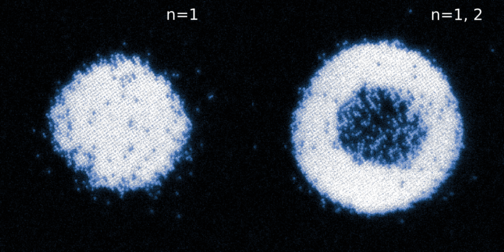
최근에는 레이저 냉각 및 포획 기술의 발전으로 광격자나 작은 광집게에 포획된 상태의 원자들을 촬영할 수 있게 되었다. 이러한 기술을 이용해 양자 기체를 관찰하는 경우를 양자 기체 현미경(quantum gas micrscope) 이라고 한다. 이를 통해 원자의 위치에 대한 분해능과 개수에 대한 분해능을 동시에 달성할 수 있다. 이 시스템의 한계 중 하나는 원자 개수의 홀짝성만 측정한다는 것이다. 즉, 한 격자 위치에 원자가 0개 있는 경우와 2개 있는 경우를 구별할 수 없다는 것이며, 이것은 촬영 과정에서 조사하는 빛에 의한 광접착(Photoassociation) 때문이다. 한 위치에 원자가 짝수 개수가 있으면 모두 짝을지어 도망가고, 홀수 개수가 있으면 하나만 남게 되는 것이다.

이외에도 공명주파수에서 약간 먼 빛을 사용하여 원자의 분산성(dispesion)을 이용한 비파괴 측정이나 공진기에서 새어나오는 광자를 측정함으로써 원자의 상태를 읽어내는 방법 등 여러가지 방법이 존재한다.

중성 원자의 상호작용

중성 원자의 양자 시뮬레이션의 가장 중요한 요소 중 하나는 바로 원자들 간의 상호작용 이라고 할 수 있다. 두 원자 간의 상호작용의 다양한 양상에 의해 시뮬레이션을 수행하는 다체계의 양상이 달라진다. 원소의 선택에 따라 (분자의 경우 조합에 따라) 다양한 상호작용의 양상을 지니고, 제어가 가능하기도 불가능하기도 하므로 이를 잘 이해하는 것이 매우 중요하다.

그 이름에서 알 수 있듯, 중성 원자의 총 전하량이 0이다. 하지만 원자 내부의 전하는 전자 및 원자핵 등의 구조에 의해 어떤 분포를 가지고 있기 때문에, 구조로 부터 생성되는 전기 쌍극자 상호작용이나 자기모멘트(스핀) 간의 상호작용이 가장 유효한 크기를 가진다고 할 수 있다. 알칼리 금속이나 알칼리 토금속 원자들의 바닥 상태는 구형으로 완전히 대칭적이기 때문에 영구적인 전기 쌍극자 모멘트를 가지지 않으며 매우 가까이 (~nm이하) 근접 했을 때에만 상호작용을 한다. 이 경우 원자들의 상호작용을 접촉 상호작용(contact interaction)을 통해 효과적으로 이해할 수 있다.

반면 자성 원자의 경우 큰 자기 모멘트(스핀)를 가지며 이를 통한 쌍극자-쌍극자 상호작용이 지배적인 상황을 만들 수 있다. 이와 비슷하게 극성 분자는 영구적인 전기 쌍극자 모멘트를 가지고 있으며 전기장을 통한 제어를 이용해 양자 시뮬레이션에 이용한다. 원자를 리드버그 상태라 불리는 전자가 원자핵으로 부터 매우 멀리 떨어진 상태로 전자의 편극률이 매우 커지고, 이를 이용하면 매우 강한 상호작용을 만들 수 있다. 상호작용의 범위나 세기 등이 현재 극저온 원자 기술과 잘 맞아 떨어지면서 이를 활용한 양자 컴퓨터 개발이 활발히 진행 중이다.

접촉 상호작용 (Contact interaction)

바닥 상태의 알칼리 금속이나 알칼리 토금속의 경우 원자의 전자 구름 자체가 완전히 구형으로 대칭이므로(s-orbital) 먼 거리에서 가장 유효한 상호작용은 유도 쌍극자간의 상호작용인 판데르발스 (van der Waals) 상호 작용이 가장 유효하다고 할 수 있다. 하지만 두 원자가 가까워 질 수록 그 높은 차수의 상호작용이 기여하면서 실제로는 복잡한 형태의 퍼텐셜을 가진다. 이러한 복잡한 상호작용에도 불구하고, 원자의 크기가 매우 작고 극저온 원자기체의 밀도가 아주 낮다는 점에서 이론적으로 훨씬 간단하게 이해할 수 있다. 바닥 상태의 원자는 전자 구름의 크기는 가장 큰 세슘 원자의 경우 0.3 nm 미만의 반지름을 가지며 이는 일반적인 극저온 원자 샘플의 원자 간 거리인 약 0.5 μm에 크게 못미친다. 이러한 스케일의 차이 때문에 상호 작용 퍼텐셜($$V(\mathbf{r})$$)을 다음과 같은 접촉 상호작용으로 잘 묘사할 수 있다.

\[ V(\mathbf{r}) = \frac{2\pi \hbar^2 a_s}{\mu} \delta (\mathbf{r}) \]

여기서 $$\mathbf{r}$$은 두 원자의 거리 벡터, $$\mu$$ 는 환산 질량이다. $$a_s$$는 s-wave 산란 길이로, 이 숫자 하나에 두 원자의 상호작용에 대한 모든 정보가 들어간다. $$ \delta (\mathbf{r}) $$ 는 디랙-델타 함수로, 두 원자의 파동함수의 겹침 정도를 계산하여 손쉽게 두 원자의 상호작용 에너지를 계산할 수 있게 해준다. 이를 잘 활용하면 원자 구름의 다체계의 해밀토니언을 허바드 모델과 같은 toy model들에 상당한 정확도로 근사할 수 있다. 여기에 더 나아가 페시바흐 공명 현상을 이용하면 $$a_s$$를 넓은 영역에서 바꿀 수 있다.

페시바흐 공명 (Feshbach resonance)

자기장을 이용한 페시바흐 공명 제어의 원리. 분자 상태와 원자 상태의 자기 모멘트의 차이를 이용하여 공명 산란형상을 유도한다.

리튬7 원자의 페쉬바흐 공명.

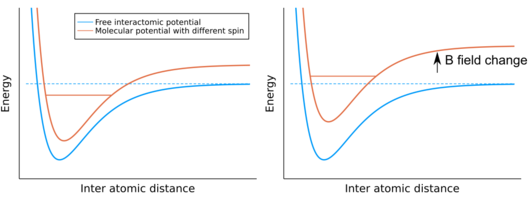
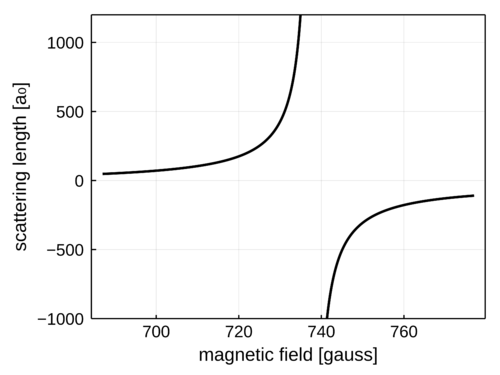
페시바흐 공명, 파노-페시바흐(Fano-Feshbach)공명이라고도 불리는 이 현상은 일종의 공명 산란 현상을 일컫는다. 이를 이용하면 산란 길이, $$a_s$$를 제어할 수 있고 이는 양자 시뮬레이션 실험을 디자인하는 데에 매우 유용하다. 개략적인 원리는 널리 사용되는 자기장을 이용하는 방법을 통해 이해할 수 있다. 자유로운 상태의 두 원자와 (파란색) 다른 자기 모멘트를 가진 분자 퍼텐셜이 (주황색) 존재한다. 두 상태의 퍼텐셜이 서로 다른 자기 모멘트를 가지기 때문에, 둘의 상대적인 에너지 차이를 자기장을 통해 바꿀 수 있다. 그러면 같이 속박 상태 (실선 에너지 레벨)의 에너지 준위가 자유로운 충돌하는 원자의 에너지 상태와 일치하는 순간이 생길 수 있다. 일반적으로 두 원자가 매우 가까워지면, 스핀 성분이 섞이는 채널이 존재하며, 이러한 채널을 통해 충돌에서 공명 현상을 일으킨다. 공명 근처에서 산란하는 파동함수의 위상이 크게 바뀌며 $$a_s$$를 제어할 수 있다.

페르미 통계를 따르는 원자, 특히 $$^6\text{Li}$$의 넓은(=정밀 제어가 가능한) 페시바흐 공명을 이용해 BEC-BCS crossover와 같은 새로운 패러다임의 물리 현상을 실험할 수 있다.

이런 공명현상을 야기시키는 방법에는 다양한 방법들이 알려져있다. 자기장 뿐만 아니라, 빛을 이용한 optical Feshbach resonance, 원자를 비대칭적인 강한 퍼텐셜에 속박하여 궤도를 통해 유도하는 confinement induced Feshbach resonance등이 존재한다. 위와 같이 자기장을 이용하기 위해서는 원자의 자기 모멘트가 자기장에 크게 반응해야하며, 근처에 분자 퍼텐셜이 존재해야하므로 원자의 선택과 함께 활용 가능성이 정해진다. 알칼리 토금속과 같이 전자의 모멘트가 없는 경우, 페시바흐 공명을 사용하기 어려우나 광학적인 방법을 잘 사용할 수 있다.

자성 원자의 경우, 샘플 준비를 위해 $$a_s$$를 크게 유지하다가 본 실험에서는 자기 쌍극자-쌍극자 상호작용의 효과를 상대적으로 크게 보기 위해 $$a_s$$를 낮추는 데에 사용 하기도 한다. 극성 분자의 경우, 자기장에 추가로 전기장이라는 자유도를 사용할 수 있고, 상호작용의 제어나 이해를 확장하고 있다.

원거리 상호작용

리드버그 상태나, 영구적인 쌍극자가 있는 원소들 혹은 광자와 같은 매개체를 활용하면 초저온 원자의 적은 밀도 (~1 μm)에서도 큰 상호작용을 할 수 있다.

리드버그 상태의 판데르발스(van der Waals) 상호작용

87 루비듐 원자의 리드버그 상태 파동함수. $$a_0$$는 보어 반지름을 말한다.

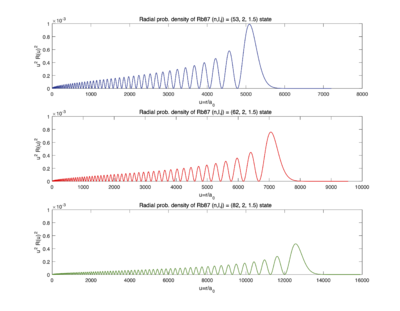
리드버그 상태는 원자가 많은 에너지를 흡수하여 높은 에너지 준위로 여기 된 상태를 말하며, 주 양자수 n이 100정도로 큰 상태를 말한다. 리드버그 원자의 파동함수 크기를 약 10000$$a_0$$(보어 반지름) 혹은 0.5 μm 정도이다. 약 0.2 nm 혹은 4$$a_0$$ 정도의 바닥 상태에 비해 리드버그 상태의 반지름에 비해 매우 크다. 이렇게 커진 반지름으로부터 다음과 같은 성질들을 얻을 수 있다.

• 전기장 혹은 다른 리드버그 원자에 민감하게 반응한다. 전자가 원자 핵으로부터 매우 약하게 구석되어 있기 때문에 전자 구름은 전기장에 민감하게 반응하며, 다른 리드버그 원자가 곁에 있을 경우 쉽게 편극이 된다. 따라서 판데르발스 상호작용의 크기가 바닥 상태에 비해 매우 커지게 된다. 약 5 μm 거리에서 수 GHz에 육박하는 에너지 준위 이동을 보일 수 있다.
• 리드버그 상태의 수명이 길어진다. 광자를 흡수해 여기된 상태의 수명은 다른 준위와의 파동함수 겹침 정도와 그 간격 (photon density of state)에 의해 결정된다. 리드버그 상태는 바닥과의 상태가 매우 적다. 인접한 다른 리드버그 상태와의 파동함수와의 겹침 정도는 크지만 에너지 준위 간의 간격이 좁다.이렇게 해서 리드버그 상태의 수명은 1 ms 정도까지 늘어난다.

강한 상호작용과 긴 수명을 이용해 수 MHz 라비 진동수의 레이저를 이용해 많은 (1 ms / 1 μs) 게이트를 수행할 수 있으며, 이를 활용한 양자 시뮬레이션 및 양자 컴퓨터로 응용하는 연구가 활발하다. 문서 뒷부분에 자세히 다룬다.

자기 및 전기 쌍극자-쌍극자(dipole-dipole) 상호작용

쌍극자-쌍극자 상호작용은 최인접 원자 뿐만 아니라 그 너머에 있는 원자들과도 상호작용 할 수 있고, 비 등방적(anisotropic)으로 상호작용을 한다는 특징을 가지고 있다. 위치 인덱스 $$i$$  와 $$j$$에 있는 두 쌍극자의 상호작용 에너지, $$V_{ij}$$는 다음과 같이 표현할 수 있다.

\[V_{ij} = \frac{1}{4\pi\epsilon_0}\frac{\hat{\mathbf{d}_i} \cdot \hat{\mathbf{d}_j} - 3 (\hat{\mathbf{r}}_{ij} \cdot\hat{\mathbf{d}_i})(\hat{\mathbf{r}}_{ij} \cdot\hat{\mathbf{d}_j}) }{|\mathbf{r}_i - \mathbf{r}_j|^3}\]

광자 매개 상호작용

원자와 빛의 상호작용을 이용하면 원자간의 거리에 구애받지 않는 상호작용을 구현할 수 있다. 핵심 아이디어는 하나의 광자 모드(mode)와 원자를 강하게 상호작용 시키는 것이다. 원자와 광자의 상호작용이 작기 때문에 일반적으로 높은 성능의 공진기가 요구되며, 하나의 광자 모드가 원자 구름과 상호작용하게 한다. 이 때 원자들이 위치와 모드의 상대적인 위치가 중요한데, 크게 두 가지 접근 방식이 있으며 두 방식 모두 모든 원자가 빛의 모드와 동일한 (위상으로) 상호작용하게 만들기 위함이다. 하나는 빛의 파장보다 원자구름을 작게 만드는 것이고, 또 하나는 빛의 파장에 해당하는 주기마다 원자를 위치시켜, 모든 원자가 같은 위상의 빛을 느끼게 하는 것이다.

중성 원자 기반 양자 시뮬레이션

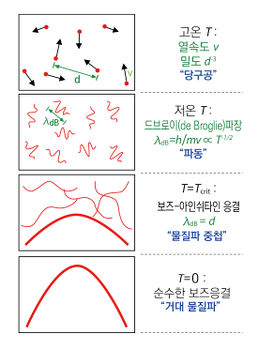
보스-아인슈타인 응축 (Bose-Eisntein condensates)

• 

  보스-아인슈타인 응축을 설명한 그림. 온도를 낮추면 원자들의 상태 함수가 겹치면서 응축이 일어난다.

• 

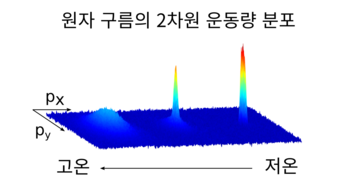
  보스-아인슈타인 응축 과정을 운동량 분포를 통해 관찰한 그림. 온도가 낮아짐에 따라, 원자 구름의 운동량 분포가 맥스웰-볼츠만 분포에서 벗어난다. 바닥 상태로 식은 상태에서도 유한한 운동량을 가지는데, 이는 원자들의 상호 작용 및 위치-운동량 불확정성의 원리 때문이다. (출처 KAIST)

보손 입자는 주어진 상황에서 동일한 상태에 머물 수 있고, 이러한 보손 입자의 에너지를 낮추어 모두 동일한 기저상태를 공유하는 상태를 보즈-아인슈타인 응축이라고 한다. 일반적으로 보손 입자들을 포획 우물에 가둔 후 절대 영도에 가까운 온도로 냉각, 포획 우물의 바닥 상태에 있게 하여 만들 수 있다. 1924-1925년 보즈와 아인슈타인의 논문에 처음 예측이 되었고, 1995년 JILA에서 코넬과 와인먼, 동료 연구원들에 의해 처음 실험적으로 구현이 되었고, 4개월 후 MIT에서 독립적으로 보즈-아인슈타인 응축을 만든 케털리와 함께 2001년 노벨 물리학상을 수상하였다.

광격자 기반 허버드 모형 (Optical lattice based Hubbard model)

깊이에 따른 1차원 광격자($$V\cos^2(kx)$$)의 밴드 구조. $$q$$는 결정 운동량(crystal momentum) 이다.

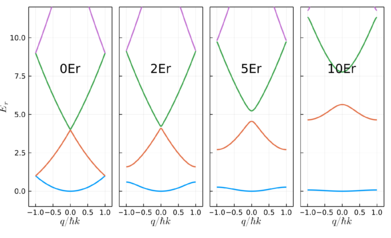
중성 원자를 이용한 양자 시뮬레이션은 많은 경우 광격자 기반의 허버드 모형을 일컫는다.

보스-허버드(Bose-Hubbard) 모형

BEC 생성에 성공하고 얼마 지나지 않아, 광격자를 이용하면 이를 이용해 양자 상전이 (quantum phase transition)을 관찰할 수 있다는 예측이 발표되었고, 얼마 지나지 않아 이를 실험적으로 구현하였다. 초저온으로 냉각된 원자 기체에 광격자를 서서히(adiabatically) 인가하면 광격자의 바닥 밴드(ground band)로 준비할 수 있다. 광격자에 담긴 원자 기체는 국소화된 파동함수에 의해 원자간의 상호작용(이 경우 contact interaction)이 매우 중요해지며 격자구조가 주는 대칭성과 맞물려 흥미로운 다체 현상들을 보인다. 초전도체, 위상 부도체 등의 고체 상태의 물질을 설명하기 위해 개발된 다양한 모형들을 광격자를 이용하여 구현이 가능하다.

밴드갭에 비해 상호작용의 세기가 충분히 작은 경우, 광격자의 중성 원자들은 다음과 같은 헤밀토니언으로 묘사할 수 있다.

\[H_{BH} = -t \sum_{\langle i, j \rangle} { b^{\dagger}_{i}b_{j} + U\sum_{i} \frac{n_{i}(n_{i} - 1)}{2} + \sum_{i} \epsilon_i n_{i} }\]

$$b$$ 는 보손의 소멸 연산자, $$t$$는 터널링 에너지, $$U$$는 한 격자 위치에서의 상호작용에 의한 에너지, $$\epsilon$$은 각 위치에서의 에너지 오프셋 (harnomic curvature 등)을 의미한다.

이중우물의 바닥상태에 대한 묘사. 우물을 가르는 퍼텐셜이 매우 낮을때($$|t|>>U$$), 왼쪽과 같이 퍼진 상태가 기저 상태가 된다. 반대 극한의 경우 ($$|t|>>U$$) 상호작용에 의해 발생할 에너지가 hopping을 유도하는 양자적 요동보다 훨씬 크게 되어 각 우물에 하나씩 원자가 위치하는것이 안정적인 상태를 보인다.

보스-허버드 모형은 광격자 기반의 중성원자 시스템에서 가장 성공적으로 구현한 모델이라고 할 수 있다. 얕은 광격자에서는 하나의 원자의 위치가 여러 격자 위치에 양자역학적으로 퍼지게 되며(delocalized) 이를 초유체 상태라고 한다. 원자가 양자 터널링을 통해 여러 격자 상태에 걸쳐 존재하기 때문에 각 위치 간의 원자상태의 위상이 잘 정의가 된다. 이 상태에서 광격자를 서서히 올리면 각 격자 위치에서 원자간의 상호 작용 에너지, $$U$$, 가 중요해진다. 상호 작용 에너지의 크기가 원자의 운동에너지 혹은 깡충뛰기 에너지(hopping energy), $$t$$, 보다 일정 수준이상 커지면 한 격자안에 여러 원자가 있는 상태의 에너지가 높아지게 되고, 이러한 경우의 수를 피하는 방향이 바닥 상태가 된다. 강한 상호작용에 의해 원자가 더이상 움직이지 않으려는 상태가 되고 각 위치간의 원자의 위상적 관계가 잘 정의되지 않는다(자발적으로 선택한다). 이를 모트 부도체 (Mott insulator) 상태라고 한다. 광격자의 세기를 조절하여 두 가지 상태 (초유체-모트 부도체)를 넘나 들 수 있고, 이 과정에서 온도가 아닌 상호작용에 의한 양자 요동이 중요하고 양자 상전이라고 부른다.

양자기체 현미경을 이용하여 촬영한 중성 보존 원자의 모트 부도체 상태. 왼쪽과 같이 총 원자의 수가 적당한 개수가 있을 때는 평균적으로 1개의 원자들이 각 격자 위치에 들어있는 것을 관찰할 수 있다. 원자 개수를 늘리게 되면 오른쪽 그림과 같이 깊은 곳부터 2개의 원자가 채워지기 시작하면서 wedding cake 이라고 불리는 구조를 관찰할 수 있다. 광접착(photoassociation)효과에 의해 원자가 짝수개 존재하는 경우 원자가 없는 것으로 촬영된다. (출처 KAIST)

페르미-허버드(Fermi-Hubbard) 모형

2차원 페르미-허버드 모델은 고온 초전도체의 이해에 핵심이 되는 모델로 여겨지고 있다. 단순한 모형에도 불구하고, 계산이 매우 어려운 것으로 알려져 있다. 양자 기체 현미경을 이용한 페르미-허버드 모델을 구현하고 미시적인 수준에서 관찰할 수 있다. 공간적인 상관함수(correlation function)들을 구해낼 수 있는 것이 대표적인 사례라고 할 수 있다.

인공 게이지 장 (Artificial gauge field)

중성 원자는 전하가 없어서, 자기장에 대해 로렌츠 힘을 받지 않는다. 대신 광격자를 깊게 만들어 양자 터널링을 억제하고, 라만 레이저를 인가하거나 광격자를 빠르게 변조할 경우, 원자들이 터널링을 하면서 특정 위상을 얻을 수 있게 되고, 이를 이용해 자기장이 전자에 인가하는 게이지 장에 해당하는 효과를 얻을 수 있다. 이를 활용해 위상 물리 등의 응용이 가능하다.

스핀 모형

이징 모델 (Ising model)

리드버그 원자 시스템이나 기울인 허버드 모형을 활용하면 이징 모델을 구현할 수 있다. 다음과 같은 횡으로 장이 걸린 이징 헤밀토니언을 구현할 수 있다.

\[H_{Ising} = J\sum_{\langle i,j\rangle}\hat{\sigma}^{z}_i \hat{\sigma}_j^{z} \sum_i h_x \hat{\sigma}^x_i + h_z \hat{\sigma}^z_i\]

$$J$$는 판데르발스 상호작용에 의해 생성되는 스핀 상호작용, $$\sigma$$는 파울리 연산자, $$h$$는 유효적인 공간적 방향의 자기장이다. $$h_x$$의 경우 인가한 레이저의 라비 진동수에 의해서 세기가 결정되고, $h_z$는 레이저의 디튜닝에 의해 결정된다.

하이젠베르그 (Heisenberg model)

쌍극자 모멘트를 가진 원자 및 분자나 스핀을 성분을 가진 허버드 모델의 superexchange 상호작용을 활용하면 다음과 같은 하이젠베르그 스핀 모델을 구현할 수 있다.

\[H_H = J\sum_{\langle i, j \rangle} \mathbf{S_i} \cdot \mathbf{S_j}\]

여기서 $$\mathbf{S} = (S_x, S_y, S_z)$$ 는 스핀 연산자이고, $$J$$는 상호작용 결합상수로, 허버드 모형을 이용할 경우 $$J = 4t^2/U$$와 같이 나타낼 수 있다. 여기서는 등방적인 하이젠베르그 모델을 표현했으나, 비등방적인 해밀토니언도 구현할 수 있다.

리드버그 원자 기반 양자 컴퓨팅

리드버그 양자 시뮬레이터 개념도.

리드버그 원자는 하나 이상의 전자가 매우 높은 주 양자수로 들떠 있는 상태의 원자를 말한다. 주 양자수가 매우 큰 에너지 상태이기 때문에 원자의 크기가 매우 크다. 주 양자수가 100인 리드버그 원자의 크기는 마이크로 미터 정도에 육박하게 된다. 리드버그 원자는 기저상태로 전이하는 확률이 작으며 자발 방출로 붕괴하는 시간은 밀리 초 정도이다.

리드버그 원자는 수소 원자와 비슷하게 기술할 수 있으며 양자 결손(quantum defect)이라고 부르는 상수만큼의 에너지 준위 차이를 갖게 된다. 이 양자 결손은 주 양자수와 각운동량 양자수에 따라 다르게 주어지며 내각 전자의 수가 큰 원자일수록 양자 결손의 값이 커진다.

리드버그 원자는 높은 에너지 준위의 분광학연구에서 시작되었으며 광-자기 포획(MOT)의 발달과 함께 양자 정보에 관련된 연구로 발전하게 되었다.

장치 구성 및 특징

광 자기 포획으로 포획, 냉각된 중성 원자를 자기장 포획 우물이나 광학적 포획 우물로 포획한 후 리드버그 원자를 생성한다. 리드버그 원자를 생성하기 위해 기저 준위의 전자를 들뜬 상태로 만들어야 한다. 이 경우 그 에너지 차이에 해당하는 레이저를 쏘아줄 수 있으나, 이 경우 주파수가 UV 파장이기 때문에 필요한 강한 세기의 레이저를 구하기가 쉽지 않다. 일반적으로는 이광자(two-photon) 흡수를 통해 리드버그 원자를 만들게 된다. 예를 들어 루비듐(Rb) 원자의 경우 도플러 냉각에 이용한 780 nm 레이저를 이용하여 5S_1/2 에서 5P_3/2 로 전이시킨 후 480 nm 레이저를 이용하여 5P_3/2 에서 97d_5/2 상태로 전이시켜 리드버그 원자를 생성할 수 있다

원리

원자 어레이 준비

리드버그 원자 실험 개요도.

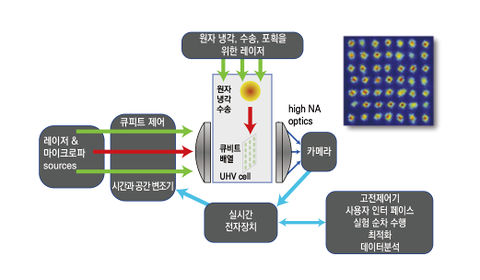
중성 원자의 경우 광격자를 이용하여 단일 원자 큐비트를 생성할 수 있는데, 리드버그 원자의 경우도 광격자를 이용하여 포획된 원자에서 선택적으로 큐비트를 생성하거나, 주변 원자와의 다양한 게이트 조작(Operation)을 이용하여 다양한 양자 시뮬레이션을 수행한다.

하나의 제어 원자로 주변의 타겟 원자 상태를 조작하는(CNOT)^k 게이트나 그 반대의 경우인 C_kNOT 게이트, 여러 개의 원자 사이의 리드버그 상태를 공유하는 양자 중첩(Entanglement)등을 구현할 수 있다.

리드버그 봉쇄(Blockade)

리드버그 원자의 강한 정전기 상호작용(electrostatic interaction)은 주변의 원자들에게 간섭 작용을 일으키면서 원자의 에너지 레벨을 변화시킨다. 리드버그 원자 주변의 원자는 에너지 레벨이 변경되었기 때문에 같은 전이 레이저에 대해 반응하지 않게 되며, 들뜬 상태로 전이가 되지 않게 된다. 즉, 리드버그 원자의 일정 거리 안에서는 다른 리드버그 원자가 생기지 않게 되는 것이다. 이를 excitation blockade 혹은 dipole blockade라 부르며 리드버그 원자를 양자 정보에 사용할 수 있는 기본 배경이 된다.

양자 게이트

리드버그 원자의 excitation blockade를 이용한 CNOT게이트 구현. a) 제어 원자가 $$|0>$$ 상태에 있을 경우 excitation laser의 파이 펄스에 의해 리드버그 상태가 되지 않으며 타겟 원자는 $$|1>$$ 과 $$|r>$$ 사이의 라비 진동을 관측할 수 있다. b) 제어 원자가 $$|1>$$ 상태에 있을 경우 원자는 리드버그 상태가 되므로 타겟 원자는 항상 기저 준위에 있게 된다.

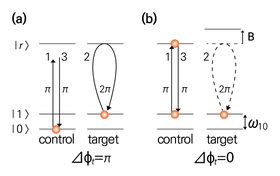
리드버그 원자에서만 볼 수 있는 excitation blockade를 이용하여 CNOT 게이트를 구현할 수 있다. 제어하는 중성 원자가 리드버그 상태인지에 따라 그 이웃 원자의 리드버그 상태를 조절할 수 있으므로 이를 이용하여 게이트를 구현하게 된다.

개발 현황

중성 원자 플랫폼은 이온 트랩과는 달리, 전하를 띠지 않는 중성 원자를 사용하여 양자 컴퓨팅을 구현한다. 각 원자들이 전하를 띠지 않기 때문에 원자들 간 상호작용이 약하다는 단점이 존재하지만, 반대로 이러한 특성 덕분에 대규모의 원자들을 광학 격자나 광집게를 사용하여 안정하게 포획할 수 있다. 이러한 장점으로 인하여 양자 다체계에서 나타나는 양자 상전이, 양자 홀 효과 등의 물성을 양자 시뮬레이션 할 수 있는 플랫폼으로서 기대되고 있다. 중성 원자의 경우 Pasqal 등의 기업이 본격적인 하드웨어 플랫폼 개발에 착수 중이며, 수많은 대학에서도 중성 원자를 이용한 양자 컴퓨팅 연구가 이루어지고 있다.

하드웨어 개발 현황

Pasqal에서 개발하고 있는 양자 시뮬레이터.

중성 원자 플랫폼의 경우 원자간 상호작용의 세기가 약해서 모든 원자간 연결성이 보장되지 못하다는 단점이 있다. 하지만 최근 리드버그 중성 원자를 활용하여 원자간 상호작용의 세기를 높여, 중성 원자를 양자 컴퓨팅 및 시뮬레이션 플랫폼으로서 활용하려는 시도들이 이루어지고 있다. 아직까지 이온 트랩만큼의 하드웨어 개발이 진행되지는 않았지만, 일부 기업들을 중심으로 하드웨어 개발이 꾸준히 진행 중이다. 대표적으로 Pasqal 등의 기업에서 현재 100개의 중성 원자 큐비트를 사용하는 양자 시뮬레이터의 개발이 이루어진 상태이다. 이러한 Pasqal의 중성 원자 플랫폼은 bosonic SSH model의 양자 시뮬레이션, Maximum Independent Set(MIS)의 최적화 문제를 푸는 등에 활용되고 있다.

Pasqal 등의 기업 이외에도, Harvard, Caltech 등의 대학에서도 중성 원자를 활용한 양자 컴퓨팅 및 시뮬레이션 하드웨어 플랫폼이 활발히 연구되고 있다. 대표적으로 2017년 Harvard 대학을 중심으로 51개의 리드버그 중성 원자 양자 시뮬레이터를 활용한 Ising-type 양자 스핀 모델에 대한 양자 시뮬레이션 연구가 이루어졌다. 또한 2018년 Harvard 대학과 Caltech을 중심으로 리드버그 중성 원자들을 활용한 얽힘 실험에서 97% 이상의 피델리티를 보이는 동시에 수십 us 정도의 결맞음 시간이 달성되기도 하였다.

다음은 리드버그 원자 어레이를 이용하여 양자컴퓨터 솔루션을 개발하고 있는 회사들이다.

• QuEra
• Atom-computing
• Pasqal
• Cold quanta