양자 소프트웨어 (Quantum Software)
<양자 기술백서 |
┗|양자컴퓨팅의 구현>
┗<양자 알고리듬 (Quantum Algorithm)|양자컴퓨팅 (Quantum Computing)>
양자 소프트웨어 스택 (Quantum Software Stack)
쇼어 알고리듬이 개발되면서 양자 컴퓨터가 가져올 컴퓨팅 성능 향상에 대한 관심과 기대가 높아졌지만 아직까지 그 이점과 한계에 대해 명확하게 알려진 바는 없다. 일반적으로 양자 컴퓨터가 특정 문제에 대해 좋은 성능을 보인다는 것이 증명되거나 예측되는 반면 모든 문제를 효율적으로 풀 수 있을 것으로 보이지는 않는다. 특히 고전 컴퓨터도 효율적으로 풀 수 있는 문제들에 대해서는 양자 이점(quantum advantage)이 없을 것으로 보인다.
양자 컴퓨터 개발에 소요되는 막대한 비용을 고려할 때, 양자 컴퓨터는 고전 컴퓨터를 완전히 대체하는 것이 아니라 특정 문제의 성능을 개선하기 위한 가속기(양자 가속기, quantum accelerator)의 형태로 사용될 것이다. 양자 가속기 모델 하에서 쉽고 단순한 논리 작업은 고전 컴퓨터를 통해 실행하면서 복잡하고 어려운 일부 작업의 성능을 양자 컴퓨터를 통해 개선시키는 것을 목표로 한다. 때문에 양자 컴퓨터는 수 십년에 걸쳐서 개발된 복잡한 고전 컴퓨터 프레임 워크와 매끄럽게 통합될 수 있어야 한다. 이 과정에는 양자 전송(quantum teleportation) 등 통신 기술과 보안 기술이 요구될 뿐만 아니라 양자 시스템을 위한 적절한 추상화를 제공하고 양자 하드웨어를 효율적으로 관리하기 위한 복잡한 소프트웨어 생태계(양자 소프트웨어 스택)를 필요로 한다.
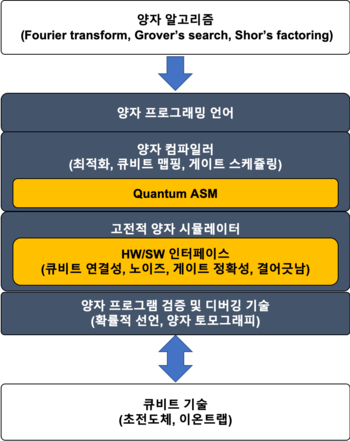
양자 소프트웨어 스택은 고전 컴퓨터 소프트웨어 스택과 통합되어야 하며, 이에 따라 둘은 유사한 형태를 띠게 될 것이다. 양자 컴퓨팅 기술도 이와 유사한 양자 소프트웨어 스택을 지니게 될 것으로 예측하는 것은 당연한 귀결이다. 현재 이러한 양자 소프트웨어 스택(그림 1) 기술을 개발하기 위한 연구가 Microsoft, IBM 등 세계적 IT 기업, Rigetti computing과 같은 스타트업 및 ETH Zurich과 같은 학계에서 활발하게 진행되고 있다.[1]
양자 소프트웨어 스택은 크게 양자 프로그래밍 언어, 양자 컴파일러, 고전 양자 시뮬레이션 (Classical Quantum Simulation)과 검증 및 디버깅 소프트웨어로 구성된다. 양자 프로그래밍 언어는 사용자에게는 적절한 추상화 수준을 제공하여 프로그래밍을 쉽게 하고 다양한 하드웨어로의 이식성(portability)을 확보하기 위한 기술이다. 양자 컴파일러는 주어진 양자 프로그램을 분석하고 보다 효율적인 프로그램으로 변환시켜야 한다. 이 과정에서 하드웨어가 지니는 자원 및 성능 제약 조건을 고려해야 한다. 이 과정에서 게이트 합성(gate synthesis), 큐비트 맵핑(qubit mapping), 게이트 스케쥴링(gate scheduling) 등의 기술이 필요하다. 소규모 양자 시스템을 시뮬레이션하고, 나아가 양자 컴퓨터 개발을 검증하고 디버깅 하기 위해서는 효율적인 고전 시뮬레이터가 필요하다. 특히, NISQ 시대의 양자 컴퓨터를 위해 큐비트 연결성(connectivity), 노이즈, 게이트 충실도(fidelity) 등 하드웨어 제약 사항을 고려하여 실제 구현될 양자 컴퓨터를 분석하기 위한 노이즈 시뮬레이션 기술도 필요하다. 그러나 고전 시뮬레이터는 지수적으로 증가하는 계산 및 공간 복잡도를 지녀 양자 시스템이 충분히 커지면 활용하기 어려울 것으로 보인다. 결국 확장이 용이한(scalable)한 양자 시스템 개발을 위해서는 다른 방식의 검증 및 디버깅 방법이 필요하다. 현재 확률적 선언(probabilistic assertion) 및 양자 토모그래피(quantum tomography) 등 양자 하드웨어를 검증하기 위한 여러 기술들이 개선 중에 있으나 여전히 효과적인 방법은 미비한 실정이다.
양자 소프트웨어 기술은 충분히 성숙되지 않아 기술 발전의 여지가 클 뿐만 아니라, 양자 컴퓨터 개발 과정에서 수반되는 여러 문제는 효율적인 소프트웨어를 통해서만 해결할 수 있다는 점에서 양자 컴퓨팅 기술 개발 전반에 커다란 영향을 미칠 것으로 전망된다.
양자 프로그래밍 언어 (Quantum Programming Language)
양자 프로그래밍 언어(quantum programming language)는 양자 알고리듬을 명세하고 양자 하드웨어를 다루기 위한 추상화(abstraction)를 제공한다. 추상화는 컴퓨터 공학을 관통하는 핵심 개념으로 불필요한 세부 사항을 감추고 핵심만 간추려 인터페이스로 정의하는 것이다. 사용자는 불필요한 하드웨어 특성에 신경 쓰지 않아도 되어 프로그래밍이 쉬워진다. 나아가 고 수준의 추상화는 한 번 작성된 프로그램을 여러 하드웨어에서 사용할 수 있도록 한다. 추상화는 하드웨어 개발자에게도 중요한 개념이다. 하드웨어 개발자는 응용 프로그램의 특성을 파악하고 중요한 기능만을 인터페이스로 정의한다. 미래 소자 기술이 발전해도 하드웨어 특성을 인터페이스에 반영하지 않았기 때문에 쉽게 적용할 수 있다. 여기서도 한 번 작성된 프로그램은 발전된 하드웨어에서 무리없이 작동한다.
한편, 프로그래밍 언어의 추상화 수준을 결정하는 것은 공학적 판단을 요한다. 일반적으로 프로그래밍 언어의 추상화 수준이 높을수록 프로그래밍하기 쉽고 다양한 하드웨어로의 이식성이 높아지는 반면 추상화 수준이 낮을수록 하드웨어의 특성을 이용하여 높은 성능의 프로그램을 작성하는 데 용이하다. 프로그래밍 언어 설계자는 언어의 사용 목적에 따라 하드웨어의 특성을 얼마나 드러낼 지 결정해야 하며, 양자 프로그래밍 언어를 위해 어떤 방식이 적합한지에 대한 일치된 견해는 없다. 사용자에게 높은 추상화 수준을 제공하면서도 하드웨어의 성능을 최대한 끌어내기 위해 프로그래밍 언어의 컴파일러를 통해 여러 단계의 변환을 거친다. 사용자는 기반 하드웨어의 특성, 성능 및 제약 조건들을 생각하지 않고도 프로그램을 작성할 수 있어야 하며, 컴파일러는 하드웨어의 특성을 충실히 반영해 효율적인 프로그램으로 변환하도록 해야 한다.
높은 추상화 수준을 지니고 있는 프로그래밍 언어를 고 수준 언어라 하며 낮은 추상화 수준을 지니고 있는 프로그래밍 언어를 저 수준 언어라 한다. 고 수준 언어의 설계 목표는 고전 컴퓨터를 위한 언어와 유연하게 통합되고 나아가 인간 사고 체계와 유사한 추상화를 제공하여 양자 역학 배경이 없는 사용자까지 포섭하는 것이다. Variational quantum eigensolver, Adiabatic computing 등 특정 문제에 적합한 모델이 있지만 일반적으로는 양자 회로(quantum circuit) 모델을 사용한다. 고 수준 언어는 함수형(functional) 언어와 명령형(imperative) 언어로 분류할 수 있다. 함수형 언어는 알고리듬을 (순수) 함수의 연쇄적 적용으로 표현하는 반면 명령형 언어는 주어진 양자 시스템에 일련의 게이트 연산을 적용하는 형식으로 표현한다. 일반적으로 함수형 언어는 복잡한 연산을 간략하게 표현할 수 있다는 장점이 있으며, 명령형 언어는 폰 노이만 아키텍처와 잘 대응되기 때문에 보다 직관적이다. 양자 프로그래밍 언어에 있어서 어떤 것이 더 적합한지에 대한 일치된 견해는 없다. 마이크로소프트에서 개발한 Q#은 함수형 언어, 프린스턴 대학 등에서 개발한 Scaffold는 명령형 언어의 예 (표 1)다.
저 수준 언어의 설계 목표는 하드웨어의 주요 특징들을 간추려내 추상화하는 것이다. 저 수준 언어는 중간 표현(IR, intermediate representation)이라고도 일컬어지는데 고 수준 언어와 하드웨어 ISA(instruction set architecture) 사이에 위치한다. 다양한 양자 컴퓨터는 분류 방식에 따라 공통된 특성을 지닐 수 있으며, 이러한 특성을 추상화하여 중간 표현을 설계한다. 중간 표현은 하나의 양자 컴퓨터뿐만 아니라 여러 개의 유사한 하드웨어 집합이 지니는 특성을 고려한 최적화를 가능하게 하여 불필요한 기능 중복을 없애는 데 핵심적인 역할을 한다. 중간 표현은 여러 단계에 걸쳐 있을 수 있다. 예컨대, 일반적인 양자 컴퓨터를 위한 중간 표현인 OpenQASM은 초전도체(superconducting) 양자 컴퓨터 혹은 이온 트랩(trapped-ion) 양자 컴퓨터를 위한 중간 표현으로 변환되고 최종적으로 목적 하드웨어의 ISA로 변환될 수 있다.
| 고 수준 언어 | 저 수준 언어 | 비고 | |
|---|---|---|---|
| 함수형 언어 | QWIRE[4] | 복잡한 연산을 표현하기에 적합. | |
| 명령형 언어 | 양자 시스템의 상태를 직관적으로 표현하기에 적합. | ||
| 비고 | 알고리듬을 기술하기에 적합. | 하드웨어의 특성을 반영하기에 적합. |
양자 컴파일러 (Quantum Compiler)
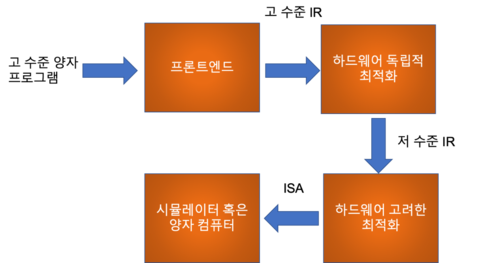
양자 프로그램은 여러 단계의 변화를 거치며 하드웨어에 적합하게 변환되는데 이 과정에서 양자 컴파일러의 역할이 매우 중요하다 (그림 2). 양자 컴파일러는 주어진 양자 회로를 하드웨어가 지니는 자원 및 성능상의 조건을 만족시키면서 가장 효율적인 프로그램의 형태로 변환하는 것이다. 나아가 NISQ시대의 양자 컴퓨터가 지니는 복잡한 자원 제약 조건 및 불안정성 문제는 컴파일러를 이용한 최적화 기술의 중요성이 더욱 주목된다.
양자 하드웨어는 큐비트 기술에 따라 사용할 수 있는 게이트의 종류, 동시에 실행될 수 있는 게이트의 수, 결어긋남(decoherence) 시간, 게이트 충실도, 양자 오류 정정 부호(quantum error correction code)의 종류, 물리적 큐비트의 연결성(connectivity) 및 개수 등 다양한 제약을 지니고 있다. 컴파일러는 각 하드웨어에 맞는 특성들을 반영하여 최종적으로 실제 하드웨어에서 동작할 수 있는 프로그램으로 변환해야 한다. 사용자는 고 수준 언어로 양자 프로그램을 작성한다. 일반적으로 양자 프로그램은 바로 실행 가능한 형태로 변환되는 것이 아니라, 중간 언어 표현으로 변환되어 필요한 최적화가 적용된 후 하드웨어 ISA 수준으로 변환하는 단계적 과정을 거친다.
각 단계에서는 잘 정의되어 있는 양자 프로그래밍 언어 혹은 중간 표현 간의 변환이 이루어진다. 단계를 내려갈수록 추상화 수준은 낮아지고 하드웨어의 특성은 드러난다. 이 때 컴파일러는 입력으로 받는 프로그램을 잘 분석한 뒤 같은 결과를 보이지만 보다 빠른 프로그램으로 변환한다. 나아가 컴파일러는 각 단계에서 드러난 하드웨어의 특성도 반영하여 프로그램 최적화를 수행해야 한다. 단계를 내려갈수록 하드웨어 독립적인 최적화보다 하드웨어를 고려한 최적화가 중요해진다. 이렇듯 중간 언어 표현도 여러 추상화 수준을 지닐 수 있으며 각 단계에서 요소 기술에 독립적인 최적화와 요소 기술을 고려한 최적화 기술이 적용된다.
고전 컴파일러와 달리 양자 컴파일러가 지니는 특징은 자원 제약의 엄격함이다. 특히, NISQ 시대의 양자 컴퓨터는 자원 제약이 심하고 노이즈에 민감하여 이를 모두 고려하면서도 성능이 뛰어난 프로그램으로 변환하는 것이 쉽지 않다. 여러 기술이 접목될 수 있지만 일반적으로 양자 컴파일러가 지원해야 할 기술은 게이트 합성(gate synthesis), 큐비트 맵핑(qubit mapping) 및 게이트 스케줄링(gate scheduling) 세 가지로 볼 수 있다.
게이트 합성은 임의의 게이트를 양자 하드웨어가 지원하는 게이트로 변환하는 기술이며, 일반적으로 양자 하드웨어는 소수의 범용(universal) 게이트 집합만을 지원하며 이를 원시 게이트(primitive gates)라 한다. 임의의 양자 게이트는 유한한 개수의 원시 게이트들만 사용하여 높은 정밀도로 근사할 수 있으나, 정밀도가 높아질수록 사용되는 게이트의 수가 증가하여 소모되는 자원 및 시간이 증가한다. 높은 정밀도는 프로그램 작성자의 의도에 부합하는 반면 긴 실행 시간이 필요하므로 상충 관계에 있다. 특히, 근사 해야 할 게이트가 많을 경우 정밀도를 충분히 높도록 설정하여 근사로 인한 오류가 증폭되는 것을 방지할 필요가 있다. 컴파일러는 양자 회로를 분석하여 근사 오류로 인한 영향을 미미하게 하면서 높은 수준의 정밀도를 확보하기 위한 게이트 근사 기술이 필요한다.
큐비트 맵핑은 양자 회로에서 사용되는 논리적 큐비트들을 실제 하드웨어 상의 물리적 큐비트에 대응시키는 기술이다. 일반적으로 양자 오류 정정 부호 기술을 사용하기 위해 여러 개의 물리적 큐비트가 하나의 논리적 큐비트에 대응되도록 설계된다. 그 밖에도 물리적 큐비트들간의 연결성 및 고전 레지스터와의 통신 채널 등의 제약으로 인해 큐비트 간의 자리를 바꾸든지 양자 전송 연산을 해야 할 경우가 발생할 수 있다. 양자 컴파일러는 임의의 고 수준 양자 회로를 원시 게이트와 물리적 큐비트로 구성된 동일한 연산을 수행하는 회로로 변환해야 한다.
게이트 스케쥴링은 게이트 합성을 통해 변환된 원시 게이트들의 적용 순서를 효율적으로 결정하는 기술이다. 제어 신호의 전송 시간 및 간섭 현상, 동시에 사용될 수 있는 게이트 연산의 종류, 결어긋남(decoherence) 및 교정(calibration) 시간 등의 제약으로 인해 같은 양자 회로에 대해서도 게이트 연산의 적용 순서에 따라 성능상의 차이를 보인다. 양자 컴파일러는 양자 회로에 기술된 게이트들간의 의존성을 파악하고 이를 위배하지 않으면서 하드웨어의 성능을 끌어올리기 위한 최적화 기술을 지니고 있어야 한다.
고전 양자 시뮬레이션 (Classical Quantum Simulation)
하드웨어 개발에 있어서 시뮬레이션은 설계 변경의 유연성을 확보하고 하드웨어를 검증하기 위한 핵심 요소이다. 고전 컴퓨터는 기 개발된 고전 컴퓨터를 사용하여 복잡한 시뮬레이션 과정을 거쳐 성능을 분석하고 개선하는 피드백의 과정을 거쳐 빠르게 성장할 수 있었다. 적어도 가까운 미래에는 양자 컴퓨터도 마찬가지의 과정을 거쳐 개발될 것은 자명하다. NISQ 시대의 양자 컴퓨터가 지니는 불안정성에 비추어볼 때 시스템 검증의 역할을 할 고전 시뮬레이션 기술은 더욱 중요한 의미를 지니며, 더불어 고전 양자 시뮬레이터는 노이즈를 고려한 시뮬레이션도 지원해야 한다. 나아가 양자 시스템을 효율적으로 시뮬레이션하는 것은 현대 과학 계산 분야에서도 매우 중요하다. 고전 양자 시뮬레이터는 임의의 양자 컴퓨터를 추상화하는 가상 양자 컴퓨터로 볼 수 있으며, 양자 컴퓨터 개발의 속도를 높이고 양자 컴퓨팅 생태계를 확장하기 위해서는 효율적인 고전 양자 시뮬레이션 기술이 절실하다.
고전 컴퓨터를 통한 효율적인 양자 시스템 시뮬레이션 알고리듬이 존재하는지에 대해서는 알려진 바가 없다. 현재 사용되는 무차별 대입(brute-force) 시뮬레이션 방법은 지수적으로 증가하는 공간 및 시간 복잡도를 지닌다는 점에서 한계가 있다. 현재 세계 최고 성능의 슈퍼 컴퓨터를 이용한 고전 시뮬레이션의 크기는 50큐비트 전후의 시스템에 머물고 있다. 당연하게도 노이즈를 고려한 시뮬레이션은 메모리 사용량과 실행 시간이 증가한다. 이를 극복하기 위한 연구가 진행되고 있지만 중요한 돌파구는 찾아지지 않고 있다. 다만 가용한 고전 컴퓨팅 자원의 효율을 높이거나, 특정 조건하에서의 양자 시스템에 대한 시뮬레이션 성능을 높이는 두 가지 방향에서 연구가 진행되고 있다.
대규모 클러스터를 사용하여 고전 컴퓨팅의 성능을 극한으로 올리면 시뮬레이션 가능한 양자 프로그램의 크기가 커진다. 특히 양자 회로 시뮬레이션은 쉽게 병렬 처리할 수 있기 때문에(embarrassingly parallel) 대규모 클러스터 상에서 병렬 처리하여 부족한 연산 자원 및 메모리 자원을 확보하여 실제 실행 시간을 줄이고 보다 큰 시스템을 시뮬레이션 할 수 있다. 그러나 시뮬레이션 알고리듬의 복잡도가 개선되는 것은 아니기 때문에 확장성(scalability)에 한계가 있다. 현재 50 큐비트 전후가 그 한계점으로 전망되고 있으나, 컴퓨팅 기술의 발전 속도에 따라 더 증가할 수 있을 것으로 보인다.[8]
클러스터를 이용한 시뮬레이션 성능의 병목 지점은 노드 간의 통신에 있다. 게이트가 적용되는 위치에 따라 매 게이트 연산마다 통신이 발생할 수 있기 때문이다. 대부분의 클러스터 시뮬레이션 기술은 이러한 통신 병목을 해소하는 것을 목표로 한다.[9][10] 대표적으로 IBM은 양자 회로를 텐서 네트워크(tensor network)로 표현하고 텐서 축소(tensor contraction) 연산을 이용해 부분 회로로 분할하여 하나의 노드 안에서 통신 없이 시뮬레이션 할 수 있는 크기로 줄인다.[10] 부분 회로에 대한 시뮬레이션 결과를 마친 노드들은 최종적으로 양자 얽힘을 표현하기 위하여 통신을 통해 다시 정규화된 상태로 연산을 이어나간다. 텐서 네트워크 표현은 일반적으로 사용될 수 있지만 양자 회로 분할을 통해 클러스터 상에서 불필요한 통신을 줄이는 데 중요한 기술이다.
임의의 양자 프로그램을 시뮬레이션하는 것이 아닌 특정 조건을 만족시키는 프로그램의 경우 보다 효율적인 시뮬레이션 알고리듬을 사용할 수 있다.[11][12] 대표적으로는 클리포드(Clifford) 게이트 집합으로 구성된 이른바 “stabilizer” 회로에 대한 다항 시간 시뮬레이션 알고리듬 기술이 개발되어 있다.[11] 클리포드 게이트 집합은 범용 게이트 집합은 아니라는 점에서 한계가 있지만, Shor 오류 정정 부호 등 특정 양자 오류 정정 부호의 경우 클리포드 게이트 집합으로만 구성할 수 있다는 점에 착안하여 대규모 QECC(quantum error correcting code) 연구에 활용된다.
양자 얽힘의 정도 낮은 회로에 대해서도 효율적인 시뮬레이션 알고리듬이 개발되었다. 양자 얽힘의 정도가 낮은 경우 슈미트 분해(Schmidt decomposition)를 이용하여 시스템의 상태를 행렬 곱 상태(Matrix product state, MPS)로 표현하면 불필요한 연산 및 공간을 줄여서 효율적으로 시뮬레이션 할 수 있다.[12] 이외에도 MPS는 양자 시스템을 기술하기 위한 새로운 형식(formalism)으로 대두되고 있다.
| 무제약 시뮬레이션 | 제약적 시뮬레이션 | ||
|---|---|---|---|
| 대규모 클러스터 사용 | Stabilizer 회로 | Matrix product state | |
| 성능 | 가용한 노드의 개수에 비례함 | 다항 시간 | 다항 시간 |
| 비고 | 확장성을 갖지 않음 | 사용할 수 있는 게이트 집합이 제약되어 있음 | 양자 얽힘의 정도가 낮아야 함 |
검증 및 디버깅
복잡한 프로그램 및 시스템을 개발하는 핵심 기술 중 하나는 검증 및 디버깅 기술이다. 고전 컴퓨팅 기술은 복잡한 시스템을 간단하게 모델링할 수 있는 인터페이스와 고성능 시뮬레이터를 통해 개발 비용을 줄이고 개발 속도를 개선시켜왔다. 고전 컴퓨터의 결정적 계산 모델은 사용자가 프로그램을 쉽게 검증하고 개발할 수 있도록 하였다. 대규모 양자 시스템을 개발하기 위해서도 이러한 효과적인 검증 및 디버깅 기술이 절실하다. 그러나 현재 기술로는 매우 어려운 일이 될 것으로 예측된다.
이러한 어려움은 크게 두 가지 원인에서 기인한다. 첫째, 양자 시스템은 큐비트의 개수에 지수적으로 비례하는 상태 공간 크기를 가지며 결국 대규모 양자 프로그램을 검증하는 것은 사실상 불가능하다. 따라서 대규모 양자 컴퓨터 개발은 복잡한 시스템을 단순하게 기술하기 위한 해석적 모델링 기술이 필요로 한다. 둘째, 양자 붕괴(collapse) 현상으로 인하여 사용자는 시스템의 최종적인 상태가 아닌 측정을 통해 일부 표본만 얻을 수 있다. 사용자는 자신이 기술한 알고리듬이 목적한 최종 상태에 놓이게 되었는지 확인하기 매우 어렵다. 나아가 양자 붕괴 현상은 작성된 양자 프로그램을 디버깅하는 것을 어렵게 만들 뿐만 아니라 시스템 오류의 원인을 분석하고 개선하는 것을 어렵게 만든다. 특히 NISQ 시대의 양자 컴퓨터가 지니는 오류 취약성은 문제를 더욱 복잡하게 만든다.
현재 단계에서 적용되고 있는 양자 프로그램 검증 및 디버깅 기술을 실행 중 검증과 실행 후 검증 크게 두 가지로 나눌 수 있다. 실행 중 검증은 실행 중간에 양자 프로그램이 만족시켜야 할 특성을 사용자가 명세하고 이를 프로그램에 선언(assertion)의 형태로 표현하는 것이다.[13] 선언은 고전 컴퓨터에서 효과적으로 사용되는 기술로 사용자가 목적한 바를 논리적 선언의 형태로 기술하고 시스템이 이에 따라 변화하고 있다는 것을 실행 중간에 검사하여 확인하는 것이다. 만약 명시된 특성이 만족되지 않으면, 프로그램은 오류를 출력하고 종료한다. 양자 프로그램의 선언도 이와 유사하다. 단, 양자 프로그램의 특성상 참과 거짓으로 구별되는 논리적 선언과 달리 확률적 선언의 형태를 지니게 된다. 실제 양자 하드웨어 상에서 확률적 선언을 실행하기 위해서는 보조 큐비트(ancillary qubit)를 필요로 한다. 우선 보조 큐비트와 사용되는 큐비트가 양자 얽힘 상태에 놓여있도록 한다. 확률적 선언의 실행은 보조 큐비트에 대한 측정을 통해 이루어지며, 검증이 끝난 뒤에는 다시 양자 얽힘 상태를 만들도록 해야한다. 이 모든 과정은 컴파일러에 의해 자동으로 수행될 수 있다.
실행 후 검증은 동일한 양자 프로그램을 반복적으로 실행하여 얻은 결과를 통해 측정 전 상태에 대한 통계적 추론을 하는 것이다 (quantum tomography). 이 때 통계적으로 유의미한 결과를 얻기 위해 반복해야 할 실험의 수는 큐비트의 개수에 지수적으로 비례한다는 것이 알려져 있다. 결국 고전 시뮬레이션을 수행하는 것과 다르지 않은 시간이 소모되며, 양자 이점을 포기해야 한다. 실행 후 검증 기술의 핵심은 적은 반복 만으로 주어진 양자 프로그램이 생성할 확률 분포를 추론하는 것이다. 특히 NISQ 시대의 양자 컴퓨터 상에서 적은 횟수의 실험 만으로 결과를 보장할 수 있다면 상당한 성능 향상을 끌어낼 수 있을 것으로 예측된다. 물론 실행 후 검증의 경우 오류의 발생 지점과 원인을 파악하기 어렵다는 한계가 있다는 점에 주의해야 한다.
참고 문헌
- ↑ Microsoft: https://www.microsoft.com/en-us/quantum; Rigetti computing: https://www.rigetti.com; ETH 대학 Project Q: https://projectq.ch; IBM: https://qiskit.org
- ↑ https://docs.microsoft.com/ko-kr/quantum/language/?view=qsharp-preview
- ↑ Green, A. S., Lumsdaine, P. L., Ross, N. J., Selinger, P., & Valiron, B. (2013, June), “Quipper: a scalable quantum programming language”, In ACM SIGPLAN Notices , 48)(6) : 333, ACM.
- ↑ Paykin, J., Rand, R., & Zdancewic, S. (2017, January), “QWIRE: a core language for quantum circuits”, In ACM SIGPLAN Notices, 52(1) :846, ACM.
- ↑ Selinger, P. (2004), “Towards a quantum programming language”, Mathematical Structures in Computer Science, 14(4) : 527.
- ↑ Abhari, A. J., Faruque, A., Dousti, M. J., Svec, L., Catu, O., Chakrabati, A., ... & Chong, F. (2012), Scaffold: Quantum Programming Language, PRINCETON UNIV NJ DEPT OF COMPUTER SCIENCE.
- ↑ 7.0 7.1 McKay, D. C., Alexander, T., Bello, L., Biercuk, M. J., Bishop, L., Chen, J., ... & Gomez, J. (2018), “Qiskit backend specifications for OpenQASM and OpenPulse experiments”, arXiv preprint arXiv:1809.03452.
- ↑ Pednault, E., Gunnels, J. A., Nannicini, G., Horesh, L., & Wisnieff, R. (2019), “Leveraging secondary storage to simulate deep 54-qubit sycamore circuits”, arXiv preprint arXiv:1910.09534.
- ↑ Markov, I. L., & Shi, Y. (2008), “Simulating quantum computation by contracting tensor networks”, SIAM Journal on Computing, 38(3) : 963.
- ↑ 10.0 10.1 Pednault, E., Gunnels, J. A., Nannicini, G., Horesh, L., Magerlein, T., Solomonik, E., ... & Wisnieff, R. (2017), “Breaking the 49-qubit barrier in the simulation of quantum circuits”, arXiv preprint arXiv:1710.05867.
- ↑ 11.0 11.1 Aaronson, S., & Gottesman, D. (2004), “Improved simulation of stabilizer circuits”, Physical Review A, 70(5) : 052328.
- ↑ 12.0 12.1 Perez-Garcia, D., Verstraete, F., Wolf, M. M., & Cirac, J. I. (2006), “Matrix product state representations”, arXiv preprint quant-ph/0608197.
- ↑ Huang, Y., & Martonosi, M. (2019, June), “Statistical assertions for validating patterns and finding bugs in quantum programs”, In Proceedings of the 46th International Symposium on Computer Architecture : 541, ACM.