이온 트랩 (Ion Trap)
<양자 기술백서 |
개요
이온 트랩을 이용한 양자 컴퓨팅
Radio Frequency(RF) Paul 트랩은 1980년대부터 이온 트랩에 사용되어 왔는데, 긴 트랩 시간, 트랩 이온의 양자 상태의 긴 결맞음 시간과 함께 이온 간 강한 쿨롱 상호작용이 가능하고, 레이저를 이용한 광학적인 방법으로 개개의 이온의 양자 상태를 조작하고 측정할 수 있다는 장점이 있어 지금까지 이온 트랩에 많이 사용되어 왔다. 1995년, Cirac과 Zoller는 트랩된 이온의 양자 상태와 이온들간의 양자화된 운동(motional) 상태를 결합시켜 CNOT 게이트를 구현했는데(Cirac, Zoller, 1995)[1] 이후로 CNOT 게이트뿐만 아니라 이온들의 양자 얽힘을 만드는 다양한 양자 게이트들이 트랩된 이온들의 양자 상태와 운동 상태를 결합시키는 방식으로 구현되었다.
현재 이온 트랩은 큰 스케일의 양자 컴퓨터를 구현하기 위한 가장 촉망받는 기술 중 하나이다. 이온 트랩 이용한 단일 큐비트 게이트 구현, 두 개의 큐비트 게이트 구현, 큐비트 상태 초기화, 큐비트 상태 측정은 양자오류정정 부호를 사용할 수 있을 만큼 높은 양자 신뢰도로 가능하지만 실용적으로 사용하기 위해서 큐비트 수를 늘리면서도 컴퓨팅의 높은 신뢰도를 유지하는 연구가 필요하다 (Bruzewicz et al., 2019).[2]
이온 트랩의 큐비트의 종류
이온 트랩을 이용한 큐비트는 크게 하이퍼파인(hyperfine) 큐비트, 지만(Zeeman) 큐비트, 파인 구조(fine structure) 큐비트, 광학(optical) 큐비트 네 종류로 나눌 수 있다 (Bruzewicz et al., 2019).[5]
하이퍼파인 구조(hyperfine structure)는 원자에서 핵의 궤도를 돌고 있는 전자의 자기쌍극자(전자 스핀)과 전자의 각운동량사이의 방향 차이에서 발생한 파인 구조에 핵자의 자기쌍극자(핵 스핀)의 방향 차이까지 고려한 미세한 에너지의 차이로 인해서 생긴다.[6] 하이퍼파인 구조의 에너지 레벨은 외부 자기장의 변동에 1차 근사로 무관하기 때문에, 1~1000 초 정도의 상대적으로 긴 양자 결맞음 시간을 가진다 (NASEM, 2019).[7] 하이퍼파인 큐비트는 이온의 하이퍼파인 상태들을 큐비트 상태로 사용하고 상태 간 에너지 차이는 GHz(기가헤르츠) 단위의 마이크로파 영역이어서 마이크로파를 이용한 에너지 상태의 전이가 가능하다. 마이크로파를 아주 작게 포커스를 할 수는 없어서 트랩된 각각의 이온의 상태를 전이시키기 위해서는 두 하이퍼파인 상태의 에너지 차이에 해당하는 주파수만큼 차이가 나는 레이저 두 개를 이용해 라만 전이를 할 수 있다.
지만 효과(Zeeman effect)는 원자가 외부 자기장에 놓여있을 때 에너지 레벨이 분리되는 현상이다. 보통 에너지 레벨의 차이는 MHz 단위이다. 지만 큐비트는 지만 효과로 분리된 에너지 레벨들을 큐비트로 사용한다. Zeeman 큐비트의 에너지 레벨은 외부 자기장의 세기에 의존하기 때문에 자기장의 변동이 양자 결맞음 시간을 줄이거나, 양자 게이트의 연산 에러를 만들 수 있는 문제가 있지만, 자기장의 세기가 안정화되었다면 계산의 에러가 하이퍼파인 큐비트에 비해서도 작을 수 있다 (Brown, 2018).[8]
미세 구조는 비상대론적 슈뢰딩거 방정식에 상대론적 효과를 보정해주는 효과와 spin-orbit 커플링에 의한 에너지 분리이다. 스핀-궤도 커플링은 전자의 궤도 운동에 의한 자기장과 전자의 자기 모멘트인 스핀의 상호작용으로 생긴다 (Griffiths, 2018).[9] 미세 구조 큐비트는 미세 구조 레벨을 큐비트로 사용하고 에너지 레벨의 차이는 THz 단위이다 (Bruzewicz, 2019).[10]
광학 큐비트는 이온의 바닥 상태와 준안정 들뜬 상태를 사용한다. 두 상태의 에너지 차이는 수백 THz 단위로 빨간색 광학 레이저의 에너지 차이와 같다. 광학 큐비트는 99.9 퍼센트 보다 높은 효율로 준비와 측정이 가능하고 결맞음 시간은 1~30 초의 단위이다 (NASEM, 2019).[11]
이온 트랩의 장단점
이온 트랩을 이용한 이온 큐비트가 다른 종류의 큐비트에 비해 갖는 장점은 결맞음 시간이 길다는 것이다. 하이퍼파인 큐비트는 스핀-에코나 다른 동적인 디커플링 없이도 50초 정도의 결맞음 시간을 갖고, 동적인 디커플링을 이용하면 600초의 결맞음 시간이 가능하다. 두 개의 큐비트 게이트 시간이 일반적으로 1에서 100 $$\mu s$$ 임을 생각하면 결맞음 시간과 게이트 시간의 비율은 $$\sim 10^{6}$$ 정도로 초전도 큐비트(~$$10^{3}$$), 리드버그 원자 큐비트(~$$10^{2}$$)에 비해서 크다.
또 다른 장점은 단일 큐비트 게이트와 두 개의 큐비트 게이트가 아주 높은 신뢰도로 구현될 수 있다는 점이다. 단일 큐비트 게이트의 신뢰도는 99.9999% 이상으로 도달하였고, 2-큐비트 얽힘 게이트의 신뢰도는 하이퍼파인 큐비트의 경우 99.9%에 도달하였고, 광학 큐비트의 경우 99.6%에 도달하였다. 이 정도의 신뢰도는 현재 초전도체 큐비트만 도달하였다.
상태의 초기화와 측정 또한 신뢰도가 높다. 200 $$\mu s$$ 보다 적은 측정 시간일 경우 99.99% 이상의 신뢰도에 도달하였고, 11 $$\mu s$$ 보다 적은 측정 시간일 경우 99.93%의 신뢰도에 도달하였다. 또한, 상태의 초기화와 측정을 한 번에 하는 경우 신뢰도는 99.93%의 신뢰도에 도달하였다. 또 다른 장점은 트랩된 이온들은 양자상태의 구조 및 큐비트의 주파수가 동일하기 때문에 이온을 큐비트로 사용할 경우 시스템의 안정성이 높고, 양자게이트의 조작이 상대적으로 용이하다.
단점으로는 게이트 시간 자체가 길다는 점이 있다. 높은 신뢰도의 두 개의 큐비트 게이트는 이온 트랩으로 수 십 $$\mu s$$에 구현이 되었는데, 초전도체 큐비트의 경우 수 십$$ns$$에 가능하다. 이러한 상대적으로 느린 양자연산속도는 이온 트랩을 이용한 양자컴퓨팅 구현에 어려움들중의 하나로 생각되고 있다. 초단파 펄스를 이용하거나 pulse shaping을 이용해 게이트 시간을 줄이는 연구가 있었지만 2~20 $$\mu s$$ 사이의 시간으로만 줄이는 경우에도 양자 신뢰도가 76%에 불과하다. 또 다른 단점으로는 다른 플랫폼과 마찬가지로 큐비트의 개수를 100개 이상의 스케일로 늘리는데 여러가지 물리적인 한계점이 존재한다는 것이다 (Bruzewicz, 2019).[10]
구현 방법
트랩 장치의 구조
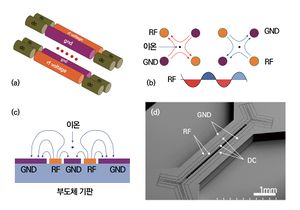
시간에 따라 변하는 전자기장을 이용하면 이온을 공간상에 포획할 수 있다. 이는 전기장과 자기장을 동시에 이용하는 Penning 트랩과 전기장만을 이용한 Paul 트랩의 두 가지 종류가 있다. 대부분의 이온 트랩 컴퓨팅 시스템은 Paul 트랩을 사용한다. Paul 트랩에서는 두 개의 전극에 RF 전압이, 또 다른 두 개의 전극에 접지(ground) 전압이 걸린다. 여기에서, RF 전기장의 시간에 따른 평균값인 유사 퍼텐셜(pseudo potential)이 형성되며, 이 RF 전기장이 최소가 되는 공간상의 지점에서 이온이 포획된다. 이 RF전압은 실린더 형태의 포텐셜을 구성하며, 추가적으로 DC 전압을 인가함으로써 3차원 공간의 한 지점에 이온들을 포획하게 된다. 전통적으로 이러한 트랩 구조물은 그림 3 (a), (b)에서처럼 트랩에 사용되는 금속 및 구성요소들을 가공한 뒤, 손으로 조립하는 과정을 거쳤지만, 요즘에는 기존 컴퓨터 하드웨어처럼 반도체 공정을 이용해 만드는 경우가 많다. 공정 기술의 도입은 더 복잡한 트랩 구조를 가능하게 만들고, 트랩된 이온들을 움직이는 이온 셔틀링을 가능하게 했고, 또한 시스템에서 사용하는 큐비트의 수를 늘릴 수 있게 만들었다. 그림 3 (c), (d)는 반도체 공정을 통해 만든 Paul 트랩의 예시이다 (NASEM, 2019).[13]
하이퍼파인 이온 큐비트의 초기화
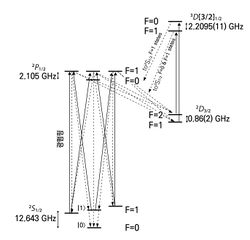
그림 2.4‑4 은 171Yb+ 이온의 하이퍼파인 구조를 큐비트로 사용하는 경우 이온의 초기화 과정을 나타낸다. 그림에서처럼 하이퍼파인 구조의 2$$S_{1/2}$$|F=0, mf=0⟩, 2$$S_{1/2}$$|F=1, mf=0⟩ 두 상태를 큐비트의 |0⟩, |1⟩ 상태로 사용한다. 상태를 초기화 하는 것은 큐비트의 상태를 |0⟩ 상태로 만드는 것을 의미한다. 2$$S_{1/2}$$|F=1⟩ 상태와 2$$P_{1/2}$$|F=1⟩ 상태 사이의 공진 주파수의 레이저를 이용해 |1⟩ 상태를 2$$P_{1/2}$$|F=1⟩ 상태로 전이시키면 1/3의 확률로 |0⟩ 상태로 떨어지고, 나머지는 2$$D_{3/2}$$|F=1⟩, 2$$D_{3/2}$$|F=2⟩로 떨어진다. 다른 주파수의 레이저를 이용해 이 상태를 2$${D\lbrack 3/2\rbrack}_{1/2}$$|F=1⟩, 2$${D\lbrack 3/2\rbrack}_{1/2}$$|F=0⟩ 상태로 전이시키면 다시 |0⟩ 또는 |1⟩ 상태로 떨어지게 된다. 초기의 큐비트 상태가 |0⟩과 |1⟩의 중첩 상태일 경우 이 과정을 반복하면 |0⟩ 상태는 그대로 |0⟩ 상태로 유지되고 |1⟩ 상태는 일정한 확률 이상으로 |0⟩ 상태로 떨어져 결국 |0⟩ 상태만 남게 된다 (Olmshenck et al., 2007).[15]
하이퍼파인 이온 큐비트의 양자 게이트
-
그림 5 ‑ 단일 큐비트를 표현하는 Bloch sphere(Debnath, 2016).[16]
-
그림 6 ‑ 171Yb+ 이온의 하이퍼파인 큐비트 사이의 Rabi oscillation을 측정한 결과(Olmschenk, 2007).[17]
단일 큐비트의 상태는 |0⟩ 상태와 |1⟩ 상태의 임의의 중첩으로 그림 5 에서처럼 블로흐 구(Bloch sphere) 위의 한 점으로 나타낼 수 있다. 단일 큐비트 게이트는 블로흐 구 위의 한 점을 다른 점으로 회전시키는 게이트이다. 이러한 게이트는 |0⟩ 상태와 |1⟩ 상태의 에너지 차이에 해당하는 주파수의 마이크로파(microwave)를 이용한 자기 쌍극자 전이 또는 |0⟩ 상태와 |1⟩ 상태의 에너지 차이에 해당하는 주파수만큼 주파수 차이가 나는 두 레이저를 유도 라만 전이(stimulated Raman transition)를 이용해 구현이 된다.[18] 그림 6은 마이크로파를 이용한 171Yb+ 이온의 하이퍼파인 큐비트 사이의 라비 진동(Rabi oscillation)을 측정한 결과이다. 마이크로파를 이용한 게이트는 12$$\mu s$$의 게이트 시간에 99.9999%의 신뢰도로 구현되었고, Raman 전이를 이용한 게이트는 7.5$$\mu s$$의 게이트 시간에 99.993% 신뢰도로 구현되었다 (Bruzewicz, 2019).[10]
2-큐비트 양자 게이트는 이온들의 양자상태(큐비트)들을 서로 공유하고 있는 양자운동을 이용하여 양자얽힘을 만든다. 두 이온 간의 얽힘 게이트는 Cirac과 Zoller에 의해 처음 제안되었고 그 이후로 양자 정보를 전달하기 위해 이온들이 공유하는 운동 모드(motional mode)를 이용한다는 같은 방식으로 여러 종류의 게이트들이 제안되었다 (Bruzewicz, 2019).[10]
두 이온이 전기장에 트랩된 경우 이온들은 서로 가까워지도록 하는 외부의 힘과 서로 멀어지도록 하는 두 이온 사이의 쿨롱 힘이 평형을 이루는 거리에 위치한다. 이 때 이온 사이의 거리가 가까워지면 쿨롱 힘이 강해져 이온 사이의 간격을 멀어지게 하고, 이온 사이의 거리가 멀어지면 쿨롱 힘이 약해져 이온 사이의 간격을 가까워지게 해 결국 이온이 공간 상에서 진동하게 된다. 두 이온의 진동은 서로 같은 방향으로 진동하는 모드와 서로 다른 방향으로 진동하는 모드 두 모드의 독립적인 조화 진동자(harmonic oscillator)로 설명이 된다. Cirac-Zoller 게이트는 이 중 한 모드를 이용해 우선 큐비트의 상태를 |↓⟩과 |↑⟩으로 나타낼 때, 그림 7과 같은 상태의 전이를 만든다.
-
그림 7 ‑ Cirac-Zoller 게이트의 전이(Lee et al., 2005).[19]
-
그림 8 ‑ Cirac-Zoller 게이트의 모식도(Lee et al., 2005).[20]
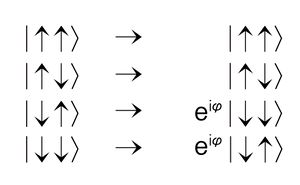
그림 8은 Cirac-Zoller 게이트의 모식도이다. 우선 두 이온은 진동의 최소 모드인 |n=0⟩ 상태로 준비된 상태에서 각각의 큐비트 상태를 가지고 있다. i)에서 청색 사이드밴드(blue sideband) 주파수를 이용해 첫 번째 큐비트의 |↓, n=0⟩ 상태만 |↑, n=1⟩ 상태로 전이시키면, 두 이온은 진동 모드를 공유하기 때문에 주파수에 반응을 한 경우 두 번째 큐비트도 |n=1⟩ 상태가 된다. ii)에서 |↓, n=1⟩ 상태만 반응하는 주파수로 두 번째 큐비트 상태의 위상을 $$\pi$$만큼 바꾸어 주고, iii)에서 다시 |↑, n=1⟩ 상태만 |↓, n=0⟩ 상태로 바꾸어 주면 진동 모드는 처음과 마찬가지로 |n=0⟩ 상태가 되고, 큐비트의 |↓↓⟩ 상태만 추가적인 $${e^i \pi}=-1$$ 의 위상을 얻는 Cirac-Zoller 게이트가 구현된다.
Cirac-Zoller 게이트와 단일 큐비트 게이트를 이용하면 그림 9 와 같은 CNOT 게이트를 구현할 수 있다 (Lee et al., 2005).[22]
Cirac-Zoller 게이트는 아무리 초기에 진동 모드를 |n=0⟩ 상태로 만들더라도 이온들이 외부의 전자기장으로부터 열을 얻을 수 있어 실용적으로 사용하기 힘들다. 1999년 M$$\varnothing$$lmer와 S$$\varnothing$$rensen이 큐비트 상태에 따라 다르게 작용하는 힘을 이용해 진동의 최소 모드를 이용할 필요가 없는 게이트를 제안하였다. M$$\varnothing$$lmer-S$$\varnothing$$rensen 게이트를 이용한 하이퍼파인 큐비트를 사용하는 두 개의 큐비트 게이트가 30 $$\text{μs}$$의 게이트 시간에 99.91%의 신뢰도로 가장 높은 신뢰도로 구현이 되었다 (Bruzewicz, 2019).[10]
하이퍼파인 이온 큐비트 상태의 측정
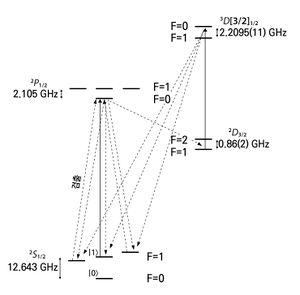
큐비트 상태의 측정은 상태에 따라 반응하는 공명형광(Fluorescence)을 이용한다. 측정을 할 큐비트 상태는 밝은 상태가 되어서 많은 수의 광자를 산란하거나, 어두운 상태가 되어서 거의 광자를 산란하지 않는다. 산란된 광자는 높은 개구수(numerical aperture)의 렌즈를 통해 모아져서 PMT(PhotonMultiplier Tube)나 CCD(Charge-Coupled Device) 카메라와 같은 검출기를 통해 검출한다 (Bruzewicz, 2019).[10]
그림 10은 171Yb+ 이온의 측정 과정을 보여준다. 2$$S_{1/2}$$|F=1⟩ 상태와 2$$P_{1/2}$$|F=0⟩ 상태 사이의 공진 주파수와 2$$D_{3/2}$$|F=1⟩ 상태와 2$${D\lbrack 3/2\rbrack}_{1/2}$$|F=0⟩ 상태 사이의 공진 주파수를 이용하면 |0⟩ 상태의 큐비트는 반응하지 않고 |1⟩ 상태의 큐비트는 지속적인 전이를 통해 |1⟩ 상태로 돌아오며 광자를 방출한다 (Olmshenck et al., 2007).[24]
4개의 이온을 트랩해서 EMCCD(Electron-Multipying Charge-Coupled Device)를 이용해 측정해 99.99%의 신뢰도에 도달하기도 하였다 (Bruzewicz, 2019).[10]
개발 현황
현재 연구되고 있는 양자 컴퓨팅 플랫폼은 크게 초전도체, 이온 트랩, 중성 원자, 다이아몬드 질소 공극 센터, 광자 등이 있다. 이 중 이온 트랩 플랫폼은 이온을 큐비트로 사용하는 광학적 플랫폼으로서, 수많은 기업 및 대학에서 현재 연구들이 진행중이다. 이온 트랩 플랫폼의 경우 게이트 시간이 길다는 단점이 있지만, 큐비트의 결맞음 시간이 다른 종류의 플랫폼에 비하여 훨씬 길다는 장점이 있으며 최근에는 1시간 이상의 단일 큐비트 결맞음 시간이 달성되기도 하였다. 또한 모든 이온 간의 상호 커플링이 쉬워 확장이 용이하다는 장점이 있다. 이러한 장점들로 인하여 IonQ, Honeywell 등의 기업이 현재 최신 이온 트랩 양자 컴퓨팅 하드웨어 개발을 선도하고 있다.
참고 문헌
- ↑ Cirac, J. I., & Zoller, P. (1995), “Quantum computations with cold trapped ions” Physical Review Letters, 74(20) : 4091.
- ↑ Bruzewicz, C. D., Chiaverini, J., McConnell, R., & Sage, J. M. (2019), “Trapped-ion quantum computing: Progress and challenges”, Applied Physics Reviews, 6(2) : 021314.
- ↑ National Academies of Sciences, Engineering, and Medicine. (2019), Quantum Computing: Progress and Prospects. National Academies Press.
- ↑ National Academies of Sciences, Engineering, and Medicine. (2019), Quantum Computing: Progress and Prospects. National Academies Press.
- ↑ Bruzewicz, C. D., Chiaverini, J., McConnell, R., & Sage, J. M. (2019), “Trapped-ion quantum computing: Progress and challenges”, Applied Physics Reviews, 6(2) : 021314.
- ↑ https://en.wikipedia.org/wiki/Hyperfine_structure
- ↑ National Academies of Sciences, Engineering, and Medicine. (2019), Quantum Computing: Progress and Prospects. National Academies Press.
- ↑ Brown, N. C., & Brown, K. R. (2018), “Comparing Zeeman qubits to hyperfine qubits in the context of the surface code: Yb+ 174 and Yb+ 171”, Physical Review A, 97(5) : 052301.
- ↑ Griffiths, D. J., & Schroeter, D. F. (2018), Introduction to Quantum Mechanics. Cambridge University Press.
- ↑ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 Bruzewicz, C. D., Chiaverini, J., McConnell, R., & Sage, J. M. (2019), “Trapped-ion quantum computing: Progress and challenges”, Applied Physics Reviews, 6(2) : 021314.
- ↑ National Academies of Sciences, Engineering, and Medicine. (2019), Quantum Computing: Progress and Prospects. National Academies Press.
- ↑ National Academies of Sciences, Engineering, and Medicine. (2019), Quantum Computing: Progress and Prospects. National Academies Press.
- ↑ National Academies of Sciences, Engineering, and Medicine. (2019), Quantum Computing: Progress and Prospects. National Academies Press.
- ↑ Olmschenk, S., Younge, K. C., Moehring, D. L., Matsukevich, D. N., Maunz, P., & Monroe, C. (2007), “Manipulation and detection of a trapped Yb+ hyperfine qubit” Physical Review A, 76(5) : 052314.
- ↑ Olmschenk, S., Younge, K. C., Moehring, D. L., Matsukevich, D. N., Maunz, P., & Monroe, C. (2007), “Manipulation and detection of a trapped Yb+ hyperfine qubit” Physical Review A, 76(5) : 052314.
- ↑ Debnath, S. (2016), A programmable Five Qubit Quantum Computer using Trapped Atomic Ions (Doctoral dissertation).
- ↑ Olmschenk, S., Younge, K. C., Moehring, D. L., Matsukevich, D. N., Maunz, P., & Monroe, C. (2007), “Manipulation and detection of a trapped Yb+ hyperfine qubit” Physical Review A, 76(5) : 052314.
- ↑ https://en.wikipedia.org/wiki/Trapped_ion_quantum_computer
- ↑ Lee, P. J., Brickman, K. A., Deslauriers, L., Haljan, P. C., Duan, L. M., & Monroe, C. (2005), “Phase control of trapped ion quantum gates”, Journal of Optics B: Quantum and Semiclassical Optics, 7(10) : S371.
- ↑ Lee, P. J., Brickman, K. A., Deslauriers, L., Haljan, P. C., Duan, L. M., & Monroe, C. (2005), “Phase control of trapped ion quantum gates”, Journal of Optics B: Quantum and Semiclassical Optics, 7(10) : S371.
- ↑ Lee, P. J., Brickman, K. A., Deslauriers, L., Haljan, P. C., Duan, L. M., & Monroe, C. (2005), “Phase control of trapped ion quantum gates”, Journal of Optics B: Quantum and Semiclassical Optics, 7(10) : S371.
- ↑ Lee, P. J., Brickman, K. A., Deslauriers, L., Haljan, P. C., Duan, L. M., & Monroe, C. (2005), “Phase control of trapped ion quantum gates”, Journal of Optics B: Quantum and Semiclassical Optics, 7(10) : S371.
- ↑ Olmschenk, S., Younge, K. C., Moehring, D. L., Matsukevich, D. N., Maunz, P., & Monroe, C. (2007), “Manipulation and detection of a trapped Yb+ hyperfine qubit” Physical Review A, 76(5) : 052314.
- ↑ Olmschenk, S., Younge, K. C., Moehring, D. L., Matsukevich, D. N., Maunz, P., & Monroe, C. (2007), “Manipulation and detection of a trapped Yb+ hyperfine qubit” Physical Review A, 76(5) : 052314.
![그림 1 ‑ Hyperfine Qubit의 에너지 레벨 예시(NASEM, 2019).[3]](/images/thumb/3/36/%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image64.png/226px-%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image64.png)
![그림 5 ‑ 단일 큐비트를 표현하는 Bloch sphere(Debnath, 2016).[16]](/images/thumb/b/be/%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image67.png/120px-%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image67.png.jpeg)
![그림 6 ‑ 171Yb+ 이온의 하이퍼파인 큐비트 사이의 Rabi oscillation을 측정한 결과(Olmschenk, 2007).[17]](/images/thumb/f/fb/%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image68.png/143px-%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image68.png.jpeg)
![그림 7 ‑ Cirac-Zoller 게이트의 전이(Lee et al., 2005).[19]](/images/thumb/3/35/%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image69.png/191px-%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image69.png.jpeg)
![그림 8 ‑ Cirac-Zoller 게이트의 모식도(Lee et al., 2005).[20]](/images/thumb/b/b3/%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image70.png/300px-%EC%96%91%EC%9E%90_%EA%B8%B0%EC%88%A0%EB%B0%B1%EC%84%9C_image70.png.jpeg)