광자 기반

양자컴퓨팅의 구현

개요

양자컴퓨팅에서 광자는 큐비트의 주요 구현 방식 중 하나로 연구되고 있으며, 뚜렷한 장점, 즉 특별히 상호작용하는 물질과 접촉하지 않는 이상 환경과 상호작용을 잘 하지 않아 결맞음이 오래 유지된다는 특성이 있다. 또한 이러한 결맞음 특성과 함께 빛의 속도로 빠르게 이동한다는 특성상 멀리 보내기도 수월하다는 장점을 가지고 있다. 이러한 점 때문에 광자는 양자컴퓨팅뿐 아니라 양자통신에서 활발하게 연구되고 있는 주제이기도 하다. 또한 광자 큐비트는 기존의 벌크, 광섬유 기반의 광학 기구를 이용하여 양자 상태를 제어하기에 다른 플랫폼에 비해 시스템 구축이 용이하다는 장점도 가지고 있다.

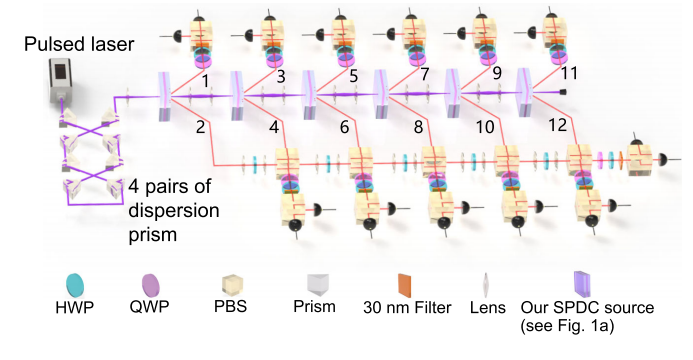
반면에 이러한 특성은 광자 기반 양자컴퓨터의 약점으로 꼽히기도 한다. 광자 간 상호작용은 물론이고 다른 물질을 이용하여 광자의 주파수를 변환하는 비선형 변환의 경우 상호작용 정도가 매우 약하기 때문에 결정론적인 게이트를 만들기 어렵고 확률적인 게이트를 사용할 수밖에 없는 경우가 많다. 또한 이러한 약한 상호작용의 특성과 맞물려 대량의 광자를 얽힘 상태로 만드는 것이 어렵다는 점도 하나의 특징으로 꼽히고 있다. 현재까지 얽힘 상태로 가장 많은 수의 광자를 생성한 것으로 12 광자 얽힘 상태가 알려져 있다 (Zhong, 2018, 그림 2.5‑1 참고).

그림 ‑ 12 큐비트 얽힘 상태 생성의 모식도(Zhong, 2018). 펄스 레이저가 총 6개의 비선형 결정을 통과하며 자발 매개변수적 하향 변환(spontaneous parametric down conversion)에 의해 얽힘 상태인 12개의 광자로 나누어진다.

양자 광학

큐비트==

광자란 일반적인 의미로, 빛으로서 최소 단위 에너지를 갖는 알갱이이다. 광자 기반 양자컴퓨팅에 사용되는 큐비트로는, 광자의 다양한 자유도를 이용한 여러가지 종류가 있다. 우선 선편광 중 한 축의 편광과 그에 수직한 다른 편광을 사용하는 방법이 있다. 선편광된 광자는 편광판이나 편광빔스플리터를 이용해 쉽게 만들 수 있고, 반파장판을 이용해 편광의 각도를 회전시킬 수 있으며, 다시 편광판과 측정기의 조합을 이용해 특정 편광을 측정할 수 있는 등, 큐비트 조작이 용이하기 때문에 광자 기반 양자컴퓨팅 및 기타 광자 관련 실험에 널리 쓰인다. 편광 방향은 일반적으로 광평면에 수평한 수평 방향 편광 $$\left| H \right\rangle$$ 와 그에 수직한 수직방향 편광 $$\left| V \right\rangle$$ 를 많이 사용한다. 이 경우 광자 큐비트 상태 $$\left| \psi \right\rangle$$ 는,

\[\left| \psi \right\rangle= \alpha\left| H \right\rangle + \beta\left| V \right\rangle\]

로 표현할 수 있다 (여기서 $$\alpha,\ \beta$$ 는 $$|\alpha|^{2} + |\beta|^{2} ='"`UNIQ--h-2--QINU`"' 1$$ 인 복소수). 그 밖에 서로 다른 두 주파수를 큐비트의 두 상태로 정하고 이 두 주파수와 반응하는 원자나 결정을 사용하여 큐비트 조작을 하는 방법, 두 개의 공진기나 경로를 만들어놓고 광자가 둘 중 어느 쪽에 있는지를 큐비트의 상태로 이용하는 방법, 궤도 각운동량을 큐비트로써 이용하는 방법 등이 있다. =

결맞음 상태 (Coherent State)==

Coherent state란, 소멸 연산자(annihilation operator) $$\widehat{a}$$ 의 고유상태, 즉

\[\widehat{a}\left| \alpha \right\rangle= \alpha\left| \alpha \right\rangle\]

의 $$\left| \alpha \right\rangle$$ 으로 정의된다. 이 때 $$\alpha = |\alpha|e^{\text{iθ}}$$ 로 나타냈을 때 $$|\alpha|$$는 진폭, $$\theta$$는 위상이라고 부른다. 이는 고전역학에서의 조화 진동자에 있는 입자의 상태를 양자역학적으로 해석할 때 사용하기 위해 고안된 상태로, 위상공간에서는 아래 그림 2.5‑2과 같이 나타낼 수 있다. X와 P는 위상공간의 축을 만드는 쿼드러처(quadrature)이며, 진폭과 위상은 각각 불확정성을 갖고 있다 (Olivares, 2012).

그림 ‑ 위상공간에서의 coherent state $$\left| \alpha \right\rangle$$를 나타낸 그림. X와 P는 쿼드러처(quadrature)이며, $$|\alpha|$$는 진폭, $$\theta$$는 위상이다.

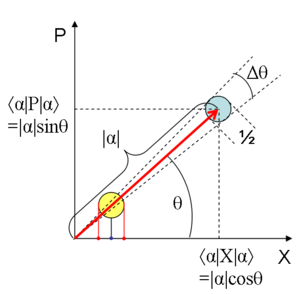
Coherent state의 중요한 특징 중 하나는, 이것이 최소 불확정성 상태, 즉 $$\Delta X ='"`UNIQ--h-3--QINU`"' \Delta P = 1/2$$ 라는 점이다. 여기서 $$\text{ΔX}$$, $$\text{ΔP}$$ 또는 임의의 quadrature로의 불확정성을 줄이는 대신 다른 quadrature의 불확정성을 높인 squeezed state를 만들 수도 있다.

조임 상태 (Squeezed State)

Coherent state에서 하나의 quadrature로 불확정성을 줄인 상태를 squeezed state라고 한다. 이 때 $$\Delta X\Delta P > 1/4$$ 가 되며, 양자광학에서는 일반적으로 두 광자의 squeezing 정도가 이 둘의 양자 얽힘 정도와 관련이 있기 때문에 중요하게 다루어진다 (Marek, 2006).

광학 기구

빔스플리터 (Beam Splitter)==

빔스플리터는 고전광학적으로는 빔을 일정 비율의 출력으로 나눠서 서로 다른 경로로 보내주는 장치이다. 그러나 양자광학적으로는, 단일 광자에 대해 출력을 나누는 것은 불가능하기 때문에 확률적으로 경로가 선택되게 된다. 입력 모드 $${\widehat{a}}_{0}$$, $${\widehat{a}}_{1}$$ 과 출력 모드 $${\widehat{a}}_{2}$$, $${\widehat{a}}_{3}$$ 에 대해 다음과 같이 변환 관계로 나타낼 수 있으며, 이에 따라 확률진폭이 나눠지게 된다.

<math display="block">\begin{pmatrix} {\widehat{a}}_{2} \\ {\widehat{a}}_{3} \\ \end{pmatrix}= \begin{pmatrix} t^{'} & r \\ r^{'} & t \\ \end{pmatrix}\begin{pmatrix} {\widehat{a}}_{0} \\ {\widehat{a}}_{1} \\ \end{pmatrix}

</math>

<math display="block">{\widehat{a}}_{2}

\frac{1}{\sqrt{2}}\left( {\widehat{a}}_{0} + i{\widehat{a}}_{1} \right),\ {\widehat{a}}_{3}

\frac{1}{\sqrt{2}}\left( i{\widehat{a}}_{0} + {\widehat{a}}_{1} \right)

</math>

위상 변이기 (Phase Shifter)

광자의 진행을 늦춤으로서 위상을 변화시키는 장치이다. 빛의 속도를 느리게 하는 물질을 이용하거나, 단순히 액츄에이터 등을 사용해서 경로의 길이를 변화시킴으로써 위상 변화를 만들어줄 수 있다. 양자컴퓨팅에서는, 큐비트를 이루는 두 모드 간의 위상 변화는 곧 큐비트의 국소 위상을 변화시키는 것이기 때문에, 광자 큐비트의 제어에서 필수 부품이라고 할 수 있다.

비선형 물질 (Nonlinear Medium)

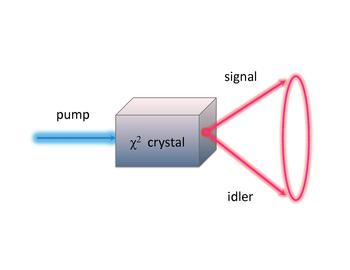
일반적으로 빈 공간상에서 광자끼리는 유의미한 크기의 상호작용을 하지 않는다. 빔스플리터를 이용하여 광자 간 상호작용을 만들어 줄 수 있는데, 비선형 물질을 이용하면 좀 더 다양한 형태의 광자 간 상호작용을 만들어 줄 수 있다. 특히 광자의 파장을 변화시키거나 합치고 나누는 등 광자의 주파수, 즉 에너지를 변환하는 것이 가능하다. 대표적으로 광자 하나를 BBO 결정과 같은 비선형 물질에 통과시켰을 때, 자발 매개변수적 하향변환(spontaneous parametric down conversion)으로 알려진 이차 비선형 효과에 의해 높은 주파수의 단일광자가 낮은 주파수이 이광자로 변환되게 되는데 이때 에너지와 운동량 보존 법칙에 따라 생성되는 이광자간 상관관계가 발생된다 (그림 2.5‑3). 이를 활용하면 편광 또는 주파수 얽힘 광자쌍 생성이 가능하여 양자 광학 실험에서의 중요한 양자얽힘 광원을 제공하고 있고 항상 동시에 쌍으로 생성된다는 특성을 이용하여, 한쪽 경로의 광자를 측정함으로써 다른쪽에 단일광자가 존재함을 알게되는 예고된 단일 광자원(heralded single photon)으로써의 활용 또한 가능하다. 비선형 물질로 가장 많이 이용되는 것은 비선형 결정이지만, 원자 기체나 양자점처럼 광자와 상호작용할 수 있는 다양한 물질들에 대해서도 많은 연구가 이루어지고 있다.

그림 ‑ 자발 매개변수적 하향 변환의 모식도. Pump를 통해 비선형 물질로 입사한 광자는 signal과 idler라고 불리는 두 출력으로 각각 하나의 광자씩 나뉘어 나오게 되며 입력 광자와 출력의 두 광자가 에너지 보존 법칙과 운동량 보존 법칙을 만족하는 조건 하에서 출력 광자가 나오게 된다.

참고 문헌

Olivares, S. (2012), “Quantum optics in the phase space”, The European Physical Journal Special Topics, 203(1) : 3.

Marek, P., Paternostro, M., & Kim, M. S. (2006), “Characterization of the entanglement of two squeezed states”, Physical Review A, 74(3) : 032311.

Zhong, H. S., Li, Y., Li, W., Peng, L. C., Su, Z. E., Hu, Y., ... & Zhang, L. (2018), “12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion”, Physical Review Letters, 121(25) : 250505.

National Academies of Sciences, Engineering, and Medicine. (2019), Quantum Computing: Progress and Prospects, National Academies Press.

Nielsen, M. A., & Chuang, I. (2002), “Quantum computation and quantum information”, American Journal of Physics, 70(5) : 558.