위상 양자 컴퓨팅 (Topological Quantum Computing)

양자컴퓨팅의 구현

양자 정보 오류 (Errors in Quantum Computing)

존 프레스킬 교수는 “우리는 정보가 아닌 오류를 측정한다”고 지적하였다 (John Preskill, 2004). 이는 물리적인 양자 연산에서 오류 처리가 지니는 중요성에 대한 방증이다. 양자 정보 오류를 어떻게 극복할 것인가에 대한 접근법의 차이만으로도 설계하는 양자 컴퓨터의 종류가 상이하게 달라질 수 있다. 현재 주류를 이루고 있는 이온 트랩, 초전도, 그리고 양자점 기반의 큐비트는 $$\left| \left. \ 0 \right\rangle \right.\ $$과 $$\left| \left. \ 1 \right\rangle \right.\ $$ 상태가 하나의 원자 또는 소자 내의 two-level 시스템으로 인코딩 된다는 점에서 국소적(local) 큐비트라고 할 수 있다. 이 시스템들은 구현하는 것이 상대적으로 수월한 반면에, 개별적인 큐비트에 국소적으로 발생하는 오류로 인해 양자 신뢰도 등이 현격히 떨어질 수 있다는 단점을 지닌다. 이와 대조적으로, 물리적인 수준에서 국소적인 섭동(perturbation)에 대하여 불변하는 양자 상태를 구현하여 이를 큐비트로 사용하고자 하는 접근이 존재한다. 그것은 애니온(anyon) 기반의 비국소적 큐비트를 이용하는 위상 양자 연산이다. 애니온이란 위상 물질에서 다체계적 상호작용으로 발현되는 준-입자(quasi-particle)의 한 형태이다.

어떠한 양자 컴퓨터이든 공통적으로 다음과 같이 유니테리 게이트를 통해 양자 연산을 수행하는 패러다임을 따른다: $$\left| \left. \ \psi_{f} \right\rangle = \right.\ U\left| \left. \ \psi_{i} \right\rangle \right.\ $$. 이를 물리적인 관점에서 보았을 때 발생할 수 있는 오류의 종류로는 크게 두 가지가 있다 (Nayak, 2008). 첫 번째는 $$\left| \left. \ \psi_{i} \right\rangle \right.\ $$가 환경과 얽혀서 발생할 수 있는 결깨짐(decoherence)으로 인한 것이고, 두 번째는 unitary 게이트 $$U$$의 불완전성으로 인한 오류이다. 오류 정정 부호가 효력을 발휘하기 위해서는 각각의 오류 사이에 자그마치 $$10^{4} - 10^{6}$$ 개의 완전한 연산이 필요한 것으로 알려져 있다 (Knill, 1998). 국소적 큐비트 기반의 양자 컴퓨터로는 이렇게 강력한 제약 조건을 만족시키기 어려울 것이란 가정 하에, 물리적인 수준에서 두 가지 오류를 원천적으로 극복하고자 하는 접근이 바로 비국소적 큐비트 기반의 위상 양자 컴퓨터이다.

입자 통계과 애니온 (Particle Statistics and Anyons)

3+1 차원의 시공간에 존재하는 모든 입자는 보손(Boson) 또는 페르미온(Fermion)으로 분류될 수 있다. 이는 양자장론으로 증명되는 스핀-통계 정리(spin-statistics theorem)의 결과로 알려져 있다. 입자의 종류는 해당 입자들이 구성하는 파동함수의 대칭성을 결정하여 다체계(many-body)의 특성에 현격한 영향을 미친다. 파동함수의 대칭성이란 구분 불가능(indistinguishable)한 입자를 시공간 상에서 교환(exchange)하였을 때 붙게 되는 위상(phase)을 의미한다. 예를 들어 두 구분 불가능한 입자가 구성하는 파동함수를 $$\psi(r_{1},r_{2})$$, 교환 연산자(exchange operator)를 $$\widehat{P}$$라고 하자. 그러면 $$\widehat{P}\psi\left( r_{1},r_{2} \right) ='"`UNIQ--h-2--QINU`"' \psi\left( r_{2},r_{1} \right) = e^{\text{iθ}}\psi\left( r_{1},r_{2} \right)$$가 성립한다. 보손은 $$\theta ='"`UNIQ--h-3--QINU`"' 0$$, 페르미온은 $$\theta = \pi$$ 에 해당한다.

그러나 2+1 차원의 시공간에서는 입자 교환에 대해 파동함수가 임의의 $$\theta$$를 가질 수 있음이 알려져 있다. 이 입자들을 보손과 페르미온과 구별하여 애니온이라고 부른다. 입자와 대칭성의 관계를 명확히 정의하기 위해서는 군론과 위상학의 형식적 논리가 요구되지만 여기서는 주요 결과만을 간단하게 정리하도록 한다. $$d$$ 차원에서 구분 불가능한 $$N$$ 개 입자들의 짜임새 공간(configuration space)를 $$M_{d}^{N}$$, 이 공간에서 정의된 기본군(fundamental set)을 $$\pi_{1}(M_{d}^{N})$$로 표기하자. 그러면 다음이 성립한다.

<math display="block">\pi_{1}(M_{d}^{N}) \simeq \left\{ \begin{matrix} S_{N}\ \ \ (d \geq 3) \\ B_{N}\ \ \ (d= 2) \\ \end{matrix} \right.\ </math>

$$S_{N}$$은 순환군(permutation group)을, $$B_{N}$$은 꼬임군(braid group)을 가리키고, $$\simeq$$는 동형 사상(isomorphism)을 의미한다. 2 차원 공간에서는 순환군의 대칭성이 깨지면서 꼬임군의 언어를 통해 보손과 페르미온의 일반화된 형태의 입자로 기술되는 애니온의 발현 가능성이 생기는 것이다.

애니온의 시간 변화(time evolution)는 꼬임군이 파동함수에 작용하는 방식에 의해 결정된다 (Nayak, 2008). 이를 수학적인 방식보다는 물리적인 예시를 통해 설명하도록 한다. 애니온은 위상 물질에서 발현되는 준-입자라고 하였는데, 어떤 시스템의 기저 상태를 구성한다고 하자. 기저 상태가 유일하면 가환 애니온(abelian anyon), 축퇴 에너지 준위(degenerate energy level)를 가지는 복수 개가 존재하면 비가환 애니온(non-abelian anyon)이라고 한다. 양자 연산에 사용할 수 있는 애니온은 후자에 해당한다. 비가환 애니온의 교환 연산자는 유니테리 행렬로 표기될 수 있는데, 그림 1.1-1처럼 나타낼 수 있다 (Xinwan, 2006). 가로 축에 놓여 있는 점들은 공간적으로 분리되어 있는 애니온들이고, 세로 축은 시간이다. 시간 변화는 서로 다른 애니온들을 시공간상에서 교환하는 유니테리 연산자에 의해 발생한다. 그림과 꼬임군이라는 이름에서 이유를 알 수 있듯이, 이 유니테리 연산을 ‘braiding’이라고 한다.

그림 2.8‑1 비가환 애니온의 시간 변화 모식도. 서로 다른 애니온들을 시공간상에서 교환하는 유니테리 연산이 시간 변화를 발생시킨다.

비가환 애니온과 위상 양자 연산 (Non-Abelian Anyons and Topological Quantum Computation)

양자 연산은 초기화, 유니테리 변환, 측정이라는 프로토콜을 주로 따르는데(DiVincenzo, 2000), 비가환 애니온 기반의 큐비트 연산 역시 마찬가지다. 애니온의 생성을 통해 양자 상태를 초기화하고, 교환 연산을 통해 유니테리 연산을 하여, 마지막으로 융합 등의 메커니즘으로 측정한다. 여기서 애니온의 생성과 융합에 대한 논의는 생략하도록 한다.

애니온 큐비트 기반의 양자 연산을 위상 양자 연산이라 하는 이유는 비단 이를 기술하는 수학적인 언어가 꼬임군 등의 위상학적 개념에 기반하고 있기 때문만은 아니다. 오히려 애니온이 발현될 수 있는 위상 물질이 다음과 같이 정의되는 물리학적인 의미의 위상적 상(topological phase)의 특성을 가지기 때문이다. 어떤 물리적 시스템이 위상적 상에 있다는 것은 낮은 온도, 낮은 에너지, 그리고 긴 파장대에서 관측 가능한 모든 특성들이 시스템이 속한 시공간 다양체(manifold)의 매끄러운(smooth) 변환에 대하여 불변한다는 것을 의미한다 (Nayak, 2008). 이를 만족하는 물리적 시스템의 예시로는 어떤 것이 있을까?

그림 1.1-2에 나와 있는 모델을 통해 이를 집약적으로 설명할 수 있다 (Lahtinen and Pachos, 2017). 앞서 비가환 애니온은 축퇴 기저 상태를 가진 시스템이라고 했다. 추가적으로, 이 기저 상태들은 에너지 틈(energy gap)을 두고 들뜬 상태(excited states)들과 스펙트럼 상 분리되어 있다. 큐비트와 양자 연산이 정의되는 힐베르트 공간은 바로 이 축퇴 부분 공간(degenerate subspace)이다. 서로 다른 에너지 준위를 가지는 양자 상태를 이용해 $$\left| \left. \ 0 \right\rangle \right.\ $$과 $$\left| \left. \ 1 \right\rangle \right.\ $$을 구분하는 국소적 큐비트와 달리, 애니온 큐비트들은 축퇴 에너지 수준을 가지기 때문에 동적 탈위상(dynamical dephasing)이 발생하지 않는다. 또, 기저 상태와 여기 상태와 에너지 스펙트럼 상 분리되어 있기 때문에 환경과의 상호작용도 이에 비례하여 억제된다는 특성을 가진다.

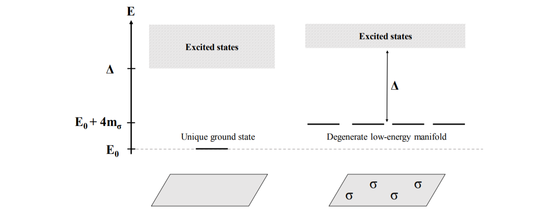
그림 2.8‑2 비가환 애니온들의 에너지 준위 다이어그램. 축퇴(degenerate) 기저 상태들에 의해 생성되는 공간이 위상 양자 연산에 사용되는 힐베르트 공간이다 (Lahtinen and Pachos, 2017).

불완전한 유니테리 연산으로 인한 오류에 대해서도 덜 민감하다. 애니온 큐비트의 시간 변화는 두 애니온을 공간상에서 교환하는 유니테리 연산으로 발생하고, 이를 braiding이라 한다고 하였다. 그런데 braiding은 이산적(discrete)이기 때문에 두 애니온은 완전히 교환되거나, 완전히 교환되지 않는다 (Nayak, 2008). 따라서 불완전한 게이트로 인한 오류가 원천적으로 차단된다. 또한, 개별적인 애니온에 국소적인 섭동이 가해진다고 해도, 완전한 ‘braiding’이 일어나지 않는 이상 전체 양자 상태는 불변하기 때문에 그만큼 환경과의 상호작용에 대해서도 안정적이다. 이러한 이유로 기저 상태의 비가환 애니온들에 의해 정의되는 힐베르트 공간을 보호된 부분 공간 (protected subspace)이라고 한다. 양자 위상 연산은 바로 이러한 비국소적 안정성을 성취할 수 있다는 가능성에 힘입어 각광을 받아왔다. 그런데 왜 아직 이를 구현한 하드웨어에 대한 소식이 국소적 양자 컴퓨터에 비해 저조한 것일까? 그것은 애니온을 만드는 것이 매우 어렵기 때문이다.

참고 문헌

Preskill, J. (2004). “Lecture notes for physics 219: Quantum computation” available at http://www.theory.caltech.edu/~preskill/ph219/ph219_2004.html

Nayak, C., Simon, H. S., Stern, A., Freedman, M., & Das Sarma, S. (2008), “Non-Abelian anyons and toplogical quantum computation”, Reviews of Modern Physics, 80(3) : 1083.

Knill, E., Laflamme, R., & Zurek, W. H. (1998), “Resilient quantum computation: error models and thresholds”, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 454(1969) : 365.

DiVincenzo, D. P. (2000), “The physical implementation of quantum computation”, Fortschritte Der Physik, 48(9-11) : 771.