양자 암호 통신

한국양자정보학회 위키
둘러보기로 이동 검색으로 이동
인쇄용 판은 더 이상 지원되지 않으며 렌더링 오류가 있을 수 있습니다. 브라우저 북마크를 업데이트해 주시고 기본 브라우저 인쇄 기능을 대신 사용해 주십시오.



양자 키 분배

통신자가 암호화된 방식으로 안전하게 통신하기 위해서는 외부에 공개되지 않은 비밀키(secret key)를 분배하는 것이 필수적이다. 양자 키 분배란 양자 물리계의 고유한 특성을 활용하여 통신자 간 비밀키를 공유하는 기술을 말한다. 현재 암호 체계에서 가장 잘 알려진 RSA(Rivest-Shamir-Adleman) 암호 체계의 안전성은 큰 수의 소인수분해의 계산 복잡도에 의존한다. 따라서 RSA 방식은 소인수분해 문제를 풀기에 충분한 성능의 컴퓨터가 고안되면 암호 체계의 허점이 생긴다는 단점이 있다. 양자 키 분배에서는 키 분배 안전성이 양자 물리학 법칙에 의존하므로, 안전성이 수학적 복잡성이 아니라 물리 법칙에 기반한다는 장점이 있다. 양자 키 분배 과정에서 도청 행위가 있을 경우, 통신자는 측정 오류를 비교함으로써 도청자의 존재를 확인할 수 있다.

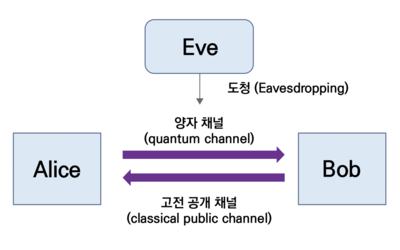
그림 1. 양자 키 분배 프로토콜 개요도. 통신자(Alice/Bob)는 도청자(Eve)의 도청 여부를 공개 채널을 통한 전송 오류율 계산을 통하여 확인할 수 있다.

두 통신자 Alice와 Bob이 서로 통신한다고 가정할 때, 양자 키 분배 프로토콜은 다음의 과정을 통해 이루어진다. 우선 양자 채널을 통하여 양자 상태가 분배된다. 양자 채널로는 광섬유가 주로 활용되며, 시야가 확보된 자유 공간(free space)에서도 양자 키 분배를 구현할 수도 있다. 광섬유를 활용한 509km 거리간 양자 키 분배와 자유 공간에서 위성을 사용한 대륙간 양자 키 분배가 실험을 통하여 구현된 바 있다.[1][2] Alice는 양자 상태에 난수 발생기로부터 무작위하게 생성된 정보를 단일광자의 편광이나 시간 빈에 부호화(encoding)하여 전송한다. 논의를 단순화하기 위하여, 0과 1이 무작위로 생성되는 2차원 난수 발생기를 활용한다고 가정한다. 도청을 방지하기 위해서는 순수 난수 발생기(true random number generator)를 활용해야 한다. 이 때, 도청자 Eve가 전송된 양자 상태를 측정하면, 양자 역학적 과정에 의해 단일 광자의 양자 상태가 교란되고 통신자는 교란된 전송 오류를 확인하여 도청의 존재를 확인할 수 있다. 따라서 도청의 존재를 확인하기 위해서는 전송 오류를 확인하는 과정이 중요하다. Alice와 Bob이 서로 교환한 신호를 비교하고, 전송 오류를 확인하기 위한 목적으로 주로 고전적인 공개 채널(public channel)이 활용된다. 이 때 채널은 반드시 공개 채널일 필요가 없으나, 공개되지 않은 비밀 채널(private channel)일 경우 굳이 암호 키 분배를 할 필요가 없으므로 일반적으로 공개 채널이 가정된다.[3] 공개 채널을 통해 도청의 존재를 확인될 경우 생성된 키는 버려지고 새로운 키 분배 프로토콜을 수행한다.

BB84 (Bennett-Brassard 1984) 프로토콜

1984년, Bennett과 Brassard가 제안한 BB84 양자 키 분배 프로토콜은[4] 35년이 지난 현재까지(2020년 기준) 가장 빈번하게 활용되는 양자 키 분배 프로토콜 중 하나이다. BB84 프로토콜은 현재까지 다양한 실험에서 구현된 바 있으며[5][6][7], BB84에 기반한 양자 키 분배 장치는 실험을 넘어 상업적 용도로 활용되고 있기도 하다. 아래 내용을 통하여, BB84 프로토콜에 대하여 설명한다.

BB84 프로토콜은 두 통신자가 큐비트 양자 상태를 정보의 전송 수단으로 활용하는 방식의 프로토콜이다. 두 통신자를 Alice와 Bob, 활용되는 큐비트를 디랙 표기법에 따라 $$\alpha|0\rangle + \beta|1\rangle $$로 표기하도록 하자. Alice는 무작위로 0과 1의 정보를 큐비트에 부호화(encoding)한다. 이 때 무작위한 0과 1은 암호키 요소(key element)에 해당한다. 부호화 규칙은 다음과 같다. 0의 경우, 상태 $$|0\rangle$$ 또는 상태 $$\left| + \right\rangle= (|0\rangle + |1\rangle)/\sqrt{2} $$로 무작위로 부호화 된다. 상태 $$|0\rangle$$과 상태 $$\left| + \right\rangle$$이 부호화 될 확률은 동일해야 한다. 1의 경우, 역시 무작위로 상태 $$|1\rangle$$ 또는 상태 $$\left| - \right\rangle =(|0\rangle - |1\rangle)/\sqrt{2}$$로 부호화 된다. Alice는 양자 채널을 활용하여 부호화 된 암호키 요소를 Bob에게 전달한다.

Bob은 Alice로부터 전달받은 양자 상태에 부호화된 정보를 복호화(decoding) 하는 측정을 수행한다. 만약 Bob이 선택한 측정의 측정 기저가 상태 $$|0\rangle$$과 $$|1\rangle$$이라면, Alice가 보낸 $$|0\rangle$$과 $$|1\rangle$$ 상태를 구분할 수 있다. 하지만 Alice가 보낸 상태가 $$\left| + \right\rangle$$ 또는 $$\left| - \right\rangle$$라면, 두 경우 모두에 대하여 양자역학에 따라 각각 1/2 확률로 0 또는 1의 측정 결과를 얻을 것이다. 결과적으로 상태 $$\left| + \right\rangle$$, $$\left| - \right\rangle$$는 구분할 수 없게 된다. 복호화하기 위해 Bob의 측정 기저는 매우 중요한 역할을 한다. BB84 프로토콜에서는 Bob이 상태 $$|0\rangle$$/$$|1\rangle$$을 구분하기 위한 기저와, 상태 $$| + \rangle$$/$$| - \rangle$$을 구분하기 위한 기저를 1/2 확률로 선택한다. 결과적으로 Bob은 측정 결과 절반의 확률로 정확한 값을 얻는다. 상기의 부호화된 큐비트를 전달하고 Bob이 측정하는 시행을 여러 번 반복한다.

표 1. BB84 프로토콜에서 5개 암호키 요소에 대한 Alice의 부호화와 Bob의 복호화 과정 예시.
Alice 암호키 요소 1 0 1 1 0
부호화 상태 $$| - \rangle$$ $$| 0 \rangle$$ $$| 1 \rangle$$ $$| 1 \rangle$$ $$| + \rangle$$
Bob 측정 기저 $$| + \rangle$$/$$| - \rangle$$ $$|0\rangle$$/$$|1\rangle$$ $$| + \rangle$$/$$| - \rangle$$ $$|0\rangle$$/$$|1\rangle$$ $$|0\rangle$$/$$|1\rangle$$
측정 결과 상태 $$| - \rangle$$ $$| 0 \rangle$$ $$| 0 \rangle$$ $$| 1 \rangle$$ $$| 0 \rangle$$
암호키 요소 1 0 0 1 0

충분한 시행이 이루어진 후, Alice는 Bob에게 자신이 부호화할 때 사용한 측정 기저의 종류를 공유한다. Bob은 이를 통해 어떤 시행에 대하여 자신이 잘못된 측정 기저를 사용했는지 알 수 있다. 결과적으로 잘못된 측정을 사용한 경우에 대한 결과는 버려진다. 이 과정을 시프팅(sifting) 과정이라 하며, 이 과정을 통해 걸러진 비밀키를 시프트 키(sifted key)라 한다. 시프팅 과정 결과 통신자 Alice와 Bob은 서로 암호 키를 공유할 수 있다. 상기 표에서 나타난 예시에서 Alice와 Bob은 시프팅 과정을 통하여 세 번째, 다섯 번째 측정 결과를 거르고, '101'의 시프트 키를 공유한다.

BB84 프로토콜에서 Alice와 Bob의 전송 신호를 도청자 Eve가 도청할 경우, Alice와 Bob은 도청자의 존재를 확인할 수 있다. 만약 Eve가 양자 상태 전달체인 특정 광자 신호를 가로채서 측정한 후 Bob에게 전달하는 경우를 가정하자. 이 때 Eve의 측정은 불가피하게 Alice와 Bob 사이 공유된 결과에 오류를 낳는다. 만약 Eve가 Alice가 선택한 측정 기저와 동일한 기저를 선택하여 측정한다면, Eve가 가로챈 양자 상태에 측정한 결과는 Alice가 전송한 양자 상태와 동일하므로, Bob이 Eve의 존재를 알 수 없다. 반면, Eve와 Alice의 측정 기저가 다를 경우, Bob의 측정 결과에 오류를 가져온다. 예를 들어 Alice가 전송한 $$| + \rangle$$ 상태를 Eve가 가로채 $$|0\rangle$$/$$\left| 1 \right\rangle$$의 기저로 측정한 상황을 가정해 보자. 이 때, Eve의 측정 결과는 1/2 확률로 $$|0\rangle$$ 또는 $$\left| 1 \right\rangle$$이다. Eve가 측정한 후 전송한 신호에 대하여 Bob은 어떤 기저로 측정하던 1/2 확률로 $$|0\rangle$$ 또는 $$\left| 1 \right\rangle$$ 상태를 얻는다. 결과적으로 Eve가 Ailce와 다른 기저를 선택할 확률 1/2과 그 때 Bob이 잘못된 결과를 얻을 확률 1/2를 곱하여 1/4의 확률로 오류가 발생한다.

최종적으로 Eve의 측정이 만든 오류는 Alice와 Bob이 전송 오류를 측정하여 확인된다. Alice와 Bob은 전체 키 중에서 일부의 키를 추출하여 서로 공유한 시프트 키가 정확히 맞는지 확인한다. 도청자 이외의 오류 발생원에 대한 효과를 이론적으로 배제한다면, 오류를 통하여 도청이 존재함을 알 수 있다. 충분히 많은 시행의 결과로 추출한 크기가 큰 비트열에서 오류가 없다면, 이는 통계적으로 높은 확률로 도청이 존재하지 않음을 시사한다.

양자 난수 발생기(Quantum Random Number Generator)

난수성은 양자 키 분배, 비국소 상관관계 측정 등 양자 통신을 포함한 양자정보 이론의 다양한 분야에서 활용되는 자원이다. 결정론적인 알고리듬에 기반하여 난수를 생성하는 난수 발생기를 유사 난수 발생기는 PRNG(pseudo random number generator)라 한다. 이에 반하여 무작위한 물리적 과정에 기반하여 난수를 생성하는 순수 난수 발생기를 TRNG(true random number generator)라 한다. 양자 난수 발생기(quantum random number generator; QRNG)는 양자역학의 비결정론적 현상에 기반하여 난수를 생성한다.

그림 2. 빔분할기(beam splitter)를 통과하는 단일 광자 경로 개요도. 경로 a, b를 통과한 광자는 각각 검출기 D1, D2에서 검출된다.

양자 난수 발생기는 다양한 양자광학적 현상에 기반하여 고안되었다. 예컨대, 분기 경로 발생기(branching path generators), 도착 시간 발생기(time of arrival generators), 광자 수 발생기(photon counting generators), 감쇠된 펄스 발생기(attenuated pulse generators) 등이 고안된 바 있다.[8] 본 항목을 통하여 가장 빈번하게 활용되고 있는 난수 발생기 중 하나인, 분기 경로 발생기에 대하여 간단히 설명한다. 위 그림과 같이 광원에서 생성된 단일 광자가 빔분할기(beam splitter)에 입사되어 반사 경로 $$a$$로 진행하거나 투과 경로 $$b$$로 진행하게 되는 상황을 가정하자. 경로 $$x \in \{ a,b\}$$에 광자가 $$n \in \{ 0,1\}$$개 존재하는 상태를 $$\left| n \right\rangle_{a}$$라 표기한다. 이 때 빔분할기를 활용하면 다음과 같은 중첩 상태를 준비할 수 있다.

\[{\frac{\left| 1 \right\rangle_{a}\left| 0 \right\rangle_{b} + \left| 0 \right\rangle_{a}\left| 1 \right\rangle_{b}}{\sqrt{2}}}\]

따라서 반사 경로 $$a$$를 따라 D1검출기에서 광자가 1개 포착될 확률과 투과 경로 $$b$$를 따라 D2검출기에서 광자가 1개 검출될 확률은 모두 $$1/2$$로 동일하다. 이제 D1검출기에서 광자가 포착되는 경우 0비트, D2검출기에서 광자가 포착되는 경우 1비트를 입력한다고 하면 0과 1의 완전한 무작위의 난수를 생성할 수 있다.

양자전송(Quantum Teleportation)

양자전송(quantum teleportation)이란 한쪽 양자 상태의 정보를 떨어져 있는 다른 장소로 옮기는 기술을 말한다. 양자 전송을 통하여 송수신자는 양자 통신 채널 없이도 정보를 전달할 수 있다. 양자전송은 양자 중계기(quantum repeater)와 같은 통신 수단의 기초가 되는 중요한 기술 중 하나이다. 다음의 예시[9]를 통하여 양자전송에 대하여 간단히 설명한다.

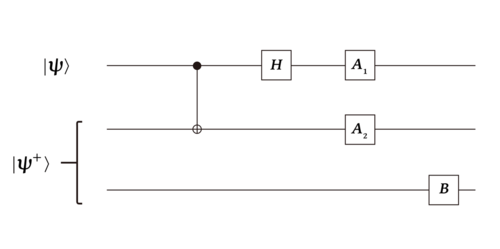
그림 3. 양자전송 개요도. 위의 두개 선은 Alice의 상태, 가장 아래 선은 Bob의 상태를 나타낸다. Alice와 Bob 사이의 얽힘 상태 $$\left| \psi^{+} \right\rangle$$를 활용하여, 임의의 큐비트 상태 $$\left| \psi \right\rangle$$에 대한 정보가 Bob에게 전송된다. --> 그림 수정필요 : Alice의 상태 확인결과에 따른 피드 포워드 작용이 추가되어야 함.

통신자 Alice와 Bob이 초기에 서로 간 벨 상태 $$\left| \psi^{+} \right\rangle= (|00\rangle + |11\rangle)/\sqrt{2}$$를 생성하고, 멀어진 상황을 가정하자. 양자전송은 초기에 공유한 양자 상태와 추가적인 고전 통신을 사용하여 Alice가 자신도 정확히 알지 못하는 임의의 큐비트 상태 $$\left| \psi \right\rangle =\alpha\left| 0 \right\rangle + \beta\left| 1 \right\rangle$$ 를 Bob에게 전송하는 것을 가능케 한다. 위 그림의 양자 회로를 통하여 양자전송의 과정을 보다 구체적으로 설명할 수 있다.

Alice가 초기에 가진 상태는 $$\left| \psi_0 \right\rangle = \left| \psi \right\rangle \left| \psi^{+} \right\rangle$$이다. 이제 Alice가 자신이 가진 큐비트들을 CNOT 게이트에 통과시킨 후 첫번째 큐비트 $$\left| \psi \right\rangle$$만 하다마드 게이트(hadamard gate)에 통과시킨다. 최종적인 상태는 다음과 같다.

\[\left| \psi' \right\rangle= \frac{1}{2}\lbrack |00\rangle(\alpha\left| 0 \right\rangle + \beta\left| 1 \right\rangle) + \left| 01 \right\rangle\left( \alpha\left| 1 \right\rangle + \beta\left| 0 \right\rangle \right) + \left| 10 \right\rangle\left( \alpha\left| 0 \right\rangle - \beta\left| 1 \right\rangle \right) + |11\rangle(\alpha\left| 1 \right\rangle - \beta\left| 0 \right\rangle) \rbrack\]

Alice는 자신의 가진 큐비트들을 A1, A2 측정을 통해 측정한다. 측정 결과는 00, 10, 01, 11의 총 네 가지 경우의 수가 나올 수 있으며, 그 때마다 Bob이 얻게 되는 상태도 결정된다. 최종적으로 Bob은 Alice에게 고전 채널을 통해 전달받은 측정 정보에 따라 자신이 가진 벨 상태의 큐비트에 적절히 상태 보정 작업을 수행하여 Alice가 보내고자 한 $$\left| \psi \right\rangle$$ 상태를 얻을 수 있다. 그림의 개요도 상 B 게이트는 Bob이 A1이나 A2 측정 결과에 따라 수행해야 할 양자 게이트를 나타낸다. Bob이 Alice로부터 00의 정보를 얻게 된다면, Bob의 상태는 이미 $$\left| \psi \right\rangle$$와 동일하므로 아무런 작업을 수행하지 않아도 된다. Bob이 01, 10, 11의 측정 결과를 전송받은 경우, 각각 X 게이트, Z 게이트, ZX 게이트에 해당하는 양자 연산을 수행하여 받고자 하는 $$\left| \psi \right\rangle$$ 상태를 구할 수 있다.


양자전송은 마치 상대성 이론을 위배하는 것처럼 보일 수 있다. 상대론에 의하면 정보는 빛보다 빠르게 전달될 수 없으나, 양자전송에서 큐비트는 Alice에게서 Bob으로 순간적으로 전송되는 것처럼 보이기 때문이다. 그러나 상기한 바와 같이 Alice와 Bob은 반드시 고전 채널을 통해 정보를 전달을 해야 하며, 이로 인해 빛보다 빠르게 양자전송을 수행할 수 없다. 양자전송은 양자 채널을 통한 단일 큐비트 통신을, 얽힘 상태의 공유와 고전 통신의 이용의 조합으로 대체할 수 있음을 보여줄 뿐이다. 또 한 가지 유의해야 할 점은 양자전송이 양자정보 이론의 “복제-불가능 정리”를 위배하지 않는다는 사실이다. 위의 양자전송 시나리오에 따르면 전송의 결과로 Bob에게만 $$\left| \psi \right\rangle$$ 큐비트가 존재하고 Alice가 갖고 있던 큐비트는 측정에 의해 $$\left| 0 \right\rangle$$또는 $$\left| 1 \right\rangle$$상태로 투영되기 때문이다. 양자전송에 관한 연구는 해당 개념이 1993년 처음 제안된 이후로[10], 주로 광자의 큐비트 상태 전송을 통해 실험되어왔다. 2019년에는 광자의 3차원 상태를 양자전송한 실험 결과가 최초로 보고되었다[11].

참고 문헌

  1. ↑ J. P. Chen et al., Sending-or-Not-Sending with Independent Lasers: Secure Twin-Field Quantum Key Distribution over 509 km, Physical Review Letters 124(7), (2020). doi:: 10.1103/PhysRevLett.124.070501.
  2. ↑ S. K. Liao et al., Satellite-relayed intercontinental quantum network, Physical Review Letters 120(3), (2018). doi:: 10.1103/PhysRevLett.120.030501.
  3. ↑ Van Assche. G, Quanrum Cryptography and Secret-key Distillation (Cambridge University Press 2006).
  4. ↑ C. H. Brassard, C. H. Bennett, Quantum Cryptography: Public key distribution and coin tossing, arXiv:2003.06557.
  5. ↑ P. A. Hiskett et al., Long-distance quantum key distribution in optical fibre, New Journal of Physics 8(9), (2006). doi:10.1088/1367-2630/8/9/193.
  6. ↑ Schmitt-Manderbach et al., Experimental demonstration of free-space decoy-state quantum key distribution over 144 km, Physical Review Letters 98(1), (2007). doi : 10.1103/PhysRevLett.98.010504 .
  7. ↑ A. R. Dixon et al., Gigahertz decoy quantum key distribution with 1 Mbit/s secure key rate, arXiv:0810.1069.
  8. ↑ M. Herrero-Collantes, J. C. Garcia-Escartin, Quantum random number generators, Reviews of Modern Physics 89(1), (2017), doi : 10.1103/RevModPhys.89.015004.
  9. ↑ M. A. Nielsen & I. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, 2002).
  10. ↑ C. H. Bennett et al., Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels, Physical Review Letters 70(13), (1993), doi : 10.1103/PhysRevLett.70.1895.
  11. ↑ Y. H. Luo et al., Quantum teleportation in high dimensions, arXiv:1906.09697.
원본 주소 "https://wiki.qisk.or.kr/index.php?title=양자_암호_통신&oldid=3594"