확장성 (Scalability), 양자 볼륨 (Quantum Volume)
<양자 기술백서 |
┗<양자컴퓨팅의 구현|
┗|클라우드 양자컴퓨팅>
확장성 (Scalability)

확장성이란 연산 가능한 큐비트 수의 증가를 의미한다. 아직 양자 우위를 확실하게 실현하지 못하는 이유 중에 하나가 연산 가능한 큐비트 수가 현재는 적기 때문으로 확장성은 현재 양자컴퓨터 개발에서 플랫폼을 가리지 않고 공통적인 목표로 여겨진다. 구글의 양자컴퓨터 시카모어(Sycamore)는 2019년 기준 53 큐비트를 구현하였고, IBM의 Hummingbird는 2021년 기준 65 큐비트 구현하였다. 이 두 프로세서는 초전도체 플랫폼에서 트랜스몬 큐비트를 구현하였으며, 현재까지 가장 확장성이 뛰어난 플랫폼으로 알려져있다. 하지만, 초전도체 플랫폼의 경우 게이트의 양자 신뢰도가 상대적으로 낮다는 단점이 있다. 이와 반대로, 이온 트랩 플랫폼은 신뢰도는 높지만 트랩 구조 상 100개 이상의 많은 이온을 포획하고 양자 제어하는 것이 어려워 확장성에 대한 한계가 존재한다. Honeywell은 게이트의 양자 신뢰도가 높은 이온 트랩기반에서 뛰어난 확장성의 양자컴퓨터를 개발하고 있다. 현재 Honeywell에서 발표한 Model H1 칩에서 10 큐비트를 포획했지만, 구조적으로는 40개까지 가능하며, Model H1의 목표는 40 큐비트까지 높이는 것이 목표인 것으로 알려져 있다.
그리고 최근에는, 아래에서 기술될 “양자 볼륨(quantum volume)”이라는, 큐비트의 개수와 양자 신뢰도를 종합해서 평가하는 개념으로 확장성을 표현하는 추세인데, Honeywell에서는 2021년 3월, 512의 양자 볼륨을 달성했다고 발표했다.[2] 이 시스템에서 단일 큐비트 게이트 신뢰도는 99.991(8)%, 2-큐비트 게이트 신뢰도는 99.76(3)%, 측정 신뢰도 99.75(3)%로 알려졌다. 2020년 8월 IBM에서는 27-큐비트 양자컴퓨팅 시스템인 몬트리올(Montreal)을 공개했고, 그 후 2020년 12월, 같은 시스템이 테스트를 통해 양자 볼륨 128로 발표되었다.[3] (2021년 4월 현재 양자 볼륨 64에 대해서까지만 논문으로 발표되어있다.)[4]

양자 볼륨 (Quantum Volume)
양자 볼륨(quantum volume)은 2018년 IBM의 연구단에서 발표한 논문에서 제시된 양자컴퓨터의 성능을 나타내는 지표이다.[6] 양자컴퓨터가 고전 컴퓨터보다 강점을 갖는 이유는 큐비트들의 중첩과 얽힘이 가능하기 때문이다. 그리고 현재의 양자 컴퓨터는 고전 컴퓨터에 비해 에러에 매우 취약하다. 따라서 양자 컴퓨터의 성능을 나타내기 위해 물리적 큐비트의 수 N, 큐비트 간의 연결성, 에러가 일어나기 전에 진행할 수 있는 게이트의 수 총 3가지 요인이 반영되어야 한다. 이 3가지 요인은 양자 컴퓨터가 만들 수 있는 최대의 양자 회로도 크기를 결정한다. 물리적 큐비트 수 N과 큐비트 간 연결성은 양자회로도에서 세로 길이를, 에러가 일어나기 전에 진행할 수 있는 게이트의 수는 가로 길이를 나타낸다. 단일 큐비트 게이트만 사용하면 가로길이가 길어질 수 있지만 유의미한 양자컴퓨터의 성능을 나타내지 않는다. 따라서 가로 길이를 나타냄에 있어 단순히 진행할 수 있는 게이트의 수를 사용하는 것은 적절치 않다. 알고리듬을 사용할 수 있는 유의미한 양자회로도의 가로길이를 나타내기 위해 회로 깊이 d를 정의한다. 회로 깊이는 에러가 일어나기 전에 얼마나 많은 임의의 2 큐비트 병렬연산을 할 수 있는 지를 의미한다.
가장 간단한 양자 컴퓨터의 성능척도는 양자회로도의 넓이를 나타내는 물리적 큐비트의 수 N과 회로깊이 d의 곱이다. 하지만 이 두 수의 곱이 양자컴퓨터의 성능 지표로서 적절치 않은 이유는 알고리듬을 돌리기 어려운 상황에서도 큰 값이 계산되기 때문이다. 큐비트 간의 연결이 거의 없이 단순히 물리적 큐비트가 많은 경우 d=1이지만 N이 매우 커서 Nd의 값이 커질 수 있다. 반대로 큐비트가 2개 밖에 없지만 2 큐비트 게이트의 충실도가 굉장히 높은 경우 N=2지만 d가 매우 커져 Nd의 값이 커질 수 있다. 이에 IBM의 연구단은 2018년도에 이상적인 양자볼륨으로 N과 d중 작은 값의 제곱으로 정의했다.
\[{\widetilde{V}}_{Q}= {\min\left\lbrack N,d(N) \right\rbrack}^{2}\]
여기서 이상적임의 의미는 큐비트를 연산할 때 신호혼선이 없어 큐비트의 수가 늘어남에 따라 2 큐비트 연산의 에러율이 증가하지 않는 것을 의미한다. 회로 깊이는 큐비트의 플랫폼에 따라 다른 특성을 보인다. 먼저 임의의 2 큐비트 연산의 에러율을 $${\epsilon}$$이라 하면 모든 큐비트가 연결된 경우 임의의 2 큐비트 연산의 실질 에러율은 임의의 2 큐비트 연산의 에러율과 동일하다
\[\epsilon_{eff}=\epsilon\]
시카모어 칩과 같이 2차원 평면에서 가장 가까운 이웃 큐비트만 연결되어 있는 경우 임의의 2 큐비트 연산의 실질 에러율을 물리적 큐비트 수 N에 영향을 받게 된다.
\[\epsilon_{eff}=\sqrt{N}\epsilon\]
1의 회로깊이 만큼의 알고리듬 진행되었을 때 에러가 발생할 확률은 물리적 큐비트의 수(N)와 2 큐비트 연산의 실질 에러율($${\epsilon_{eff}}$$)의 곱에 비례하게 된다. 따라서 양자컴퓨터의 회로 깊이(d)는 물리적 큐비트 수와 2 큐비트 연산의 에러율을 통해 예측할 수 있다.
\[d \approx \frac{1}{N\varepsilon_{\text{eff}}}\]
큐비트 간의 혼선이 있을 경우에는 큐비트를 많이 운용할수록 2 큐비트 연산의 에러율이 증가하기 때문에 적절한 큐비트 수만을 운용하는 것이 더 큰 양자 볼륨을 보이기도 한다. 이를 고려한 양자 볼륨은 다음과 같다.
\[V_{Q}= \max_{n < N}\left\{ {\min\left\lbrack n,\frac{1}{n\varepsilon_{\text{eff}}(n)} \right\rbrack}^{2} \right\}\]
현재까지는 양자 볼륨을 이용해서 양자컴퓨터의 성능을 측정하고 있지만, 양자컴퓨터의 종합적인 성능을 판단하기엔 너무 적은 변수로 판단한다는 한계를 가졌다는 의견이 있다. 또한 양자컴퓨터의 플랫폼마다 특징이 다양하고 성능이 다 다른데 이를 고려하지 않았다는 지적도 있다. 하지만 현재까지는 단순히 큐비트의 개수를 제시하는 것보다는 더 많은 정보를 제공하기 때문에 공통적으로 사용되는 추세이다.
이온 트랩 기반 양자컴퓨터의 경우 모든 큐비트 간 얽힘을 만들 수 있어, 비슷한 큐비트 개수를 가진 다른 플랫폼에 비해 양자 볼륨이 높게 측정된다. 2021년 3월에 Honeywell에서 10-큐비트 양자컴퓨터인 H1에서 양자 볼륨 512가 측정된 데 이어,[7] 그리고 아직 실험적으로 테스트 되기 전이긴 하지만, 12월에 IonQ에서 발표한 32-큐비트 양자컴퓨터는 4,000,000 양자 볼륨이 측정될 것으로 기대된다는 발표가 있었다.[8] 마지막 설치단계만 남아서, 게이트의 신뢰도는 99.9%를 유지하고 이온의 수만 증가하는 것이라 계산된 4백만이란 값에 확신을 가진다고 하였으며, 또한 값이 너무 커지는 것을 고려해서 IonQ는 다음과 같이 새로운 단위인 AQ (algorithmic qubits)를 제안하기도 하였다.
\[AQ= \log_{2}{(QV)}\]
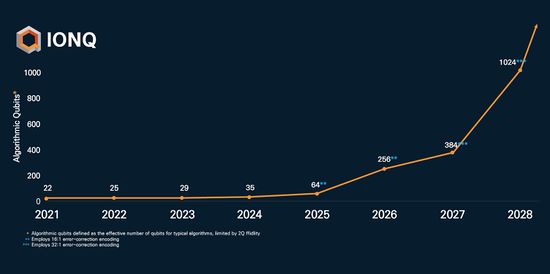
여기서 QV는 양자 볼륨으로, 기하급수적으로 커지는 양자 볼륨을 로그를 취한 값이다. IonQ의 32-큐비트 양자컴퓨터는 22 AQ이다. IonQ는 로드맵을 소개하면서 2023년엔 머신러닝 연산이 가능할 것이고, 80 ~ 150 AQ부터 양자 우월성을 보여줄 것이라 발표했다.[6][9][10][11][12]
참고 문헌
- ↑ https://newsroom.ibm.com/media-quantum-innovation?o=100#gallery_gallery_0:21596
- ↑ https://www.honeywell.com/us/en/news/2021/03/honeywell-sets-new-record-for-quantum-computing-performance
- ↑ https://twitter.com/jaygambetta/status/1334526177642491904
- ↑ Jurcevic, P. et al. Demonstration of quantum volume 64 on a superconducting quantum computing system. Quantum Science and Technology 6, 025020, (2021). doi: https://doi.org/10.1088/2058-9565/abe519.
- ↑ https://www.honeywell.com/us/en/news/2020/10/get-to-know-honeywell-s-latest-quantum-computer-system-model-h1
- ↑ 6.0 6.1 Moll, N. et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Science and Technology 3, 030503, (2018). doi: https://doi.org/10.1088/2058-9565/aab822.
- ↑ https://www.honeywell.com/us/en/news/2021/03/honeywell-sets-new-record-for-quantum-computing-performance
- ↑ https://ionq.com/posts/december-09-2020-scaling-quantum-computer-roadmap
- ↑ Wang, Y., Li, Y., Yin, Z.-q., and Zeng, B. 16-qubit IBM universal quantum computer can be fully entangled. npj Quantum Information 4, 46, (2018). doi: https://doi.org/10.1038/s41534-018-0095-x.
- ↑ J, A. et al. Quantum Algorithm Implementations for Beginners. arxiv:1804.03719.
- ↑ Linke, N. M. et al. Experimental comparison of two quantum computing architectures. Proceedings of the National Academy of Sciences 114, 3305, (2017). doi: https://doi.org/10.1073/pnas.1618020114.
- ↑ Goodfellow, I. J. et al. in Proceedings of the 27th International Conference on Neural Information Processing Systems - Volume 2 2672–2680 (MIT Press, Montreal, Canada, 2014).
- ↑ https://ionq.com/posts/december-09-2020-scaling-quantum-computer-roadmap