양자역학 개요

한국양자정보학회 위키
Byeol Kang (토론 | 기여)님의 2021년 9월 15일 (수) 10:16 판
둘러보기로 이동 검색으로 이동

<양자 기술백서 |

       ┗|양자컴퓨팅의 구현>

              ┗|양자정보 개요>


큐비트 (Qubit)

큐비트는 양자 비트(quantum bit)의 약어로서, 양자정보 양(quantity)의 기본 단위이다. 큐비트와 고전 비트의 중요한 차이 중 하나는 큐비트가 2차원의 양자 상태로 표현된다는 점에 있다. 양자 상태를 정보량의 단위로 사용할 경우 양자역학의 고유한 현상들이 정보량을 정의하는 데에 중요해지므로, 큐비트를 단위로 하는 정보는 기존의 고전 정보와 완전히 다른 성격을 갖게 된다. 고전 비트가 0과 1 사이의 선택인데 비해, 큐비트는 일반적으로 상태 $$\left.|0 \right\rangle$$과 상태 $$\left.|1 \right\rangle$$의 다음과 같은 중첩 상태로 표현된다.

\[\alpha|0\rangle + \beta|1\rangle\]

이때, $$\alpha$$, $$\beta$$ 값은 복소 값으로 정의되며, $$\alpha$$, $$\beta$$가 0 또는 1 값을 가질 때 주어지는 상태 $$\left. |0 \right\rangle$$과 $$\left. |1 \right\rangle$$은 계산 기저상태(computational basis states)라 부른다. 고전 비트값을 측정하는 상황을 가정하면 그 값이 0일 경우 0으로, 1일 경우 1로 결정론적으로 측정될 것이다. 큐비트를 측정하는 상황은 이보다 조금 복잡하며, 위의 큐비트를 측정할 경우 $$|\alpha|^{2}$$의 확률로 0의 값을, $$|\beta|^{2}$$의 확률로 1의 값을 얻게 된다. 특별한 경우가 아닌 이상, 큐비트는 $$|\alpha|^{2} + |\beta|^{2}= 1$$을 만족하는 규격화된 형태로 주로 활용된다. 이는 $$|\alpha|^{2}$$와 $$|\beta|^{2}$$이 확률 값이므로 확률의 합이 1이 되는 규칙을 만족해야하기 때문이다. 규격화된 큐비트는 동일하게 다음과 같이 표현할 수 있다.

\[\cos\frac{\theta}{2}\left| 0\rangle \right. + e^{i\phi}\sin\frac{\theta}{2}\left| 1\rangle \right. \]

위와 같은 표현식에 따르면, 반지름이 1인 구에서 북극을 $$\left. |0 \right\rangle$$, 남극을 $$\left. |1 \right\rangle$$이라고 하면, 하나의 큐비트는 $$\theta$$를 극각, $$\varphi$$ 를 구면 좌표의 방위각으로 하는 구면 상의 한 점으로 이해할 수 있다. 이와 같은 표현방법에서 임의의 큐비트를 나타내는 반지름이 1인 구를 블로흐 구(Bloch sphere)라 한다.

중첩 원리, 얽힘 (Superposition Principle, Entanglement)

양자역학의 중첩 원리란 $$\left| a \right\rangle$$와 $$\left| b \right\rangle$$상태가 양자 물리계에 존재하는 상태일 경우 두 상태의 중첩인 $$\alpha\left| a \right\rangle + \beta\left| b \right\rangle$$ 또한 양자역학적으로 허용됨을 의미하는 양자역학의 기본 원리이다. 이 때, 각 상태에 존재할 확률의 합은 다음과 같이 1로 주어져야 한다. 즉 $$|\alpha|^{2} + |\beta|^{2}= 1$$ 이다. 양자 중첩은 고전 이론에서 기술하는 어떠한 현상과도 구분되는 양자물리학의 고유 성질 중 하나이다. 양자 중첩과 더불어 양자정보, 양자연산 분야에서 중요하게 활용되는 양자 현상 중 하나는 양자 상태의 얽힘이다. 예컨대 아래와 같은 이체(bipartite) 큐비트 상태를 가정하자.

\[\left| \psi \right\rangle= \frac{1}{\sqrt{2}} \left( |\left. 00 \right\rangle + |\left. 11 \right\rangle \right)\]

이 상태는 어떠한 경우에도 두 개의 단일 큐비트 상태의 텐서 곱 형태로 나타낼 수 없다. 즉, $$\left| \psi \right\rangle = \left| a \right\rangle\left| b \right\rangle$$와 같은 방식의 표현이 불가능하다. 이와 같은 양자 상태의 성질을 양자 얽힘이라 한다. 양자 얽힘은 벨 부등식의 위배, 양자 전송(quantum teleportation), 초압축 코딩(superdense coding), 양자 키 분배(quantum key distribution) 등 양자정보 프로토콜 전반에 걸쳐 핵심적인 역할을 하는 양자 상태의 성질이다. 대개의 경우에는 양자 얽힘이 존재하는지 여부를 벨 부등식을 위배하는지로 판별할 수 있지만 모든 경우에 그렇지는 않다. 대표적인 예로서, 얽힘을 가지고 있지만 벨 부등식을 위배하지는 않는 특정 변수 영역의 Werner 상태가 존재한다는 사실이 알려져 있다. 임의의 양자 상태에 대하여 얽힘 상태인지 판별하는 것은 수학적으로 어려운 문제이다. $$2 \otimes 3 차원$$ 이하의 힐베르트 공간에 존재하는 이체 상태(bipartite state)의 경우, Peres와 Horodecki에 의해, 주어진 양자 상태에 부분 전치(partial transpose)를 작용한 행렬이 양(positive)이 아니라는 것과 그 상태가 얽힘을 가지고 있다는 것이 서로 필요충분조건이 된다는 것이 증명되었다.

밀도 연산자 (Density Operator)

밀도 연산자는 임의의 양자 상태를 표현하는 양자 연산자로서 행렬 표현으로 나타낼 경우 밀도 행렬로 불리기도 한다. 밀도 연산자는 일반적으로 1차원 복소 벡터 형태로 표현되는 순수 상태와 구별되며, 이를 포함하는 일반적인 양자 상태 표현 방식이다. 보다 엄밀히 밀도 연산자 개념을 이해하기 위해서는 순수 상태의 앙상블이라는 개념이 필요하다. 어떤 물리계가 $$i$$로 구별되는 순수 상태 중 하나인 상태 $$\left| \psi_{i} \right\rangle$$에 존재할 확률이 $$p_{i}$$라 하자. 이 때, 모든 가능한 상태와 확률의 집합을 순수 상태의 앙상블이라 한다. 밀도 연산자 $$\rho$$는 앙상블이 정의될 때 다음과 같이 정의되는 물리량이다.

\[\rho= \sum_{i}^{}{p_{i}\left| \psi_{i} \right\rangle\left\langle \psi_{i} \right|}\]

역으로 밀도 연산자가 주어져 있을 때, 그 밀도 연산자의 순수 상태 앙상블 표현도 생각할 수 있다. 그러나 주어진 하나의 밀도 연산자의 순수 상태 앙상블 표현은 일반적으로 유일하지 않다.

밀도 연산자를 사용할 경우 주어진 상태의 유니타리(unitary) 변환이나 특정 측정값을 얻을 확률 등의 표기가 간단해지므로 양자정보이론에서 유용하게 활용된다. 밀도 연산자는 위와 같이 확률을 통해 정의되기 때문에, 그 정의로부터 다음과 같은 밀도 연산자의 기본 성질이 유도된다.

1. 밀도 연산자의 대각합(trace)은 1이다, $$\text{tr}\lbrack\rho\rbrack= 1$$.

2. 밀도 연산자는 양행렬(positive matrix)이다, $$\rho \geq 0.$$

3. 밀도 연산자는 에르미트(Hermitian) 행렬이다, $$\rho= \rho^{\dagger}$$.

결맞음 (Coherence)

결맞음은 간섭 상황에서 중요하게 고려되는 양자 상태의 성질이다. 순수 상태로 주어진 입사광선이 광분할기를 통과하는 상황을 고려하자. 분할된 전체 상태는 각각의 분리된 순수 상태 빛의 중첩으로 주어진다. 이때, 결맞음 상황에서 상태를 나타내는 밀도 행렬은 순수 상태 형태로 주어진다. 반면 결어긋남(decoherence) 상황에서 밀도 행렬은 혼합 상태 형태로 주어진다. 결맞음에 대한 이론은 역사적으로 양자광학 분야에서 주로 발전되었다. 결맞음 자체를 엄밀히 정량화하려는 노력은 비교적 근래에 이루어지고 있으며, 다양한 성과들이 보고되고 있다. Baumgratz, Cramer, Plenio가 제안한 결맞음 정량화 모델을 따르면, $$d$$차원에서 결어긋남 상태(decoherent state)는 임의의 $$p_{i}$$ 확률분포에 대해 $$\rho = \sum_{i = 1}^{d}{p_{i}\left| i \right\rangle\left\langle i \right|}$$와 같이 정의되며, 이를 제외한 모든 상태를 결맞음 상태로 정의한다.[1] 최근에는 결맞음과 얽힘 사이에 정량적 관계가 증명된 바 있다.[2] 특별히 양자광학에서 정의되는 ‘표준 결맞음 상태’는 고전 전자기파와 유사한 성질을 가지며, 최대 결맞음 성질을 보이므로 큰 중요성을 갖는다. 표준 결맞음 상태는 다음과 같이 Fock 상태의 중첩으로 정의된다.

\[\left| \alpha \right\rangle = \exp\left( - \frac{1}{2} |\alpha|^{2} \right)\sum_{n =0}^{\infty}\frac{\alpha^{n}}{(n!)^{1\text{/}2}} \left| n \right\rangle\]

이때, $$\alpha$$는 복소수이며, 결맞음 상태는 다음과 같이 소멸 연산자(annihilation operator), $$\widehat{a}$$의 고유상태가 되는 특성을 갖는다. 즉, $$\widehat{a}\left| \alpha \right\rangle=\alpha\left| \alpha \right\rangle$$이다. 이는 물리적으로, 결맞음 상태가 입자 소멸 과정에서 변화가 없음을 의미한다.

벨 부등식 (Bell Inequality)

벨 부등식은 (모든) 국소 실재론이 반드시 만족해야 하는 조건을 말한다. 벨 부등식의 충족 여부로 국소 실재론과 양자 이론을 판별한다.[3][4] 즉, 국소 실재론은 벨 부등식을 항상 만족하기 때문에, 어떤 실험 결과가 벨 부등식을 위배한다면 이는 국소 실재론이 아닌 양자 이론을 따른다는 것을 의미한다. 벨 부등식을 구성하는 요소는 일반적으로 상관관계에 관한 통계 기댓값(또는 확률)들이다. 상관관계(correlation)에 관한 통계 기댓값은 전체 측정 사건(event)의 결합 확률분포(joint probability distribution)이 결정한다. 따라서 전체 측정 사건에 대한 결합 확률분포를 알면 상관관계를 파악하거나 그 통계 기댓값을 구할 수 있다. 이를 가지고 벨 부등식 위배 여부를 조사한다.

벨 부등식 판별을 위한 시나리오는 다음과 같다. 여러 관찰자가 각자에게 주어진 여러 측정 중 하나를 무작위로 선택하여 측정을 수행한다. 이러한 시행을 반복한다. 충분히 많이 시행한 후, 관찰자들은 서로 모여서, 각자가 얻은 측정 결과값을 모아서 상관관계의 통계 기댓값(또는 확률)을 구하고, 벨 부등식 충족 여부를 조사한다. 예를 들어, 가장 단순한 상황은 두 명의 관찰자 Alice와 Bob이 각자에게 주어진 두 가지 측정 방식 중 하나를 무작위로 선택하여 수행하고, 측정 수행 결과로 얻는 측정값으로 두 가지 가능한 경우이다. 좀 더 구체적으로 살펴보면 다음과 같다. 각 관찰자에게 주어진 두 가지 측정 방식 중 Alice가 선택한 측정 방식을 $$x \in \text{\{}1,2\text{\}},$$ Bob이 선택한 측정 방식을 $$y \in \text{\{}1,2\text{\}}$$로 표기하고, Alice가 측정 후 얻은 측정 결과값을 $$a \in \text{\{} - 1,1\text{\}}$$, Bob의 측정 결과값은 $$b \in \text{\{} - 1,1\text{\}}$$로 표기하자. 이런 상황을 도식적으로 표현하면 아래 그림 1과 같다.

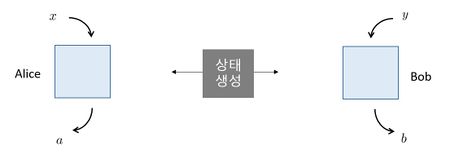
그림 1. 벨 시나리오 도식도. 상태생성기로부터 생성된 상태를 Alice와 Bob이 나누어 받은 후 Alice와 Bob은 각각 측정 $$x,y$$를 수행하여 각각 측정값 $$a,b$$를 얻는다.

위 그림 1은 가장 간단한 벨 시나리오 도식도이다. 이러한 상황에서 측정은 조건부 확률 $$p\left( ab \middle| xy \right)$$로 표현할 수 있다. 이 조건부 확률로 상관관계를 규명하거나 통계 기댓값을 구할 수 있다. 여러 번의 측정을 수행하면, 실험적으로 전체 측정 통계에 대한 실험적 근사치를 얻을 수 있다. 이는 상관관계 $$p\left( ab \middle| xy \right)$$가 실험적으로 측정 가능한 물리량임을 의미한다. 벨 부등식에 특정 상관관계를 대입하여 부등식을 만족한다면, 해당 상관관계는 국소 실재론을 통해 설명 가능하다는 의미에서 국소 상관관계라 할 수 있다. 반면 부등식을 만족하지 않는 상관관계는 비국소 상관관계라 하며, 이렇게 국소 실재론을 통하여 설명할 수 없는 상관관계의 성질을 ‘비국소성(non-locality)’이라 한다. 비국소성의 존재는 해당 물리계에 얽힘 상태가 존재함을 보장하기 때문에 이를 판별하는 벨 부등식은 얽힘 상태를 중요하게 활용하는 양자정보이론에서 중요한 의미를 갖는다. 더 나아가 비국소 상관관계가 물리계의 특성을 장치-독립 방식(device-independent scenario)으로 활용 가능함이 증명됨에 따라 양자 키 분배, 난수생성 등을 목적으로 하는 장치-독립 양자정보 프로토콜에서 비국소성의 응용 가능성 또한 주목받고 있다.

GHZ 상태 (Greenberger-Horne-Zeilinger State)

GHZ 상태란 3개 이상의 입자 사이의 높은 비고전성을 보여주는 양자 상태로서, 다체 물리계에서의 얽힘과 비국소성과 관련하여 많이 연구되어 왔다.[5] 다음과 같은 삼체(tripartite) GHZ 상태에 적절한 국소 측정을 수행하여, 최대 비국소성을 얻을 수 있음이 이른바 Mermin-GHZ 역설에 의해 알려져 있다.[6][5]

\[|\text{GHZ}\rangle=\frac{1}{\sqrt{2}}(|000\rangle+|111\rangle)\]

GHZ 상태에 국소성이 최대 위배되도록 제안된 Mermin-GHZ 상관관계는 순수 다체 비국소성(genuine multipartite non-locality) 성질이 없는 것으로 확인되었다.[7] Svetlichny에 의해 GHZ 상태를 활용하여 순수 다체 비국소성을 얻을 수 있으며[8], 더 나아가 Svetlichny 상관관계를 사용할 경우 양자역학에 의해 가능한 최대 위배를 얻을 수 있음이 확인되었다.[9] 삼체 GHZ 상태를 $$N$$개 입자, $$d$$차원 힐베르트 공간으로 일반화한 GHZ 상태는 다음과 같은 형태를 갖는다.

\[|\text{GHZ}_{N,d}\rangle=\frac{1}{\sqrt{d}}\sum_{i = 0}^{d - 1}\left| i \right\rangle^{\otimes N}\]

삼체 GHZ 상태에 대한 Mermin-GHZ 역설을 위의 일반화된 GHZ 상태에 대하여 일반화한 결과는 2000년대 초반까지 특정 개수의 입자와 특정 힐베르트 공간 차원에 대하여 제안되었으나[10] 2013년, 임의의 $$N, d$$에 대해 일반화한 결과가 보고되었다.[11] 임의의 $$N$$값에 대한 다체 GHZ 상태에 대하여 순수 다체 비국소성을 갖는 상관관계 또한 제안된 바 있다.[12][13][14]

고양이 상태 (Cat State)

슈뢰딩거(Schrödinger)가 처음 제안한 고양이 사고실험에서는 고양이가 살아 있는 상태와 죽어 있는 상태가 중첩되어 있는 상황을 고려한다. 이후 거시적으로 구분되는 두 상태가 중첩되어 있는 경우 이를 슈뢰딩거 고양이 역설에서 이름을 따와 고양이 상태라 부른다. 양자광학 분야에서 고양이 상태는 보다 엄밀히, 서로 반대되는 위상을 가진 결맞음 상태 2개의 중첩을 의미한다. 고전적으로 구분되는 두 개의 거시 상태를 중첩해서 얻은 양자 상태의 양자적 특성을 연구하기 위해 고양이 상태와 관련한 다양한 연구와 논의가 이루어지고 있다. 고양이 상태의 생성을 위해서는 주로 레이저의 결맞음 상태를 이용하는 방식이 사용된다. 이때 고양이 상태는 서로 다른 위상이나 진폭을 갖는 레이저 결맞음 상태의 중첩으로 주어진다. 고양이 상태의 실험적 구현을 위해서, 공동에 갇힌 마이크로파장의 광자를 이용한 방식이나[15], 공동에 갇힌 이온에서 방출하는 진동파를 이용한 방식이 제안된 바 있다.[16] 최근에는 광학 신호를 사용한 방법이 처음으로 제안되었다.[17] 해당 방법에서는 공진기에 갇힌 단일 루비듐 원자에 광학 신호를 입사하여 서로 반대되는 위상을 가진 신호의 중첩을 만들어 고양이 상태가 되도록 한다.

POVM (Positive Operator-Valued Measure)

양자 측정의 일반화된 표현으로서 POVM은 양자정보, 양자연산 분야에서 광범위하게 사용되는 측정 표현방식이다. POVM 측정은 완전성 관계 $$\sum_{m}^{}{ M_{m}}=I$$를 만족하는 양수 행렬들(positive matrices)의 집합이며, $$M_{m}$$은 POVM 요소(또는 원소, element)라 부른다. 주어진 양자 상태 상태 $$\left| \psi \right\rangle$$에 대해 POVM 요소와 측정값 $$m$$을 얻을 확률 $$p(m)$$ 사이의 관계는 다음과 같다. $$p(m)=\left\langle \psi \right|M_{m}\left| \psi \right\rangle$$. 이로부터, POVM 요소의 합이 연산자 $$I$$가 되는 것은 확률 합이 1이 되는 조건에 기인한다. POVM은 하나의 에르미트 연산자로 표현되는 투영측정(projective measurement)과 구분되며, POVM 방식이 투영측정 표현 방식을 포함한다. 하나의 투영측정 $$P$$가 있다고 가정하자. 이 때 투영측정은 에르미트 연산자로 표현되므로, 투영측정 $$P는$$ 측정값 $$m$$과, 이에 해당하는 투영자 $$P_{m}$$에 대하여 다음과 같은 고유값 분해 방식(eigenvalue decomposition, spectral decomposition)으로 표현가능하다. 즉, $$P=\sum_{m}^{}{mP_{m}}$$이고, $$\mspace{6mu}\sum_{m}^{}{ P_{m}}=I$$를 만족한다. 투영측정 표현방식에서 측정값 $$m$$을 얻을 확률은 다음과 같이 $$p(m)= \left\langle \psi \right|P_{m}^{\dagger}P_{m}\left| \psi \right\rangle$$로 주어진다. 따라서 제곱 연산에 대해 동일한 투영자 성질에 의해 투영측정 $$P$$는 항상 POVM 요소 $$M_{m} =P_{m}^{\dagger}P_{m}= P_{m}$$의 집합으로 표현가능함을 알 수 있다.[18] POVM 표현방식은 측정 상황을 편의적으로 기술하는 목적을 넘어 물리적인 중요성을 갖는 표현방식이다. 예컨대 POVM 측정을 사용하면 투영측정을 사용한 방식에 비해 더 높은 정도의 난수성 증명이 가능하다는 것이 최근 증명된 바 있다.[19]

참고 문헌

  1. ↑ T. Baumgratz, M. Cramer, and M. B. Plenio, Quantifying coherence, Physical Review Letters 113, 140401 (2014). doi:10.1103/PhysRevLett.113.140401. https://doi.org/10.1103/PhysRevLett.113.140401
  2. ↑ A. Streltsov et al., Measuring quantum coherence with entanglement, Physical Review Letters 115, 020403 (2015). doi:10.1103/PhysRevLett.115.020403. https://doi.org/10.1103/PhysRevLett.115.020403
  3. ↑ J. S. Bell, On the Einstein Podolsky Rosen paradox, Physics Physique Fizika 1, 195 (1964). doi:10.1103/PhysicsPhysiqueFizika.1.195. https://doi.org/10.1103/PhysicsPhysiqueFizika.1.195
  4. ↑ N. Brunner et al., Bell nonlocality, Reviews of Modern Physics, 86, 419 (2014). doi:10.1103/RevModPhys.86.419. https://doi.org/10.1103/RevModPhys.86.419
  5. ↑ 5.0 5.1 D. M. Greenberger, M. A. Horne, and A. Zeilinger, Going beyond Bell’s theorem in Bell's Theorem, Quantum Theory and Conceptions of the Universe (Springer, 1989). doi:10.1007/978-94-017-0849-4_10. https://doi.org/10.1007/978-94-017-0849-4_10
  6. ↑ N. D. Mermin, Extreme quantum entanglement in a superposition of macroscopically distinct states, Physical Review Letters 65, 1838 (1990). doi:10.1103/PhysRevLett.65.1838. https://doi.org/10.1103/PhysRevLett.65.1838
  7. ↑ J. L. Cereceda, Three-particle entanglement versus three-particle nonlocality, Physical Review A 66, 024102 (2002). doi:10.1103/PhysRevA.66.024102. https://doi.org/10.1103/PhysRevA.66.024102
  8. ↑ G. Svetlichny, Distinguishing three-body from two-body nonseparability by a Bell-type inequality, Physical Review D 35, 3066 (1987). doi:10.1103/PhysRevD.35.3066. https://doi.org/10.1103/PhysRevD.35.3066
  9. ↑ P. Mitchell, S. Popescu, and D. Roberts, Conditions for the confirmation of three-particle nonlocality, Physical Review A 70, 060101 (2004). doi:10.1103/PhysRevA.70.060101. https://doi.org/10.1103/PhysRevA.70.060101
  10. ↑ M. Żukowski and D. Kaszlikowski, Greenberger-Horne-Zeilinger paradoxes with symmetric multiport beam splitters, Physical Review A 59, 3200 (1999). doi:10.1103/PhysRevA.59.3200. https://doi.org/10.1103/PhysRevA.59.3200
  11. ↑ J. Ryu, C. Lee, M. Zukowski, and J. Lee, Greenberger-Horne-Zeilinger theorem for N qudits, Physical Review A 88, 042101 (2013). doi:10.1103/PhysRevA.88.042101. https://doi.org/10.1103/PhysRevA.88.042101
  12. ↑ D. Collins et al., Bell-type inequalities to detect true n-body nonseparability, Physical Review Letters 88, 170405 (2002). doi:10.1103/PhysRevLett.88.170405. https://doi.org/10.1103/PhysRevLett.88.170405
  13. ↑ M. Seevinck and G. Svetlichny, Bell-type inequalities for partial separability in N-particle systems and quantum mechanical violations, Physical Review Letters 89, 060401 (2002). doi:10.1103/PhysRevLett.89.060401. https://doi.org/10.1103/PhysRevLett.89.060401
  14. ↑ L. Aolita, R. Gallego, A. Cabello, and A. Acín, Fully nonlocal, monogamous, and random genuinely multipartite quantum correlations, Physical Review Letters 108, 100401 (2012). doi:10.1103/PhysRevLett.108.100401. https://doi.org/10.1103/PhysRevLett.108.100401
  15. ↑ S. Haroche, Controlling photons in a box and exploring the quantum to classical boundary, Annalen der Physik 525, 753 (2013). doi:10.1002/andp.201300737. https://doi.org/10.1002/andp.201300737
  16. ↑ D. J. Wineland, Nobel lecture: superposition, entanglement, and raising Schrödinger's cat, Reviews of Modern Physics 85, 1103 (2013). doi:10.1103/RevModPhys.85.1103. https://doi.org/10.1103/RevModPhys.85.1103
  17. ↑ B. Hacker et al, Deterministic creation of entangled atom–light Schrödinger-cat states, Nature Photonics 13, 110 (2019). doi:10.1038/s41566-018-0339-5. https://doi.org/10.1038/s41566-018-0339-5
  18. ↑ M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information (Cambridge University Press, 2002).
  19. ↑ A. Acín, S. Pironio, T. Vértesi, and P. Wittek, Optimal randomness certification from one entangled bit, Physical Review A 93, 040102 (2016). doi:10.1103/PhysRevA.93.040102. https://doi.org/10.1103/PhysRevA.93.040102
원본 주소 "https://wiki.qisk.or.kr/index.php?title=양자역학_개요&oldid=2047"